Egzamin dla Aktuariuszy z 2 czerwca 2008 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
P( sukces A) = ∫ P( sukces θ) f ( θ A), gdzie θ
A – w n próbach r sukcesów
f ( θ A) P( Aθ) f ( θ)
=
P( )
A
1 n
P( A) = ∫ P( Aθ) f θ
( ) = ∫
r
n− r
θ 1
( − θ)
θ
6 1
( − θ) dθ =
r
θ
0
n1
α = r + 2
n
=
r +1
n− r+1
( r
2) ( n
r
2)
6
∫
Γ + Γ − +
θ
1
( − θ)
=
=
6
r
β = n − r + 2
r
Γ( n + 4)
0
n r
n−
θ 1
(
r
− θ) 6 θ 1
( − θ)
r
n r
f ( θ A)
1
r
+
− +
θ
1
( − θ)
1 ( n + )
3 !
=
=
≅ B( r + ;
2 n − r + 2)
n Γ( r + 2)Γ( n − r + 2) ( r + )
1 !( n − r + )
1 !
6
r
Γ( n + 4)
1
r +2
θ
1
( −
n− r +1
θ)
( n + )
3 !
α = r +
ODP = ∫
3
( n + )
3 !( r + 2)!( n − r + ) 1 !
r +
=
=
=
2
( r + )
1 !( n − r + )
1 !
β = n − r + 2
( r + )
1 !( n − r + )
1 !( n + 4)!
n + 4
0
Zadanie 2
θ
θ
1
1
−
θ
<
< +
+
P(
P
X
t
t
X −1 < t X > )
1
(
)
1
2
2
2
1 =
=
= 1−
≅ Pareto( θ;2)
P( X > )
1
θ
t + 2
1
2
θ 2 θ
8
Y ≅
≅
i
(
H
Yi
+
2 + y
+
i )
p
rzy
:
0
θ 1
3
(2
y)
3
10
64
∏(2+ y
10
i )
8
P
H
>
0
t
P
t
H
5
10
0
10
∏(2 + y
8
i )
=
>
2
∏(2 + yi )
i=1
dla t ∈ ( ,
0 )
4
∞
8
8
8
θ
P
< t =
θ 2
P 2 + y
P y
y
x
i >
= i > − 2 =
∫
2
2 + y
t
t
θ 1
i
8
(2 + yi ) = + = =
+
3
2
1
−2
X i
t
∞
∞
θ
θ
θ
θ θ
θ
2
2
2 t
1
= ∫
= −
=
= t
θ +1
θ
θ
x
8
x 8
8
4
t
t
θ
1
θ 1
−
f =
t
θ
4
dla x
i ∈ ( ,
0 4)
t
θ
θ
1
1
P(
e
ln X
t
P X
e
x
θ
1
e
i <
) = ( < t
i
)= ∫
θ − = tθ
4
4
0
θ
1 tθ
f
t
( )
ln
= θ e
X i
4
θ
1
f
( t)
tθ
θ t
−
X
= θ −
e
d
l
a t ∈ (− ln ;
4 ∞
)
− ( +ln 4)
= e
θ ≅ wykl( θ;− ln 4) ln
i
4
β
0
x
α
(
4
6 4
78
− ln X
θ
i )
} }
∑
≅ Γ1 ;0 ;−10ln 4
ln
10
P(
− t
∏
θ
x
t
P
ln X
ln t
P
ln X
ln t
( x
9
10 ln 4) e ( 10ln 4) dx
i >
)= (∑ i > )= (−∑ i < − )= ∫
− θ x+
+
=
Γ
−
1
( 0)
10 ln 4
= x
w
θ
2
10 ln 4−ln t
2 θ 1
( 0 ln 4
10
−ln t)
10
9
− x
=
1
x + 10 ln 4 = w =
∫
θ
9 − θw
w e
dw =
= x
w
=
∫
θ
x
e 2
dx =
Γ 1
( 0)
θ
2
Γ
9
1
( 0) 2 θ 9
θ
2
0
0
= dx
dw
θ
2
2 θ 1
( 0 ln 4−ln t)
x
2 θ 1
( 0 ln 4−
−
ln t )
=
∫
1
9
x e
=
χ (2 )
0
0
,
0 5
10
∫ 2
2
=
2 Γ 1
(
)
0
0
0
4 1
( 0ln 4−ln t )
10 8
, 51
przy H :
∫
2
χ (20)
,
0 05
4 1
( 0 ln 4
ln t)
10 8
, 51
ln t
10 ln 4
0
=
→
−
=
→
=
−
4
0
10,851
8 10 ln 4−10 ln 4+
4
2 ,
1 702
x
x
−
t
2
1
9
=
czyli moc=
∫ χ (20) = ∫
2
x e
= 2
=
Γ
10
1
( 0)2
0
0
dx = 2 dt
10,851
10,851
= ∫
1
9 9 −
2
t
t e
⋅ dt =
1
2
t
t e
10
∫
9 −
Γ 1
( 0)2
Γ 1
( 0)
0
0
u = 9
t v′ = − t
e
u = 8
t v′ = − t
∫
e
9 − t
t e
=
= − 9 − t
t e
+ 8∫ 8 − t
t e
=
= − 9 − t
t e
+ ... =
u′ = 9 8
t v = − − t
e
u′ = 8 7
t v = − − t
e
= − 9 − t
t e
− 8 − t
t
9 e
− 9 ⋅ 7 − t
t
8 e
− 9 ⋅8⋅ 6 − t
t
7 e
− 9 ⋅8⋅ 7 ⋅ 5 − t
t
6 e
− 9 ⋅8⋅ 7 ⋅ 6 ⋅ 4 − t
t
5 e
−
− 9 ⋅⋅⋅ 3 −
2 −
−
−
t
4 e t − 9 ⋅ ⋅ ⋅ t
3 e t − 9 ⋅ ⋅ ⋅ t
2 e t − !
9 e t 10,851
0
= X
= X
ODP
≈ ,
0 643
!
9
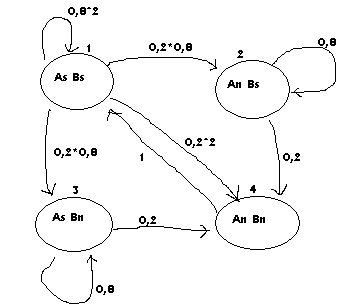
Zadanie 3
,
0 64
1
,
0 6
1
,
0 6
,
0 04
0
8
,
0
0
,
0 2
szukamy rozkł. Stacjonarnego i ODP= p + p 0
0
8
,
0
,
0 2
2
3
1
0
0
0
,
0 64 p
p
p
1 +
4 =
1
p
36
,
0
p
4 =
16
,
0
p
8
,
0 p
p
1 +
2 =
2
1
→ p
8
,
0 p
2 =
1
16
,
0
p
8
,
0 p
p
1 +
3 =
3
p
8
,
0 p
3 =
1
,
0 04 p
,
0 2 p
,
0 2 p
p
1 +
2 +
3 =
4
p + p + p + p = 1
1
2
3
4
p + 8
,
0 p + 8
,
0 p + 3
,
0 6 p = 1
1
1
1
1
1
8
,
0
8
,
0
p =
, p =
, p =
1
3
2
9
,
2 6
9
,
2 6
9
,
2 6
8
,
0 + 8
,
0
ODP =
≈ 5
,
0 41
9
,
2 6
Zadanie 4
∑( X
i − X )2 =
2
2
σ χ ( n − )
1
2
σ
X ≅ N m;
n
2
a∑ ( X
2
i − X ) +
X
b
= T
szukamy a,b
2
2
E( T ) = m + σ = E( 2
X
1 )
σ 2
2
2
2
2
1
aσ ( n − )
1 + b
+ m = m + σ → b = , 1 a =
n
n
T = 1 ∑ ( X
i − X )2 +
2
X
n
wiemy, Ŝe (∑ X 2;
X - dostateczna, zupełna
i
∑ i )
E( T ∑ 2
X ,
- ENMW
i
∑ Xi ) 1
2
czyli
= ∑( Xi − X ) + 2
X
n
szukamy var(T)
1
σ
n −
σ
σ
var
∑( X − X =
=
−
i
)
4
4
4
2
2
(
)
1
2
2
2
2
n
n
n
n
2
4
var X
= EX − ( EX )2
2
2
σ
X − m ≅ N ;
0
n
E( X − m)
4
4
σ
σ
= 3
= E X − 4 X m + 6 X m − 4 Xm + m = EX − 4 m X
E
+ 6 m
+ m − 4 m + m
2
( 4
3
2
2
3
4 )
2
4
3
2
2
4
4
n
n
σ
0 = E( X − m)3 = E( 3
2
2
3
X − 3 X m + 3 Xm − m ) 2
3
2
3
3
= X
E
− 3 m
+ m + 3 m − m
n
2
2
3
3 σ
m
3
3
3
3 σ
m
3
EX
=
+ 3 m − 3 m + m =
+ m
n
n
4
2
2
2
4
3 σ
3 σ
m
3
EX
=
+
m σ
4 m
+ m − 6
−
4
6 m +
4
4 m −
4
m =
2
n
n
n
4
2
2
2
2
4
2
2
3 σ
12 m σ
4
6 m σ
4
4
4
3 σ
6 m σ
4
=
+
+ 4 m −
− 6 m + 4 m − m =
+
+ m
2
2
n
n
n
n
n
4
4
4
2
2
2
2
4
4
4
2
2
2 σ
2 σ
3 σ
6 m σ
4
σ
2
ODP =
−
+
+
+ m −
+
= 2 σ
m
− 2 σ + 3 σ + 6 m σ + 4
m −
2
2
n
n
n
n
n
2
2
n
n
n
n
4
2
2
4
2
2
2
σ
2 σ m
4
2 σ
4 m σ
2 σ
−
−
− m =
+
=
2 m + σ
2
( 2 2)
n
n
n
n
n
Zadanie 5
m = E( e X ) g
dzi
e X ≅ N (
2
;
µ σ )
1 2
µ+ σ
2
m = e
dla danych:
0,5
m = e
d
2
2
2
σ
z teorii wiemy, Ŝe dla ENW w lognormalnym
T
;
1
/
n − m → N m m σ +
n
2
σ 2
2
e
3
σ
m
1
+
/ n =
n
2 n
( Tn − m) n 2 d
2 2 2
czyli
→ N(
c
)
1
,
0
zyl
i
ODP = P X >
g
, dzie X
≅ N(0,1)
3 e
3 e
4
czyli
P X >
→ ODP = 1
,
0 6152
{
3 e
≈ ,
1 4
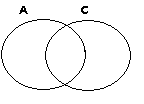
Zadanie 6
P( )
A − P( A ∩ C) > 0
P( C) − P( A ∩ C) > 0
z załoŜeń wynika, Ŝe tak musi być jak na rysunku
∩
∪
∩
∩
+
∩
−
∩ ∩
∩
P( B A ∪ C) P ( B
A) ( B
C )
P( A
B) P( B
C ) P( A
B
C )
P( B
C )
=
=
>
P( A ∪ C)
P( A ∪ C)
P( C)
P( B A − C) P( A − C) + P( B ∩ C) P( B ∩ C)
L =
>
P( A ∪ C)
P( C)
P( B ∩ C) P( A∪ C)− P( B ∩ C) P( B ∩ C)( P( A) + P C
( ) − P( A ∩ C) − P( B ∩ C) ( )
( )
P( B A − C) >
P C
=
P C
P( A − C)
P( A) − P( A
C )
=
∩
∩
P( B ∩ C) P( B
C )
+
( P( A) − P( A∩ C) − P( B ∩ C) P C
( )
P( B ∩ C)
=
=
=
→
P( A) − P( A ∩ C) P( B C)
C
P C
( )
prawidłowa
Zadanie 7
cov( N
N
N
N
N
b +
,
z
r +
z −
cz ) = 0
to są rozkłady Bernoulliego
cov( N , N
b
r )
1
50
14
54
18
=
−
−
= −
2 225
225
225
450
2
2
k
k
k
k
k
k
k
k
k
k
cov( N , N
b
z )
1 (6 − ) 9
( + )
14
5
( − ) 1
( 0 + )
1 54 + 6 − 9 −
−14 − 50 − 5 +10 +
=
−
−
=
=
2
225
225
225
2
225
1 2 k −10
2 k − 10
=
=
2
225
450
2
2
k +
− k
k
− k
k − k +
− k − − k + k
k
k
cov( N , N
=
−
−
=
= −
= −
b
cz )
1 (
)
1 1
( 4
)
14
1
( 5
)
1 14
14
14 15
2
2
225
225
225
2
225
450
225
2
2
k k
k
k
k
k
k
k
k
k
cov( N , N
z
r )
1 1
( 4 − )( + )
1
5
( − ) 1
( 0 + )
54
1 14 + 14 −
− − 50 − 5 +10 +
−
=
54
−
−
=
=
2
225
225
225
2
225
1 18 k − 90
18 k − 90
=
=
2
225
450
5
( − k) 1
( 0 + k)
50 − 5
2
k − k
var N =
=
z
225
225
2
2
2
− k
+ k
k
− k
−
− k + k + k − k + k k −
k
cov( N , N
=
−
−
=
=
z
cz )
1
50
5
(
) 1
( 0
)
1
( 5
)
1 50
50
5
10
15
2
10
2 225
225
225
2
225
450
18
2 k −10
k
18 k − 90
50 − 5 k − 2
k
2 2
k −
−
+
+
+
+
−
10 k = 0 →
450
450
225
450
225
450
→ −18 + 2 k −10 + 2 k +18 k − 90 +100 −10 k − 2 2
k − 2 2
k + 10 k = 0
4 2
k − 22 k + 18 = 0 → k = 1
Zadanie 8
Dla t ∈ ( z )
1
;
P(
n−
n−
M < t X = z = P
( X < t) = t
1
)
1
2(
)
1
f (
n−
M X = z = (2 n − 2) t 1
)
2
3
P(
1
M = z X
z
1 P M
( z )
1
; X
z
1
(2 n
2) n
t
1
1
n
n
z
z
1 =
)= − ( ∈
1 =
)= − ∫
2 −
−
3 = − (
2 −
−
2 )
2 −
=
2
z
E(
1
n
n
2 n
2
2 n
2
M X
z
(2 n
2)
n
n
t
dt
z z
z
z
1 =
)= ∫
2 −2
2 −2
−
−
−
+ ⋅
=
−
2 −1 + 2 −1 =
2 n −1
2 n −1
z
n−
n−
2 n − 2 − (2 n − 2 − 2 n + ) 1 2 1
z
2 n − 2
2
1
+
=
=
z
2 n −1
2 n −1
Zadanie 9
E( S λ)
1
= λ ⋅ = 1
λ
E( T λ)
2
= λ ⋅ = 2
λ
cov( E( S λ), E( T λ) = 0
cov( S, T ) = cov( E( S λ), E( T λ) + E(cov( S, T λ) = E(cov( S, T λ) cov( S, T λ) = (var( S + T λ)− var( S λ)− var( T λ) ⋅ 5
,
0
=
= [ λ( E( 2
X
λ)+ E( 2
Y λ)+ 2 E( X λ) E( Y λ) − λE( 2
X
λ)− λE( 2
Y λ)]⋅ 5
,
0
=
2
8
1 2
2
8
14
2
8
2
= λ
+
+ 2 ⋅ ⋅ − λ
− λ
5
,
0
=
− − 5
,
0
=
λ 2
λ 2
λ λ
λ 2
λ 2
λ
λ
λ
λ
∞
∞
2
2 8
λ
16
α =
cov( S, T ) =
3
λ
16
)
3
(
16 2
4
E = ∫
3 −2
λ e
=
∫ 2 −2
Γ
λ e
=
=
=
=
λ
λ 3
3
β =
3
3
2
3 2
3 2
3
0
0
var S = var( E( S λ) + E(var( S λ) 1
2
2
4
= var λ ⋅ + E λ = E =
2
λ
λ
λ
3
var T = var( E( T λ) + E(var( T λ) 2
2
8
16
= var λ + E λ
⋅ 4 = E =
2
λ
λ
λ
3
4
4 3
1
3
corr( S, T ) =
=
=
4 16
3 2 ⋅ 4
2
3
3
Zadanie 10
Przy H :
0
X − Y ≅ N
i
i
( 2
;
0 2 σ )
X − Y = X − Y
X
stąd szukamy c by: P
> c = ,
0 05 g
dzi
e X ≅ N
( 2
;
0 2 σ )
1
2
∑ X
i
10
2
2
X
X
2
X
2
P
> c = P
> c = P
> c =
2
S
1
S
2
∑ X
i
10
1
2
∑( Xi − X )2
+ 2
X
X
2
1
10
= P
> c = P
<
=
2
2
1
∑( Xi − X )2
2
+ X
X
c
10
1
∑( Xi − X )
2
2
2
1
X
c
2
X
c
10
= P
<
−1 = P
>
= PH
>
=
2
2
X
c
1
2
1 − 2
0
2
∑( Xi − X )
c
1
2
1 −
c
∑( Xi − X )
10
10
2
2
c
=
c
P T
)
9
(
>
9 =
0
,
0 5 → 3
= ,
2 262
1
2
− c
1
2
−
c
2
2
c
,
2 262
=
2
1 − c
3
2
,
2 262
3
c =
≈ ,
0 602
2
,
2 262
1 +
3