Egzamin dla Aktuariuszy z 12 stycznia 2002 r.
Prawdopodobieństwo i Statystyka Zadanie 1
X
n+ = X n ⋅ X X ≅ J (
)
1
,
0
X n − iloczyn n X
≅ J(0,1)
1
Z tego:
n
1
EX =
n
2
1
2
1
1
1
EX 2 = ( EX 2 ) n
n = EX =
+ =
n
3
12
4
3
n
2 n
1
1
var X = −
n
3
2
2
n
n
n
n
1
4
1
1
−1
−
2
3
3
4
n
4
ODP =
=
= −1
n
n
3
1
1
2
2
Zadanie 2
Metodą eliminacji dla N
A = 2
E( N N
E A N
P A
N
P A
N
1
A = 2) = 6 +
( 1 A = 2)= 6+1⋅ ( 1=1 A = 2)+ 2 ( 1= 2 A = 2)=
8
4
8
8
8
1
1
8
2
8
8 ⋅ 4 + 2 ⋅ 28
1
= 6 +1
+ 2
= 6 +
= 7 i pasuje tylko odpowiedź (E)
12
12
66
3
2
2
moŜna policzyć EN
i
EN i sprawdzić czy EE( N N
= EN
1
A )
1
A
1
Zadanie 3
2
X
var( Y X ) ≤
4
1
1
2
X
var X +
E ( X ) = var
+ E(var( Y X ) =
2
4
2
1
1
var X +
E 2 ( X ) = E(var( Y X ) 4
4
jesli
2
1
2
EX
= E(
X
var( Y X )
< E
= 1
2
EX
→
sprzeczność
4
4
4
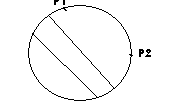
2
X
Z tego var( Y X ) =
a skoro tak to:
4
P( Y = X )= 1
0
2
1
P( Y = X X ) =
2
P( Y = x) = ∫ P( Y = x x) f ( x = ∫ 1
)
f ( x = 1
)
2
2
Zadanie 4
A
- nie przetną się
P( A P
x
P P
x
P
x
P
x P
x
2 =
)= ( 3 ∈( , Π
2 ), 4 ∈ ( , Π
2
l
) u
b 3 ∈ ( ,
0 ), 4 ∈ ( ,
0 )) =
2
2
2Π
x
2
2
2
2
2
2
1
1
2Π − x
x
(2Π) − 4Π x + x +
= ∫
+ ∫
=
x
x
x
+
=
= 1−
+
2
2
2Π
2Π
2Π
2Π
(2
x
Π)
Π 2Π
0
2
x
x
2Π 1 −
+
P( )
A = ∫
Π 2Π2 =1− + 2
1
= 2
2Π
3
3
0
2
1
ODP = 1 −
=
3
3
Zadanie 5
E( ˆ
W − W )2 = E( zX
1
(
z) X
X
pX
E ( z
)
1 X
1
(
z
p) X
1 +
−
0 −
1 +
)2
0
= ( −
1 +
− +
)2
0
=
= E[( z − 2 2
)
1 X
(
2 z
)
1 1
(
z
p) X X
1
(
z
p) X
1 +
−
− +
0
1 +
− + 2 20 ]=
= ( 2
z − 2 z + )
2
1 EX
4 z
2 z
2 zp
2
2 p E X X
1 2 z
z
2 p
2 pz
p EX
1 + (
− 2 +
− −
) ( 0 )+( − + 2
1
+
−
+ 2 ) 20 =
>0
6
4
4
4
4
7
4
4
4
4
8
= z 2 EX 2 2
2
4
2
2
2
1 −
E
2
2
2
2
( X X
0
1 ) + EX 0 + z(−
EX 1 + E( X X
0
1 ) +
pE( X X
0
1 ) −
EX 0 − pEX 0 )+ c
2
2
b
2 EX + 2 EX 1
( + p) − 2 E X X (2 + p) 0
1
( 0 1)
z = −
=
*
2
2 a
2 EX − 4 E X X
+ 2 EX
1
( 0 1)
2
0
EX 2
1
0 =
EX 2
1
1 =
E( X X
cov
,
0
1 ) =
( X X
0
1 ) = p
2 + 2 1
( + p) − 2 p(2 + p) 2 + 2 + 2 p − 4 − 2 2
p
2( p + 2) − 2 p( p + 2) 2( p + 2) 1
( − p)
p
z =
=
=
=
= 1+
*
2 − 4 p + 2
4 1
( − p)
4 1
( − p)
4 1
( − p)
2
Zadanie 6
n
p
1
2
2
3
1
3
⋅ 2
2
..
..
ORR
OROO
ROROO
k
1
−
k
1
1
k
⋅ 2 =
ROO
RORR
ORORR
2
2
∞
k −1
2
X = ODP = ∑ 1
1
1
k
= 2 ⋅ +
3
+ ...
k =
2
2
2
2
2
3
1
1
1
X
= 2 + 3 + ...
2
2
2
2
1
2
3
1
1
1
1
2
1
3
X 1 − = 2 ⋅
+ + + ... = 1+
= 1+ ⋅ 2 =
2
2
2
2
1
4
2
1 − 2
3
X =
⋅ 2 = 3
2
Zadanie 7
2
σ
X ≅ N µ,
n
2
σ
X = Y + µ, Y ≅ N , 0
n
4
X
E
= E( 4
3
2
2
2
2
3
4
σ
µ σ
Y + 4 Y
µ
+ 4 µ Y + 2 Y µ + 4 µ Y + µ ) 4
2
2
3
6
4
=
+
+ µ
2
n
n
∑( X − X
i
)2
2
2
E
= n −1 → ES = σ
2
σ
2
2
2
2
4
4
2
S
4
2 S X
S
µ
E
= E X −
=
E X −
+
2
n
n
n
E( 2 2
S X )
2
2
2
2 σ
2
= ES X
E
= σ
+ µ
n
2
S ( n − )
1
4
S ( n − )
1 2
≅ χ( n − )
1
→ E
= 2( n − )
1 + ( n − )
1 2
2
= n −1
2
4
σ
σ
4
4
σ
σ
n +
4
(
)
1
ES =
( n − )
1 ( n + )
1 =
( n − )
1 2
n −1
4
2
2
4
4
3 σ
6 µ σ
4
2 σ
2
2
1 σ ( n + ) 1
var =
+
+ µ −
+ σ µ +
− 4
µ =
2
2
n
n
n n
n
n −1
3 4
σ
6 2 2
µ σ
2 4
σ
2 2 2
4
σ µ
σ ( n + )
1
4
σ
4 2 2
4
µ σ
σ ( n +
=
+
−
−
+
=
+
+
)
1 =
2
2
2
n
n
n
n
n ( n − )
1
2
2
n
n
n ( n − )
1
4
4
4
( n − )
1 σ + σ ( n + ) 1
4 2 2
2 nσ
4 2 2
2
4
4 2 2
=
+ µ σ =
+ µ σ =
σ +
µ σ
2
2
n ( n − )
1
n
n ( n − )
1
n
n( n − )
1
n
Zadanie 8
Innymi słowami: znaleźć n takie by test najmocniejszy istniał
n
∑( X 1
i − 0
)1
, 2
1 −
2
e
2Π
ln t + ,
1 005 n
P
> t = P ∑ X
i >
=
0
n
∑( X 1
i − 0)
,
0 05
2
0
1
,
0
1
−
2
e
2Π
ln t + ,
1 005 n
−10 n
∑ X −10 n
+
i
1
,
0
ln t
,
1 005 n
= P
>
= ,
0 05 →= ,
1 64 →
= ,
1 64 n + 10 n
0
n
n
1
,
0
∑ X i −10 1, n
,
1 64 n + 10 n −10 1
,
n
moc:
P
>
≥ 5
,
0
→ ,
1 64 + 10 n −10 1
,
n ≤ 0
n
n
1
,
0
n ≥ ,
1 64
n ≥ 1 ,
6 4
n ≥ 268 9
, 6 ≈ 271
Zadanie 9
S: c-kwantyl rzędu 0,01 z chi(5), z tego c=0,554
2
2
3
2
S
S
X
X
X
N : G
= 2
2
123
1
, G
, S
X
123
456 =
456
2
123 =
∑
1 +
2 +
i −
3
,
0 211
,
0 211
2 i=
3
1
6
2
2
1
X
X
X
S
X
456 =
∑
4 +
5 +
i −
6
2 i=
3
4
2 2
2
S
S
n
zl o
d 2
S
123
χ
123
456
≅ ( )
2 ≅
2
σ
5 2
S
5 2
σ
5 2
EG
S = E
=
S
b
o
E
= 5
5
,
0 54
5
,
0 54
2
σ
2
G
N =
2
σ
max( 2
2
S
S
X
X
X
χ
123
456 ) =
2
,
max(
,
1
2 )
1
n
z
l (2)
i
≅ wyk l
,
0 211
,
0 211 2
2
σ 2
3
σ
3 2
3
5
,
0 54
EG
=
⋅ 2 =
=
E G
≈ 5
,
1 8 E G
N
( S )
( S )
,
0 211 2
,
0 211
,
0 211
5
Zadanie 10
2
var S = λEX
2
var S = λ X
E
2
2
EX
=
2
λ
1
EX =
λ
∞
2
∞
a
− λ t+
∞
2
X
E 2 = ∫
a
−
a
x −
λx
λe
dx = x −
= t = ∫ 2
λ
−
t λe
dt =
a
e
∫ 2 − λt
−
t λe
= a
e
λ
λ
2
a
λ
0
0
λ
−
e a
S = 2
var
λ
−
2
2 e a
2
var S =
→
= 3
,
0 6
→ − a = ln 3
,
0 6 → a = − ln 3
,
0 6 ≈ ,
1 0217
λ
λ
λ