Rezystancja wejściowa wzmacniacza operacyjnego Michał Urbański

1

Rezystancja wejściowa wzmac-2

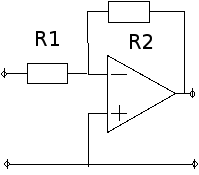
Rezystancja wejściowa wzmacniacza odwracającego fazę

niacza nieodwracającego fazy I

I

2

d

+

I

R

w

U

R

2

I

d

d

1

R

R

w

I

I

I

1

2

w y j

w e j

-

-

U

I

2

w

I

R

d

-AU

2

d

I

U

R

1

w

U

1

1

U

R

d

U

d

2

+

R

E=AU

1

d

Sterowana siła elektromotoryczna E = −AUd (znak −

wynika z tego, że strzałka jest przy wejściu ”−”).

Z praw Kirchoffa:

Rw – rezystancja wewnętrzna wzmacniacza operacyj-U1 = IdRd + I1R1

(10)

nego bez sprzężenia zwrotnego.

I

Z praw Kirchoffa:

2 = I1 = Id

(11)

AUd = I1R1 + I2R2 − IwRw

(12)

U1 = IwejR1 + Ud

(1)

−

Zakładamy jak poprzednio, że I AU

wyj = 0, więc Iw = −I2,

d + Iw Rw = I1R2 + IdRd

(2)

ponadto Ud = IdRd, po podstawieniu do (12) otrzymu-I1 + Iwej = Id

(3)

jemy:

Ud = IdRd

(4)

AIdRd = I1R1 + (R2 + Rw)I1 − (R2 + Rw)Id (13)

Jeśli założymy, że I2 = 0 (układ pracuje bez obciążenia) (14)

to Iw = −I1, wstawiamy to do równania (2): a z tego:

−AUd = (R2 + Rw)I1 + IdRd

(5)

ARd + R2 + Rw

z równania (3) mamy I

I

(15)

1 = Id − Iwej . Wstawiamy to

1 = Id R1 + R2 + Rw

do (5) i uwzględniając (4) otrzymujemy: wstawiamy (15) do (10):

−AIdRd = (R2 + Rw)Id − (R2 + Rw)Iwej + IdRd (6) U1

ARd + R2 + Rw

R

= R

(16)

i po przekształceniach:

wej =

d +

Id

R1 + R2 + Rw

Id

R2 + Rw

R2

Przy założeniu, że R

=

≈

(7)

w R2 oraz ARd R2 + Rw :

Iwej

ARd + R2 + Rw + Rd

ARd

R2

R

(17)

Przybliżony wzór uzyskujemy przy założeniu, że wej ≈ ARd R2 + R1

Rw R2 oraz ARd R2 + Rw + Rd.

Wzór (16) można zapisać następująco: Dzieląc U1 z równania (1) przez prąd Iwej otrzymu-

jemy rezystancję wejściową:

R2

A

Rwej = Rd 1 + A

= Rd 1 +

(18)

U

R1 + R2

Ku

1

Id

R2

Rwej =

= R1 +

Rd = R1 +

≈ R1

(8)

I

R

wej

Iwej

A

1 + R2

gdzie Ku =

.

Rezystancja wejściowa wzmacniacza odwracającego R2

Wzór (17) można wyprowadzić w sposób przybliżony fazę nie zależy praktycznie od sprzężenia zwrotnego bo-następująco:

wiem Ud IwejR1.

Wzór (8) można zapisać następująco:

∆U1

∆U1 ∆U2 ∆Ud

1

Rwej =

≈

=

ARd

(19)

∆I

∆U ∆U ∆I

K

R

d

2

d

d

u

2

Ku

Rwej = R1 1 +

= R1 1 +

(9)

Przy czym założono, że ∆E = ∆U

AR

2.

1

A

Jak widać wzmacniacz nieodwracający fazy ma dużą R2

gdzie: K

impedancję wynikającą ze sprzężenia zwrotnego. W

u =

. Czyli sprzężenie zwrotne zmniejsza R1

przypadku wzmacniacza odwracającego fazę sprzężenie wpływ R2.

zwrotne nie wpływa na rezystancję wejściową i rezystancja wejściowa równa jest rezystancji rezystora wejścio-wego R1.

1