Blok 5: Układy nieinercjalne.

Siły bezwładności

ZESTAW ZADAŃ NA ZAJĘCIA

Uwaga: w poniższych zadaniach przyjmij, że wartość przyspieszenia ziemskiego jest równa r

2

| g |= 10 m / s .

SIŁA BEZWŁADNOŚCI W RUCHU POSTĘPOWYM

1. Narysuj siły działające na pasażera windy szybkobieżnej poruszającej się pionowo w górę z r

przyspieszeniem a o wartości a < g .

2. Człowiek stojący na wadze sprężynowej w poruszającej się windzie zauważa, że waga wskazuje ¾ jego ciężaru wyznaczanego na wadze sprężynowej w windzie spoczywającej

względem Ziemi. Na tej podstawie można wywnioskować, że winda porusza się ruchem

(wybierz wszystkie poprawne odpowiedzi):

A) jednostajnie przyspieszonym w górę

B) jednostajnie opóźnionym w dół

C) jednostajnie opóźnionym w górę

D) jednostajnie przyspieszonym w dół

E) jednostajnym w górę

F) jednostajnym w dół

3. Wiadro napełnione wodą, z otworami w dnie oraz w ścianie bocznej spada swobodnie w dół.

Zakładamy, że opory powietrza są pomijalne. Wybierz jedną z poniższych możliwości

(i uzasadnij). Podczas spadania:

A) woda wylewa się z wiadra

B) woda nie wylewa się z wiadra

C) woda wylewa się tylko bocznym otworem

D) woda wylewa się tylko otworem w dnie

4. Na poziomej desce o masie M położono klocek o masie

m. Oblicz wartość przyspieszenia a, z jakim może

poruszać się poziomo deska, aby klocek spoczywał

względem niej. Znany jest współczynnik tarcia statycznego µ pomiędzy klockiem i deską oraz wartość przyspieszenia ziemskiego g.

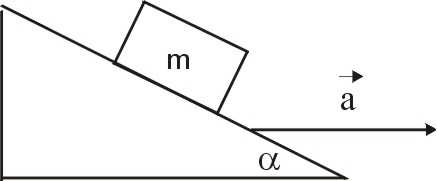
5. Klocek może zsuwać się bez tarcia z równi pochyłej o kącie r

nachylenia α . Jeżeli równia porusza się z przyspieszeniem a w

kierunku poziomym, to ciało nie zsuwa się. Ile wynosi wartość

przyspieszenia?

6. Nić wahadła zawieszonego u sufitu wagonu jest odchylona od pionu o stały kąt przeciwnie do ruchu wagonu. Jeżeli wagon porusza się po torze poziomym, to możemy wnioskować, że jedzie on ruchem:

A) jednostajnie przyspieszonym po linii prostej lub ruchem jednostajnym po okręgu

B) jednostajnie przyspieszonym po linii prostej

C) niejednostajnie przyspieszonym, przy czym wartość przyspieszenia wzrasta równomiernie D) jednostajnie opóźnionym po linii prostej lub ruchem jednostajnym po okręgu

E) jednostajnie opóźnionym po linii prostej

1

F) niejednostajnie opóźnionym, przy czym wartość przyspieszenia wzrasta równomiernie G) jednostajnie przyspieszonym lub jednostajnie opóźnionym po linii prostej

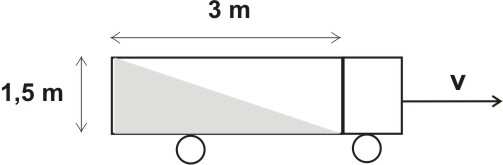
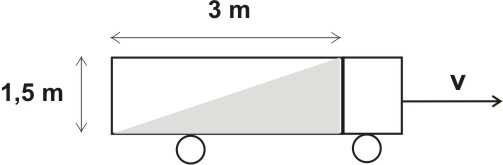
7. Cysterna wypełniona do połowy wodą pitną jedzie po prostej drodze. W chwili, gdy kierowca gwałtownie przyspieszył, woda przyjęła położenie przedstawione na jednym z rysunków:

• Wybierz rysunek poprawnie przedstawiający opisaną sytuację

• Oblicz wartość a przyspieszenia, z jakim poruszała się cysterna

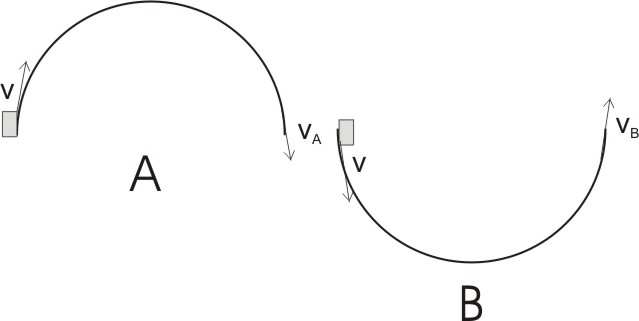
8. Dwa jednakowe ciała A i B ruszyły z szybkością v po dwóch torach o takich samych kształtach w płaszczyźnie pionowej. Jeżeli współczynnik tarcia kinetycznego pomiędzy ciałami, a torami jest równy µ > 0 , to wartości prędkości, z

jakimi ciała opuszczą tory, spełniają

warunek:

A) v

= v ≠ v

A

B

B) v

>

A

v B

C) v

<

A

v B

D) v

= v = v

A

B

SIŁA ODŚRODKOWA

9. Określ kierunek i zwrot siły wypadkowej działającej na punkt materialny poruszający się ruchem jednostajnym po okręgu. Zadanie rozwiąż w układzie laboratoryjnym oraz w układzie związanym z wymienionym punktem materialnym.

10. Na brzegu obracającej się płyty gramofonowej leży klocek. Współczynnik tarcia statycznego pomiędzy klockiem a płytą wynosi µs , współczynnik tarcia kinetycznego pomiędzy klockiem a płytą wynosi µk , średnica płyty wynosi D. Przy jakiej najmniejszej liczbie n obrotów na sekundę klocek spadnie z tarczy?

11. Rowerzysta wjeżdża w zakręt o promieniu krzywizny r = 50 m z szybkością 36 km/h. Pod jakim kątem do poziomu i w którą stronę powinien się nachylić, aby bezpiecznie przejechać zakręt (tzn. nie przewrócić roweru na bok) ?

12. Z jaką szybkością kątową powinno poruszać się wiadro po okręgu o promieniu r, w płaszczyźnie pionowej, aby nie wylała się z niego woda (otwór wiadra zwrócony jest stale do środka okręgu)?

13. Kulka o masie m=5g przywiązana do nitki o długości L = 45 cm wiruje w płaszczyźnie poziomej (wahadło stożkowe). Nitka jest nieważka i nierozciągliwa i tworzy z pionem kąt

o

α = 30 .

• Narysuj siły działające na kilkę w układzie inercjalnym oraz siły działające

na kulkę w układzie nieinercjalnym.

• Oblicz czas, w którym kulka zakreśla jeden okrąg.

• Oblicz wartość siły napięcia nici.

14. Wahadło matematyczne. Wyjaśnij, czy siła napięcia nici wahadła matematycznego drgającego w płaszczyźnie pionowej jest stała co do wartości, czy też zmienia się.

2

ZESTAW ZADAŃ DO SAMODZIELNEGO ROZWIĄZANIA

1. Uwaga: w tym zadaniu wybierz wszystkie poprawne stwierdzenia.

W szybkobieżnej windzie na wadze sprężynowej stoi człowiek o masie 80 kg . Wskazanie wagi wynosi 1000 N. Winda porusza się:

A) w dół przyspieszając

B) do góry przyspieszając

C) w dół hamując

D) do góry hamując

2. W windzie na wadze sprężynowej leży masa m = 100 kg . Jakie jest wskazanie wagi, jeśli winda urwała się i spada swobodnie? Odpowiedź uzasadnij.

3. Co dzieje się z wahadłem matematycznym zawieszonym u sufitu autobusu, który rusza z przystanku z przyspieszeniem o stałej wartości a – czy nić natychmiast ustawia się pod odpowiednim kątem α do pionu, czy też trwa to przez jakiś czas? Co się dzieje wówczas z wartością siły naciągu nici? Pod jakim kątem do pionu ustawi się ostatecznie nić wahadła –

narysuj odpowiedni rysunek i napisz prawidłowy wzór.

4. Pod jakim kątem względem poziomu powinien nachylić się człowiek stojący w autobusie, aby nie upaść, jeżeli autobus rusza z przyspieszeniem a = g 3 / 3 ?

5. Samolot wykonuje pionową pętlę w kształcie okręgu o promieniu 200 m. W najniższym i najwyższym punkcie toru szybkość samolotu wynosi 100 m/s. Jeżeli przyjmiemy, że masa

pilota wynosi 80 kg, to jaki jest nacisk pilota na fotel w najniższym i najwyższym punkcie toru?

Zakładamy, że podczas wykonywania tej akrobacji głowa pilota samolotu jest stale zwrócona w stronę środka okręgu, po którym porusza się samolot.

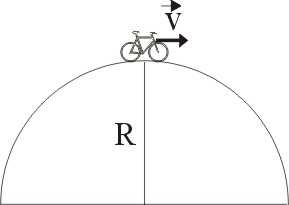
6. Przez wypukły półkolisty mostek o promieniu R = 20 m przejeżdża

rowerzysta. Najwyższy punkt wypukłości mija z szybkością

m

v = 10

.

s

Oblicz siłę nacisku wywieraną na podłoże przez rowerzystę. Łączna

masa jego i roweru wynosi m = 80 kg .

7. Na poziomej tarczy wirującej z prędkością kątową ω położono mały klocek. Współczynnik tarcia klocka o powierzchnię tarczy wynosi µs . Oblicz maksymalną odległość miejsca klocka od osi obrotu, w którym klocek pozostanie jeszcze na tarczy w spoczynku.

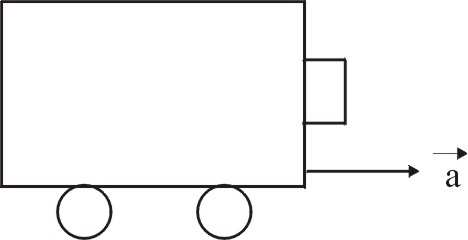
8. Czy możliwe jest, aby ciało w sytuacji przedstawionej na rysunku

spoczywało względem platformy, (nawet, jeśli nie jest do niej

przyklejone)? Odpowiedź uzasadnij.

9. Na kartkę papieru leżącą na stole położono kredę. Oblicz maksymalną wartość

przyspieszenia, z jakim można ciągnąć kartkę, aby kreda na niej pozostała w spoczynku.

Współczynnik tarcia kredy o kartkę wynosi µ = ,

0 2

s

.

3