Egzamin dla Aktuariuszy z 2 czerwca 2008 r.
Matematyka Finansowa
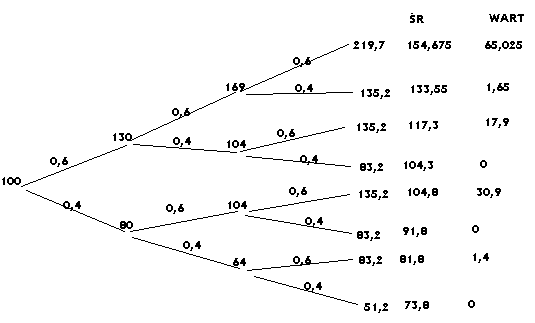
Zadanie 1
WART=max(X-ŚR;0)
CENA = ( 3
2
2
2
2
,
0 6 ⋅ 6 ,
5 025 + ,
0 6
,
0 4 ⋅ ,
1 65 + ,
0 6
,
0 4 ⋅17 9
, + ,
0 6
,
0 4 ⋅ 30 9
, + ,
0 6 ⋅ ,
0 4 ⋅ ,
1 ) 1
4
3
1
,
1 5
æ
100 + 120 + 160 + 150
ö
ZWROT = maxç150 −
0
; ÷ = 17 5
,
è
4
ø
CENA 1
( + i 3
) = ZWROT
1
æ ZWROT ö3
ODP = i = ç
÷ −1 ≈ ,
7
%
46
≈ 6
,
7 %
è CENA ø
Zadanie 2
Xs
= 10000 Ea I ≅ J ( , 0
07
,
0
;
03
)
3 ;
6 0,004
3; I
æ
3 ö
æ 1 ö
æ 1 ö3
ç
÷
1 − ç
÷
0,07 1 − ç
÷
ç
è1+ I ø ÷
0,07
3
0,07
Ea
=
1
x
1
1
(
x)
1
1
1
E
25
25
3; I
ç
÷ = ò
è + ø
= ò
+
− =
3
ò æ
ö
çç −
3 ÷
÷
I
x
,
0 07 − ,
0 03
x 1
( +
ç
÷
x)
x
x 1
(
x)
0,03
0,03
0,03
è
+
ø
ç
÷
è
ø
1
A
B
C
D
( A 1+3 x+3 x 2 + x 3)+ B( x+2 x 2 + x 3)+ C( x+ x 2)+
= +
+
+
=
Dx =
x 1
( + x 3
)
x
1 + x
1
( + x 2
)
1
( + x 3
)
1
( + x 3
) x
x 3 ( A + B) + x 2 3
( A + 2 B + C) + x 3
( A + B + C + D) + A
=
1
( + x 3
) x
ì A = 1
ï
ì A + B = 0
B = −1
ï
ï3
ï A + 2 B + C = 0
3
ï − 2 + C = 0
1
1
1
1
1
í
→ í
→
= −
−
−
3
2
3
3 A + B + C + D = 0
C
ï
= −1
ï
x 1
( + x)
x
1 + x
1
( + x)
1
( + x)
ïî A =1
3
ï −1−1+ D = 0
ïïî D = −1
0,07
,
1 07
Ea
=
1
1
1
1
1
1
25
1
x
t
25
3 I
ò æ
ö
+
+
= + = =
çç
2
3 ÷
÷
ò æ
ö
ç +
+ ÷ =
2
3
1
x
1
(
x)
1
(
x)
t
t
t
0,03
è +
+
+
ø
è
ø
,
1 03
é
1
1 ù ,
1 07
é
1
1
1
1
ù
= 25 ln t − −
=
ê
25 ln 0
,
1 7
ln 0
,
1 3
2 ú
ê
−
−
−
+
+
ú
ë
t
2 t û
0
,
1 7
2
0
,
1 7
0
,
1 3
,
1 03
ë
⋅
2
2 ⋅
2
0
,
1 3 û
Ea
⋅ 0
,
0 04 ⋅10000
3
X =
I
≈ 705
0
,
1 0436 −1
Zadanie 3
S = 53
0
K=50; T=0,75; r=10%; σ = 2 %
0 ; R = K + C − S; R = K − P − S
C
P
Chcemy by: R
R
C = −
c
zyl
i K
P
+ C - S = -K + P + S
100=P+2S-C
100 + C − P
S =
2
C,P wyznaczone dla S = 53
0
−
WIEMY:
rT
C − P = S
0 − Ke
Z tego:
−
100 + 53 − 50 0,075
=
e
S
≈ 53 3
, czyli zmiana wzrost o 0,3
2
Zadanie 4
(i)TAK
E( S
E X
X
X
S
n+ Φ n
=
+ + n + n+ Φ n = n +
1
) (
...
1
1
)
0
(ii)TAK
E( S 2
n 1
E X
...
X
X
2
n 1
n+1 −
− Φ n )= (( 1 + + n + n+1) − − Φ n )=
= E (( X
1 + ... + X
2
2 X
...
X
X
X 2
n 1
n )
+ ( 1 + + n ) n+1 + n+1 − − Φ n )=
= S 2 + 2 S ⋅ 0 +1− n −1 = S 2 − n n
n
n
(iii)TAK
E( E( X
1 Φ +1 Φ
= E X 1 Φ
n
) n) (
n )
Zadanie 5
X
X
X
X
X
300000 =
+
+
+
+
+
1
,
1
1
,
1 ⋅ 0
,
1 8
1
,
1 ⋅ 0
,
1 8 ⋅ 0
,
1 6
1
,
1 ⋅ 0
,
1 8 ⋅ 0
,
1 6 ⋅ 0
,
1 7
1
,
1 ⋅ 0
,
1 8 ⋅ 0
,
1 6 ⋅ 0
,
1 7 ⋅ 0
,
1 4
+
X
+
1
XA
+
1
XA
+ + XAA +
2 1
...
XA
+ ... +
3
XA +
1
,
1 ⋅ ,
1 08 ⋅ ,
1 06 ⋅ ,
1 07 ⋅ ,
1 04 ⋅ ,
1 05
1
,
1
1
,
1 ⋅ ,
1 08
1
,
1
1
4
4
4
4
4
2
4
4
4
4
4
3
A
+
3 1
XA
+ +
4
XA +
4 1
...
XA
+ ... +
5
XA =
1
,
1
1
,
1
é
ù
ê
ú
=
1
1
1
1
X ê
+
+
+ ... +
+ A + AB + A 2 B + A 3 B + A 4 Bú ê 1
,
1
1
,
1 ⋅ 0
,
1 8
1
,
1 ⋅ 0
,
1 8 ⋅ 0
,
1 6
1
,
1 ⋅ 0
,
1 8 ⋅ 0
,
1 6 ⋅ 0
,
1 7 ⋅ 0
,
1 4
ú
ë1
4
4
4
4
4
4
4
4
4
4
4
4
2
4
4
4
4
4
4
4
4
4
4
4
4
3
B
û
2
3
4
1 − 5
= X [ B + AB + A B + A B + A B]
A
= XB
1 − A
300
−
=
A
X
B(000 1
(
≈
5
− A ) ) 24018
1
Zadanie 6
W (A) (B) i (E) rozpatrujemy 1 zł
W C i D rozpatrujemy 1USD
1
(A) kredyt w PLN, dep w EUR DEP =
7
,
0 ⋅ 0
,
1 4 ⋅ ,
3 27 KREDYT=1,09
,
2 2
(DEP – zwrot z depozytu 1 zł w zł; KREDYT>DEP czyli NIE) analogicznie dalej sprawdzamy
(B) kredyt USD, dep PLN DEP=1,06 KREDYT=1/2,2*1,04*2,35 NIE
kredyt PLN, dep USD
DEP=1/2,2*1,02*2,35 KREDYT=1,09
(C) kredyt USD, dep EUR
DEP=0,7*1,04*1/0,72
KREDYT=1,04 NIE
kredyt EUR, dep USD
DEP=1,02
KREDYT=0,7*1,06*1/0,72 NIE
(D) kredyt EUR, dep USD
DEP=1,02
KREDYT=0,7*1,06*1,039 NIE
kredyt USD, dep EUR
DEP=0,7*1,04*1,39 KREDYT=1,04 NIE
(E) kredyt EUR, dep PLN
DEP=1,06
KREDYT=1/2,2*0,7*1,06*1/0,32=1,05 TAK
czyli odpowiedź (E) jest prawidłowa Zadanie 7
Z – zgromadzone środki
= K
Z
⋅
K
3500 ⋅
120
120
,
1 003
,
1 0025
+
3
( 500 +
119
120
30 ,
1
) 003
,
1 0025
+
100
100
+ K
K
3
( 500 + 2 ⋅
118
120
30 ,
1
) 003
,
1 0025
+ ... +
3
( 500 + 119 ⋅ 30 ,
1
) 003 ⋅
120
,
1 0025
+
100
100
K + 3
120
K +
+
3
( 500 + 120 ⋅ 30 ,
1
)
+
3
0025
3
( 500 + 121⋅ 30 ,
1
) 0025119 + ... +
100
100
K +
+
3
K
3
( 500 + 239 ⋅ 30 ,
1
) 0025 =
⋅ 3500 ⋅
120
,
1 0025
s&
&
+
12 ;
0 0,003
100
100
6
4
4
4
4
4
4
4
7
A
4
4
4
4
4
4
4
8
+ K 30 ⋅ 0
,
1 025120 ( 0
,
1 03119 + 2 ⋅ 0
,
1 03118 + ... + 119 ⋅ 0
,
1 0 )
3 +
100
B
K + 3
K + 3
+
3500 &
& s
+
30
⋅
+
⋅
+ +
⋅
12 ;
0 0,0025
(6
4
4
4
4
4
4
4
4
4
7
4
4
4
4
4
4
4
4
4
120
0
,
1 025120
121
0
,
1 025119
...
239
0
,
1 025)
8
100
100
A
= 0
,
1 03118 + 2 ⋅ 0
,
1 03117 + ... + 119
0
,
1 03
æ
ö
s&
&
−119
1
ç
A 1 −
÷ = 0
,
1 03119 + 0
,
1 03118 + ... + 0
,
1 03 −119
11 ;
9 0,003
→ A =
è
0
,
1 03 ø
1
1 − 0,
1 03
B
= 120 ⋅ 0
,
1 025119 + 121⋅ 0
,
1 025118 + ... + 239
0
,
1 025
æ
ö
s&
&
+120 ⋅ ,
1 0025120 − 239
1
Bç1 −
÷ = 120 ⋅ ,10025120 + ,10025119 + ... + , 1 0025 − 239
11 ;
9 0,0025
→ B =
è
,
1 0025 ø
1
1 − ,10025
= K
Z
[3500⋅ ,10025120 s&&
+ 30 ⋅ ,10025120 A + 3500 s&&
+ 30 B
12 ;
0 0,003
12 ;
0 0,
]+
100
0025
+ 0
,
0 3 ⋅ 3500 s&
&
+ 0
,
0 3 ⋅ 30 B
12 ;
0 0,0025
RENTA = 2000 a
= Z
12 ;
0 0,002
120
é
ù
æ 1 ö
ê
1 − ç
÷
ú
ê
è 0
,
1 02 ø
0
,
1 025120 −1
ú
2000
− 0
,
0 3 ⋅ 3500
− 0
,
0 3 ⋅ 30 B 100
ê
ú
0
,
0 2
1
ê
1 −
ú
0
,
1 025
ê
ú
ë
û
K =
, gdzie
0
,
1 03120 −
−
120
1
0
,
1 025120
120
1
3500 ⋅ 0
,
1 025
+ 30 ⋅ 0
,
1 025
A + 3500
+ 30 B
1
1
1 −
1 −
0
,
1 03
0
,
1 025
0
,
1 03119 −1
119
−
0
,
1 025
−1
119
+120 ⋅ 0
,
1 025120 − 239
1
1
1 −
1 −
0
,
1 03
0
,
1 025
A =
B =
1
1
1 −
1 −
0
,
1 03
0
,
1 025
i wychodzi około 7,86
Zadanie 8
P(0,3) – to jest cena jednostkowa czyli jest to dyskonto Aby policzyć w milionach:
120
ODP = E max 4
( X −
−0,08 x −0 1
, 2
400 0
;
x
e
e
= ò 1
)
(4 x −
−0,2
400)
x
e
=
40
100
= [1
,
0 −
−0,2
5
x
xe
−
−0,2
25
x
e
]120 10 5 x
e
100 −
[− −0,2 ]120100 =
=
(1,
0 −
−24
600 e
−
−24
25 e
+
−20
500 e
+
−20
25 e
)−10( −20
5 e
− −24
5 e
)=
2
− 4
2
− 0
−20
= −12 5
, e
+ 5
,
2 e
= 5
,
2 e
(
4
1 − 5 −
e
)
Zadanie 9
σ
r − r = β r − r β =
i
f
i ( M
f )
iM
i
2
σ M
r
X =
1
,
0 + β( ,
0 22 −
)
1
,
0
cov( r , r
X
)
1
,
0 4 =
M
→ cov = 1
,
0 4 ⋅ 6
,
0 ⋅ 5
,
0
3
,
0 6
,
0 25
cov
1
,
0 4 ⋅ 6
,
0 ⋅ 5
,
0
1
,
0 4 ⋅ 6
,
0 ⋅ 5
,
0
β =
=
→ ODP = 1
,
0 + 1
,
0 2
= 1 ,1 %
4
3
,
0 6
3
,
0 6
3
,
0 6
Zadanie 10
A= 0,25*110+0,75*80=87,5 NIE
B = 0,25*160+0,75*110=122,5 nie równa się 130 czyli NIE
C E( S F =
⋅
+
⋅
=
≠
NIE
1
0 )
,
0 25 130
7
,
0 5 100
107 5
,
110
D
E( S F < S
<
NIE
1
0 )
b
o1
07,5
110
0
SPRAWDZAMY E
E( S F ≤ S
≤
1
0 )
b
o1
07,5
110
0
E( S F = S ≤ S OK.
1
1 )
1
1
E( S F =
⋅
+
⋅
⋅
+
⋅
=
≤
OK.
2
0 )
160
,
0 252
110
7
,
0 5
,
0 25 80
7
,
0 52
75 6
, 25
110
E( S F = 130 =
⋅
+
⋅
=
≤
OK.
2
1
) ,025 160 7,
0 5 110
122 5
,
130
E( S F = 100 =
⋅
+
⋅
=
≤
OK.
2
1
) ,025 110 7,
0 5 80
87 5
,
100
czyli (E) odpowiedź prawidłowa