Złożoność obliczeniowa

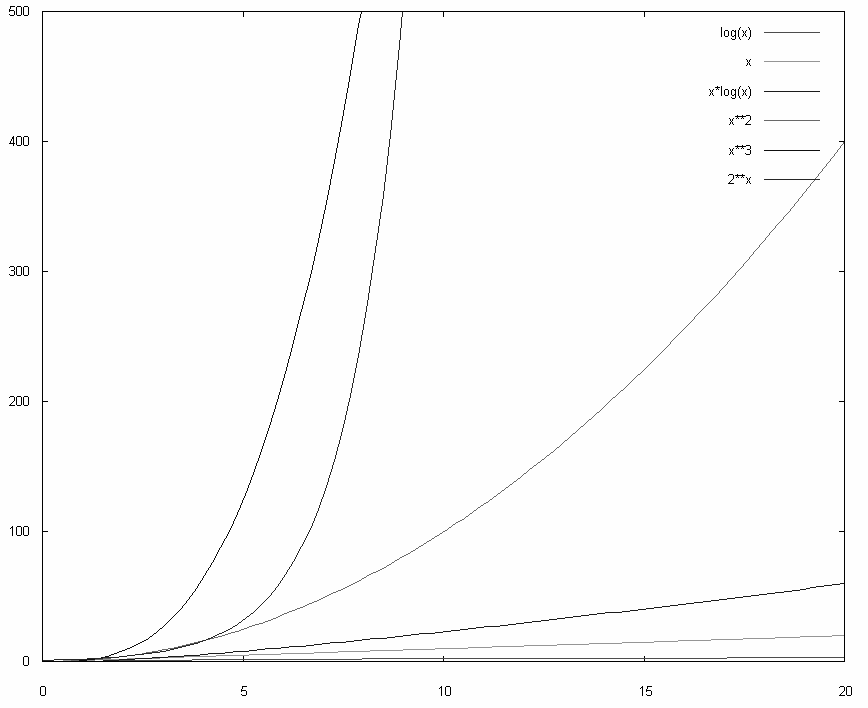
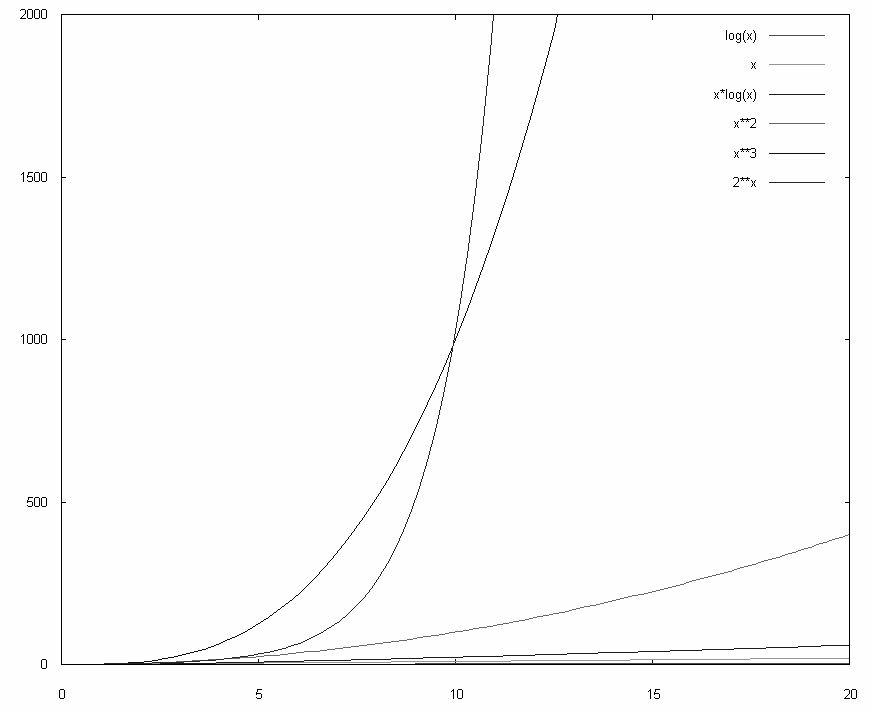
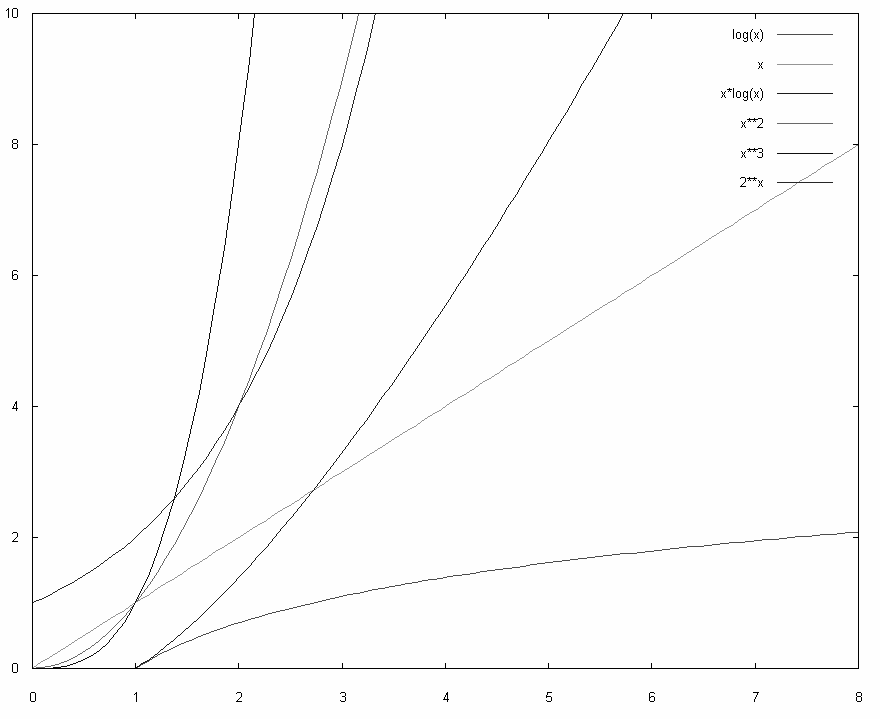
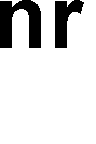Kryteria wyboru algorytmów:

• czas działania

• ilość pamięci niezbędnej do wykonania algorytmu dla określonego zbioru danych wejściowych

• szybkość wzrostu zajętości pamięci i czasu obliczeń przy zmianie liczby danych

Rozmiar problemu:

liczba naturalna będąca miarą wielkości danych wejściowych, np.:

• sortowanie, wyszukiwanie: liczba elementów

• mnożenie macierzy: maksymalny rozmiar macierzy

• analiza grafów: liczba wierzchołków lub krawędzi grafu

Złożoność czasowa algorytmu:

Czas wykonania algorytmu jako funkcja rozmiaru problemu (funkcja kosztu czasowego algorytmu)

T(n), n – rozmiar problemu

Złożoność pamięciowa algorytmu:

Funkcja rozmiaru problemu określająca ilość pamięci potrzebną do realizacji danego algorytmu

S(n)

Złożoność średnia

T ( n)

pr( d ) T ( d )

sr

= ∑

⋅

d∈ Dn

• pr(d) – prawdopodobieństwo wystąpienia zestawu danych d

• Dn – zbiór zestawów danych rozmiaru n

• wada – trzeba znać prawdopodobieństwa

Złożoność pesymistyczna – dla najgorszego przypadku

Tpes(n) = max{ T(d), d – dane rozmiaru n }

Notacja „O” ( order – rząd)

Nieujemna funkcja g(n) jest rzędu co najwyżej funkcji f(n), czyli:

g( n) = O( f( n)) gdy istnieje stała c > 0 taka, że:

g( n) ≤ c⋅ f(n) dla prawie każdego n∈ N

• przy szacowaniu złożoności funkcję g( n) można zastąpić funkcją f( n)

Własność:

g( n) = O( f ( n)) ∧ f ( n) = O( (

h n))

⇓

g( n) = O( (

h n))

Przykład:

12 + 22 + ...

2

+ n = O( 3

n )

Dowód:

12 + 22 + ... + 2

1

1

n =

⋅ n ⋅ ( n + ) ⋅ ( n + ) 1 =

3

2

= 1 ⋅ 3 1 2 1

n +

⋅ n + ⋅ n

3

2

6

1

3

1

2

1

g( n) =

⋅ n + ⋅ n + ⋅ n

3

f ( n) = n

3

2

6

1

1

1

3

2

3

⋅ n + ⋅ n + ⋅ n ≤ c ⋅ n - z definicji 3

2

6

przy c=1:

1

3

1

2

1

3

⋅ n + ⋅ n + ⋅ n ≤ n //⋅6

3

2

6

3

2

3

3

2 ⋅ n + 3 ⋅ n + n ≤ 6 ⋅ n //− 2 ⋅ n

3 ⋅ n2 + n ≤ 4 ⋅ n3 // : n

2

3 ⋅ n + 1 ≤ 4 ⋅ n - prawdziwe dla każdego n∈ N, c.n.d.

np.

• 2

n + n ⋅ log n = O( 2

n )

2

• n ⋅ log n = O( 2

n )

2

szacowanie tym lepsze, im funkcje bliżej siebie

Szacowanie rzędu złożoności obliczeniowej dla wielomianów

m

P ( n)

m

m −1

m −2

= a ⋅ n + a − ⋅ n

+ a − ⋅ n

+ ... + a ⋅ n + a =

m

m 1

m 2

1

0

= O( m

n )

Dowód:

m

m

m

P ( n) ≤ | a | ⋅ n + | a

|

1

⋅ n −1

−

+ ... + | a |

1

⋅ n+ | a |

0

=

m

m

1

1

1

m

= n ⋅ (| a | + | a − |

1

+ ... + | a |

1

+ | a |

)

1

0

≤

m

m

m −

m

n

n

n

m

m

≤ n ⋅ (| a | + | a − |

1

+... + | a |

1

+ | a |)

0

= c ⋅ n

m

m

0

gdzie c = ∑| a |

i

i = m

czyli:

m

m

P ( n) = g( n) ≤ cf ( n) = cn

m

P ( n) = O( m

n ) c.n.d.

Zasady szacowania złożoności czasowych

1. Koszt całkowity (arytmetyczny) algorytmu – liczba wszystkich operacji (działań)

2. Operacja dominująca – liczba takich operacji, potrzebnych do wykonania algorytmu dla dowolnych danych i na dowolnym komputerze jest proporcjonalna do liczby wszystkich wykonywanych operacji.

Złożoność czasowa:

Złożoność czasowa algorytmu A to liczba operacji dominujących potrzebnych do wykonania algorytmu A zależna od rozmiaru problemu.

Przykłady szacowania złożoności czasowych

• Obliczanie wartości wielomianu:

n

n

n −1

n −2

P ( x) = a ⋅ x + a − ⋅ x

+ a − ⋅ x + ... + a ⋅ x + a

n

n 1

n 2

1

0

z definicji:

- rozmiar problemu – n

- potęgowanie zastępujemy mnożeniem

- operacje dominujące – dodawanie i mnożenie ( d i m)

L = n

d

L

z potęgowania

m = ( n −

)

1 + ( n − 2) + ... + 2 + 1 +

+ n

z mnożenia

k

a ⋅ x

k

T ( n) = n + n + ( n − ) 1 + ( n − 2) + ... + 2 + 1 =

n + 1

= n +

⋅ n

2

2

n + 3 n

1 2

3

=

= n + n = O( 2

n )

2

2

2

T ( n) = O( 2

n )

Przykłady szacowania złożoności czasowych

(na podstawie algorytmu)

• Obliczanie wartości wielomianu:

n

n

n −1

n −2

P ( x) = a ⋅ x + a − ⋅ x

+ a − ⋅ x + ... + a ⋅ x + a

n

n 1

n 2

1

0

ze schematu Hornera

P n ( x) = (...(( a ⋅ x + a

)

−

⋅ x + a )

−

⋅ x + ... + a )⋅ x + a

n

n 1

n 2

1

0

- rozmiar problemu – n

- operacje dominujące – dodawanie i mnożenie ( d i m)

na przykład:

1

n = 1

P ( x) = a ⋅ x + a

1

0

2

2

n = 2

P ( x) = a ⋅ x + a ⋅ x + a = ( a ⋅ x + a ) ⋅ x + a

2

1

0

2

1

0

3

n = 3

P ( x) = (( a ⋅ x + a ) ⋅ x + a ) ⋅ x + a

3

2

1

0

- liczba dodawań i mnożeń:

L = n

d

L = n

m

T ( n) = 2 ⋅ n = O( n)

Przykłady szacowania złożoności czasowych

(na podstawie schematu blokowego)

Problem: wyszukiwanie danej x w tablicy n-elementowej

K = p + ( t + d + p + t ) ⋅ n

operacja dominująca: t

T ( n) = 2 ⋅ t ⋅ n

T ( n) = O( n)

Przykłady szacowania złożoności czasowych

(na podstawie schematu blokowego)

Problem: wyszukiwanie danej x w tablicy n-elementowej (wersja z wartownikiem)

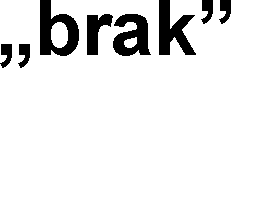
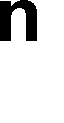
K = p + ( t + d + p) ⋅ ( n + ) 1 + t + t =

=

operacja dominująca: t

( t + d + p) ⋅ n + 2 ⋅ p + 3 ⋅ t + d

T ( n) = t ⋅ n + 3 ⋅ t

T ( n) = O( n)

Przykłady szacowania złożoności czasowych

(na podstawie pseudokodu)

Problem: wyznaczanie iloczynu il = n ⋅ m z definicji

begin

il := 0;

N := n;

while N > 0 do

begin

il := il + m;

N := N – 1;

end

end

K = 2 p + ( t + 2 p + d

2 ) ⋅ n + t

• operacja dominująca: dodawanie d, wtedy złożoność „dokładna”:

T ( n) = 2 d n

• złożoność rzędu:

T ( n) = O( n)

Przykłady szacowania złożoności czasowych

(na podstawie pseudokodu)

Problem: wyznaczanie iloczynu il = m ⋅ n wykorzystując bitową postać mnożnika

begin

il := 0;

N := n;

S := m;

while N <> 0 do

begin

if Odd( N) then il := il + S;

N := N div 2;

S := 2 * S

end

end

r

r −

r −

gdzie

1

2

1

0

N = 2 + 2

+ 2 + ... + 2 + 2

oraz r = log N

2



K = 3 p + ( t + t + d + 2 p + m ) ⋅

n + t + p + d ⋅ γ n

n

2

2

log2 

(

)

( )

gdzie γ ( n) - liczba jedynek w rozwinięciu binarnym liczby n

• operacja dominująca: dodawanie d

T ( n) = d ⋅ γ ( n)

• przypadek pesymistyczny: n złożone z samych jedynek:

γ ( n) = log n

2



• złożoność „dokładna”:

T ( n) = d ⋅ log n

2



• złożoność rzędu:

T ( n) = O(log n) 2

n

1

2

3

4

5

6

7

8

9

10

20

50

100

log2n

0

1 1,58

2 2,32 2,58

2,8

3

3,17

3,32

4,32

5,64

6,64

n

1

2

3

4

5

6

7

8

9

10

20

50

100

nlog2n

0

2 4,57

8 11,61 15,51 19,65

24 28,53

33,22

86,44 282,19 664,38

n2

1

4

9

16

35

36

49

64

81

100

400

2500

10000

n3

1

8

27

64

125

216

343 512

729

1000

8000 125000 1000000

2n

2

4

8

16

32

64

128 256

512

1024 1048576

1015

1030

n!

1

2

6

24

120

720 5040 4032 362880 3628800

2⋅1018 3⋅1064

10157

Maksymalny rozmiar problemu w czasie:

Złożoność

1s

1min

1h

n

1000

6⋅104

3,6⋅106

nlog2n

140

4893

2⋅105

n2

31

244

1897

n3

10

39

153

2n

9

15

21

1op=0,001s

Problem rozmiaru 10000

Złożoność

[op]

czas

n

10000

10s

nlog2n

13⋅104

130s

n2

108

28h

n3

1012

~32 lata

2n

210000

???

1op=0,001s

Max rozmiar problemu

Złożoność

1x

przsp. 10x

n

s1

10⋅s1

nlog2n

s2

10⋅s2

dla dużych n

n2

s3

3,16⋅s3

n3

s4

2,15⋅s4

2n

s5

s5+3,3

1op=0,001s