Kamil Pieńkowski gr.24
TEMAT : KONDENSACJA KAPILARNA - PORY TYPU BUTELKOWATEGO
Kondensacja kapilarna - zjawisko wcześniejszej kondensacji pary w kapilarach, przed osiągnięciem ciśnienia pary nasyconej po nad płaską powierzchnią.
Adsorpcyjne warstwy adsorbatu pokrywające ściany kapilar porowatego adsorbentu mają wygiętą powierzchnię (wklęsłą) i ciśnienie pary nasyconej nad nimi jest niższe niż nad powierzchnią płaską, dlatego kondensacja pary na tych zakrzywionych warstwach zachodzi przy mniejszym ciśnieniu niż wynosi wartość po adsorbowanej substancji. Termodynamiczne rozważania pozwalają wyprowadzić zależność pomiędzy prężnością pary nasyconej nad powierzchnią zakrzywioną (p) i prężnością pary nasyconej nad płaską powierzchnią cieczy (po). Zależność tą wyprowadził W.Thomson (Kelvin):
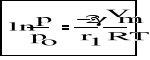
(1)
Gdzie : r1 - promień krzywizny powierzchni cieczy
γ - napięcie powierzchniowe cieczy
Vm - objętość molowa cieczy
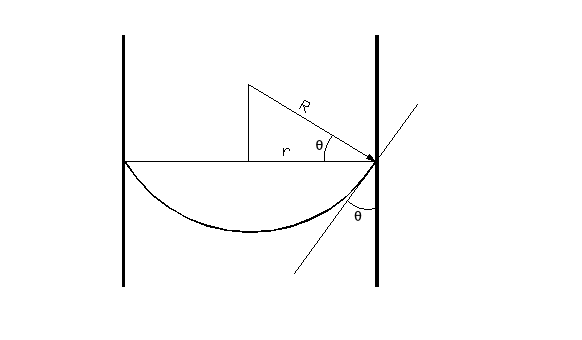
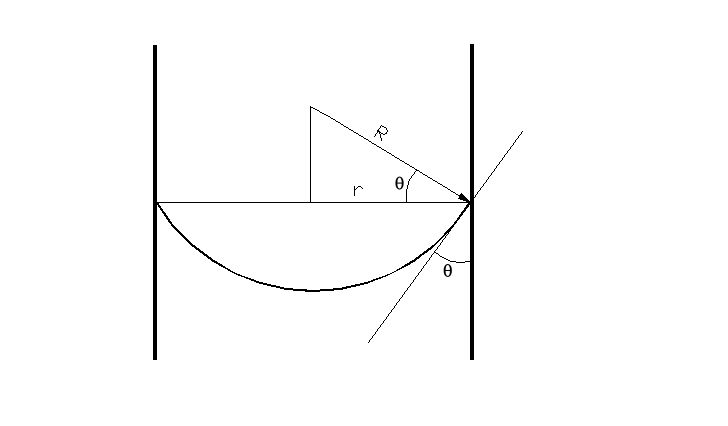
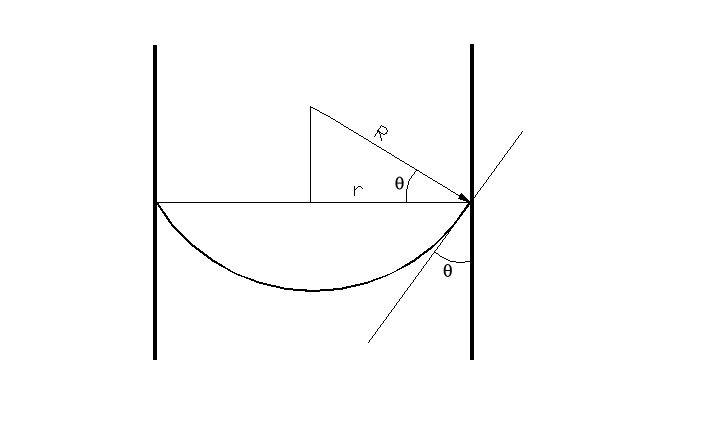
W przypadku cieczy znajdującej się w cylindrycznej kapilarze (i w szyjce butelki) istnieje związek pomiędzy promieniem tej kapilary r, a promieniem krzywizny menisku:
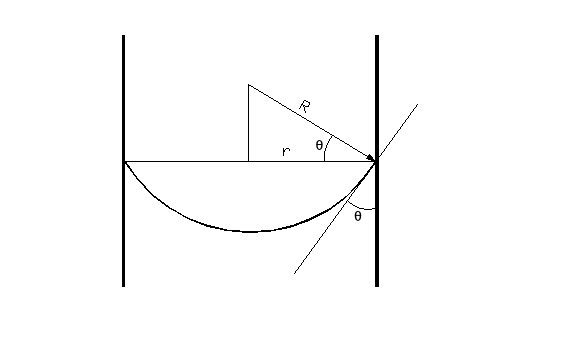
r = r1cosθ, gdzie θ - kąt zwilżania (2)
Łącząc równania (1) i (2) otrzymamy zależność prężności pary nasyconej od promienia kapilary :
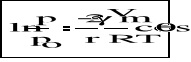
(3)
Dla cieczy silnie zwilżającej ściany kapilary kąt θ równa się zero i wówczas cosθ = 1, czyli promień kapilary jest praktycznie równy promieniowi krzywizny menisku cieczy.
Jeżeli menisk cieczy ma kształt cylindryczny, to zamiast równania (1) napiszemy :
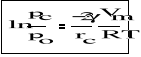
(4)
gdzie : pc - prężność pary nad meniskiem cylindrycznym
rc - promień krzywizny cylindrycznego menisku cieczy
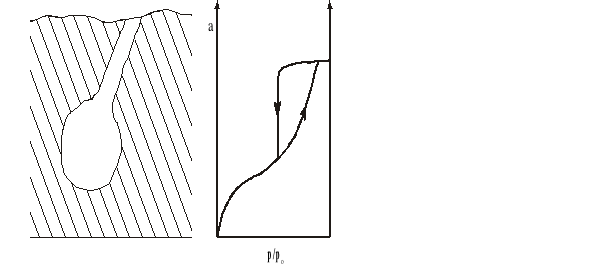
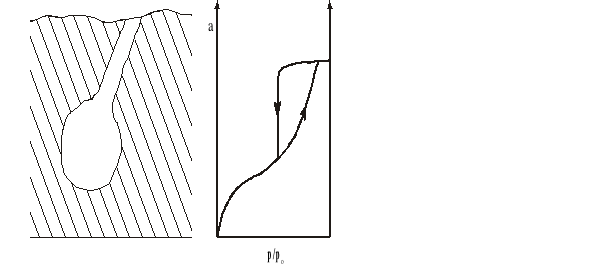
Równanie (4) nazywamy równaniem Cohana i wynika z niego, że ciśnienie pary nasyconej nad powierzchnią cieczy o kształcie cylindrycznym (wklęsłym) obniża się w mniejszym stopniu niż nad wklęsłą powierzchnią cieczy będącej wycinkiem kuli, czyli pc > pk. Związane jest z tym zjawisko histerezy kondensacji kapilarnej. Histereza kondensacji kapilarnej występuje bardzo często i jest ściśle związana z kształtem kapilar adsorbentu. Zjawisko histerezy polega na tym, że zazwyczaj w zakresie wysokich ciśnień względnych część izotermy odpowiadająca pomiarom wykonywanym przy stopniowym wzroście ciśnienia (krzywa adsorpcji) ma inny przebieg niż część izotermy odpowiadającej obniżaniu ciśnienia (krzywa desorpcji).
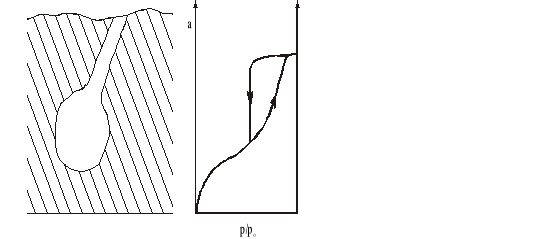
T = const
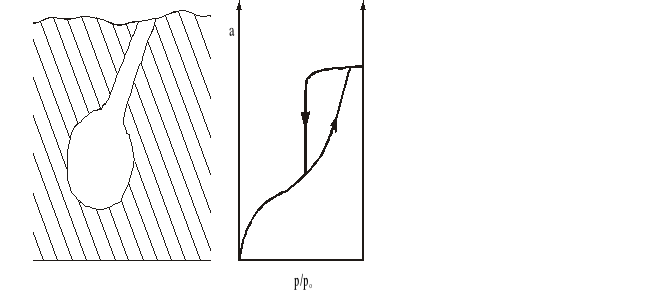
Podczas kondensacji w kapilarach o kształcie butelkowatym szyjka o małym promieniu zapełnia się skondensowaną cieczą już przy stosunkowo niskim ciśnieniu p', podczas gdy szeroka wewnętrzna część kapilary zapełnia się przy ciśnieniu znacznie wyższym (wartość p/po musi odpowiadać promieniowi szerszej części kapilary). W czasie desorpcji wnętrze „butelki” może się opróżnić dopiero wtedy, gdy zostanie opróżniona szyjka, tj. gdy ciśnienie spadnie poniżej p'.
Według Cohena w czasie adsorpcji następuje stopniowe wypełnianie kapilar, tak jak to przedstawia teoria adsorpcji wielowarstwowej, a równanie Kelvina stosuje się tylko do krzywej desorpcji.
Po desorpcji ściana kapilary pozostaje jeszcze pokryta jedno- lub dwucząsteczkową warstwą i jej promień ulega zmniejszeniu:
rk = r - ta (5)
gdzie: r - promień kapilary
rk - średni promień swobodnej przestrzeni adsorpcyjnej między zaadsorbowanymi warstewkami
ta - grubość warstewki zaadsorbowanej
W szyjkach porów butelkowatych menisk powstanie, gdy grubość błonki zaadsorbowanej stanie się porównywalna z promieniem poru, tak więc pory o promieniu mniejszym od przybliżonej wartości średnicy cząsteczki nie mogłyby wywoływać zjawiska histerezy (jako krytyczną wartość promienia przyjęto podwójną średnicę cząsteczki).
Literatura:
„Adsorpcja” J. Ościk
„Chemia Fizyczna” Praca zbiorowa
„Chemia fizyczna powierzchni” A.W. Adamson
„Podstawy techniki adsorpcyjnej” N.W. Kielcew
TEMAT : KONDENSACJA KAPILARNA - PORY TYPU BUTELKOWATEGO
Kondensacja kapilarna - zjawisko wcześniejszej kondensacji pary w kapilarach, przed osiągnięciem ciśnienia pary nasyconej po nad płaską powierzchnią.
Zależność pomiędzy prężnością pary nasyconej nad powierzchnią zakrzywioną (p) i prężnością pary nasyconej nad płaską powierzchnią cieczy (po):
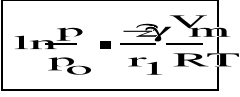
Gdzie : r1 - promień krzywizny powierzchni cieczy
γ - napięcie powierzchniowe cieczy
Vm - objętość molowa cieczy
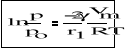
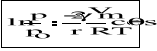
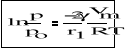
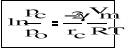
Wyszukiwarka
Podobne podstrony:
MENOPAUZA DIETA Aleksandra Łukaszek gr 6b
HIPERBARIA Edyta Kawecka Aleksandra Łukaszek gr 6 b
HIPOTERMIA Aleksandra Łukaszek Edyta Kawecka gr 6b
zanieczyszczenie zywnosci Aleksandra Łukaszek Edyta Kawecka gr 6b
Łukasz Mąka GR 3
dobor baterii kondensatorów niskiego napiecia lukasz mateja marcin puszko
Aksjologia (gr
KONDENSATORY
Budżet i podatki gr A2
SEM odcinek szyjny kregoslupa gr 13 pdg 1
charakterystyka II gr kationów
13 ZACHOWANIA ZDROWOTNE gr wtorek 17;00
termoregulacja gr II
prezentacja edukacja muzyczna gr 3
MIK Kondensacja
Diety gr 2
więcej podobnych podstron