TEST ZGODNOŚCI CHI-KWADRAT

Test zgodności chi-kwadrat służy do weryfikowania hipotezy, że obserwowana cecha X charakteryzuje się w populacji określonym rodzajem rozkładu.

Hipotezę zerową formułujemy słownie w zależności od tego, jakim rozkładem charakteryzuje się badana cecha. Przykłady hipotezy zerowej zostały zaprezentowane poniżej:

1. H₀: cecha X ma rozkład określony dystrybuantą F(x) = F₀(x),

2. H₀: cecha X ma rozkład N(m,σ),

3. H₀: cecha X ma rozkład Poissona.

Sprawdzianem hipotezy zerowej jest statystyka wyrażona w następujący sposób:

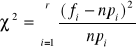
Statystyka testu ma rozkład χ² o ν = k - r - 1 stopniach swobody, gdzie r to liczba szacowanych parametrów, od których zależy rozkład cechy w populacji, natomiast k to liczba przedziałów klasowych lub wariantów cechy X;

pi oznacza prawdopodobieństwo tego, że cecha X przyjmuje wartość należącą do i-tego przedziału klasowego, n⋅pi oznacza liczbę jednostek, które powinny znaleźć się w i-tym przedziale (przy założeniu, że cecha ma rozkład zgodny z hipotetycznym).

Jeżeli
, to nie ma podstaw do odrzucenia hipotezy zerowej, w przeciwnym przypadku istnieją podstawy do odrzucenia hipotezy zerowej.

Przykład

Na podstawie danych zawartych w poniższej tablicy należy odpowiedzieć na pytanie czy na poziomie istotności 0,05 można sądzić, że rozkład dziennej liczby dostaw dla pewnego przedsiębiorstwa Z w ciągu 90 dni jest rozkładem Poissona?

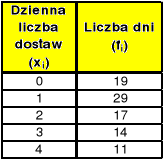
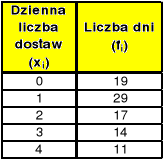
Tab. Dzienna liczba dostaw dla przedsiębiorstwa Z

Przez X oznaczamy dzienną liczbę dostaw do przedsiębiorstwa Z. Hipotezę zerową i alternatywną zapisujemy w następującej postaci:

H₀: X ma rozkład Poissona,

H₁: X nie ma rozkładu Poissona.

W rozkładzie Poissona wartości prawdopodobieństw są funkcją parametru m. Wartość parametru m jest nieznana, w związku z czym najpierw należy parametr ten oszacować na podstawie próby. Ponieważ w rozkładzie Poissona parametr m = E(X), można zatem do oszacowania tego parametru przyjąć estymator wartości przeciętnej. Otrzymujemy wartość średnią równą 1,656 (obliczenia znajdują się w arkuszu kalkulacyjnym MS Excel, do którego link znajduje się na końcu strony), stąd zaokrąglając przyjmujemy m = 1,7. Prawdopodobieństwa p_i znajdujemy w tablicach rozkładu Poissona dla m = 1,7 tak, że p_i = P(X = x_i). Ostatnia wartość p_i wynosi 0,092, jako różnica między jednością a sumą p_i poprzednich.

Dzienna liczba dostaw (xi)	Liczba dni (fi)	xifi
0	19	0
1	29	29
2	17	34
3	14	42
4	11	44
Suma	90	149
wartość przeciętna	1.656

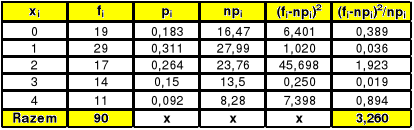
W celu wyznaczenia statystyki testu χ² należy dokonać pewnych obliczeń, które zawiera poniższa tablica:

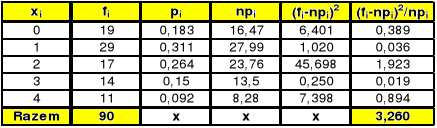
Tab. Obliczenia pomocnicze

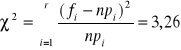
Wartość statystyki testu χ_0,05² odczytana z tablic dla ν = 5 - 1 - 1 = 3 stopniach swobody wynosi 7,815.

Ponieważ χ² < χ²_α, to nie ma podstaw do odrzucenia hipotezy zerowej, że rozkład liczby dostaw jest rozkładem Poissona.