1. Cel ćwiczenia

Celem ćwiczenia jest :

a) zaznajomienie się z pomiarami rezystancji za pomocą technicznego mostka Wheatstone'a,

b) pomiar zależności rezystancji metalu i półprzewodnika w zakresie od temperatury pokojowej do około 450°K,

c) wyznaczenie współczynnika temperaturowego rezystancji oraz szerokości pasma wzbronionego półprzewodnika.

2. WSTĘP TEORETYCZNY

2.1 Metale

W metalach swobodnymi nośnikami ładunku są elektrony nie zapełnionego pasma przewodnictwa. Ich koncentracja nie zależy od temperatury i jest rzędu koncentracji atomów.

Konduktywność metali natomiast ściśle zależy od procesów rozproszeniowych wpływających na prędkość uporządkowanego ruchu nośników. Jednym z mechanizmów rozpraszania są drgania cieplne atomów rozmieszczonych w węzłach sieci krystalicznej. Rozpraszanie to polega na zderzeniach elektronów z fononami, czyli odpowiednikami fotonów w kwantowej teorii drgań mechanicznych. Zatem wraz ze wzrostem temperatury maleje prędkość elektronów w kierunku pola elektrycznego, zatem rezystancja metalu rośnie.

Dla mało zanieczyszczonych jednoskładnikowych metali prawdziwa jest z dobrym przybliżeniem następująca zależność:

gdzie
- rezystancja w temperaturze 0°C,

- rezystancja w temperaturze t°C

- współczynnik temperaturowy rezystancji w zakresie od 0 do t°C

oraz

W praktyce jednak wygodniej jest za rezystancję odniesienia przyjąć rezystancję w temperaturze pokojowej. Stąd współczynnik
ma postać:

2.2 Półprzewodniki

W ćwiczeniu badamy właściwości półprzewodników w zakresie temperatur przewodnictwa samoistnego.

Wystąpienie przewodnictwa elektrycznego w półprzewodnikach samoistnych możliwe jest po dostarczeniu odpowiedniej porcji energii.

Powinna być ona dostatecznie duża, by zdołać przenieść elektron z zapełnionego pasma walencyjnego do najbliższego pasma przewodnictwa oddalonego o przerwę energetyczną Eg.

W miejscu zwolnionym przez elektron w paśmie walencyjnym pojawia się tzw. „dziura”.

Zatem w odpowiednio wysokiej temperaturze w przewodniku samoistnym pojawiają się dwa częściowo zapełnione pasma: pasmo przewodnictwa z pewną liczbą elektronów swobodnych i pasmo walencyjne z identyczną liczbą zwolnionych miejsc - dziur.. Tylko w tej sytuacji możliwe jest przewodzenie prądu elektrycznego.

Na całkowitą przewodność elektryczną półprzewodnika mają wpływ dwie wielkości: przewodnictwo domieszkowe w zakresie niskich temperatur i przewodnictwo samoistne w zakresie temperatur wysokich.

Przy pewnej temperaturze kończy się wpływ atomów domieszek na zjawisko przewodzenia prądu. Obserwujemy wówczas, że zależność

opisująca wzrost koncentracji nośników pod wpływem temperatury zachowuje się liniowo.

Wykorzystując ten fakt można dokonać następujących zapisów:

opisuje kąt nachylenia prostej

stąd

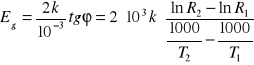
, gdzie
,
oraz
,
oznaczają współrzędne punktów początku i końca prostoliniowego odcinka wykresu
.

Z ostatniej zatem zależności wyznaczyć możemy szerokość pasma wzbronionego półprzewodnika.

3. UKŁAD POMIAROWY

K - komora pomiarowa

G - grzejnik

Rm - rezystor metalowy

Rs - rezystor półprzewodnikowy

T - termometr

Tr - transformator ochronny

At - autotransformator

5. OPRACOWANIE WYNIKÓW

Przykładowe obliczenia błędów pomiarowych w temperaturze początkowej i końcowej:

dla t=295.5K R=0.039 R=9.540 t=0.5

ln(R-R)=ln(9.540-0.039)=2.251

ln(R+R)=ln(9.540+0.039)=2.260

1000/(t-t)=1000/(295.5-0.5)=3.3898

1000/(t+t)=1000/(295.5+0.5)=3.3784

dla t=362.0K R=0.004 R=0,757 t=0.5

ln(R-R)=ln(0.757-0.004)= -0.284

ln(R+R)=ln(0.757+0.004)= -0.273

1000/(t-t)=1000/(362.0-0.5)=2.7662

1000/(t+t)=1000/(362.0+0.5)=2.7586

Obliczam temperaturowy współczynnik rezystancji a z wzoru wymienionego we wstępie teoretycznym.

Za temperaturę t przyjmuję 362K.

Obliczam szerokość pasma wzbronionego w półprzewodniku:

k = 1,38054*10-23 J/K- stała Boltzmanna

T2=295.5K, T1=362.0K, R2=9,54 kW, R1=0.757 kW

lnR2=2.255

lnR1= -0.278

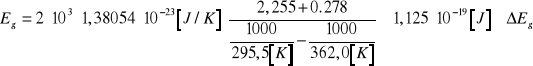
Wiemy, że 1eV=1,6*10-19 [J]

Zatem Eg
0,703 [eV]±DEg

6. RACHUNEK BŁĘDÓW

Całkowity błąd wyznaczania współczynnika rezystancji wynika z błędu multimetru i błędu odczytu z termometru. Otrzymamy go korzystając z metody różniczki zupełnej.

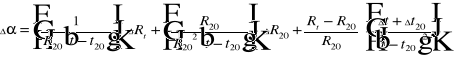
t, t20 ,błędy odczytu temperatury (293K i 362K) wynikające z błędu odczytu z termometru.

t, t20 =0,5°K

,

- błędy bezwzględne pomiaru rezystancji w temperaturze 293K i 362K

=0,1350 kW,

=0,1073 kW,

=0,0005

=0,0004

Po wstawieniu wszystkich danych do wzoru na błąd bezwzględny uzyskujemy wynik:

= 0,000176
0,0002

Ostatecznie =0.00370.0002

Błąd względny wyznaczenia współczynnika
wynosi:

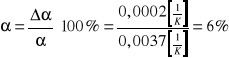
Błąd wyznaczania wartości przerwy energetycznej półprzewodnika wyznaczamy również metodą różniczki zupełnej:

,

T1=362 K DT2 =0,5 K,

T2=295,5 K, DT2=0,5 K,

R1=0.757 kW, DR1= 0.004,

R2=9.540kW, DR2= 0,039,

Po podstawieniu tych wartości do powyższego wzoru otrzymujemy:

DEg
0,004[eV],

Ostatecznie Eg=0,7030,004 [eV]

7.WNIOSKI I DYSKUSJA BŁĘDÓW

Pomiar dzięki dość dużej dokładności użytych przyrządów (cyfrowych multimetrów) może dość dobrze odtwarzać rzeczywisty obraz zmian rezystancji pod wpływem temperatury. Niemniej wartoby w nim polepszyć metodę pomiaru temperatury. W tym celu należałoby zastąpić zwykły termometr termoparą. Mielibyśmy wtedy przy odpowiednio dokładnej termoparze, błąd pomiaru temperatury przynajmniej o rząd mniejszy od otrzymanego. Ważny wpływ na pomiar ma jego prędkość, przy ochładzaniu układu temperatura spadała tak szybko, że występowały problemy z odczytem rezystancji. Pomiaru należałoby dokonywać wolniej, ale na to nie pozwalał brak czasu, a najlepszym rozwiązaniem byłby automatyczny zapis wyników ( multimetry i termopara sprzęgnięte z komputerem ).

Eksperyment potwierdza w granicach błędu liniowy związek między temperaturą metalu, a jego rezystancją. Dowiedzieliśmy się też, a nawet udowodniliśmy, że wraz ze wzrostem temperatury półprzewodnika rośnie wykładniczo liczba elektronów w paśmie przewodnictwa, a tym samym maleje jego rezystancja. Otrzymany wynik temperaturowego współczynnika rezystancji dla mierzonego przez nas przewodnika jest zbliżony dla wartości zawartej w tablicach dla platyny ( 0.0039 [1/K] ). Dodatkowo stwierdzić należy, że przewodniki, w odróżnieniu od półprzewodników bardzo sztywno reagują na zmiany temperatury. Stąd w technice pomiarów temperatury wykorzystuje się głównie te ostatnie. Ich typowym przedstawicielem jest mierzony przez nas NTC 210. To termistor o ujemnym współczynniku temperaturowym w małej obudowie o nominalnej rezystancji równej 10 k. Stosuje się go w prostych termometrach elektronicznych ( ich rozdzielczość to około 0.05C ), gdzie pracuje on jako czujnik temperatury, połączony ze wzmacniaczem operacyjnym np. A 723.

---