Opole, dn. 10 marca 2004

Laboratorium Algorytmów i Struktur Danych

Temat:

Analiza algorytmów wyszukujących

Autor: Dawid Najgiebauer

Informatyka, sem. II, grupa lab. 11

Prowadzący: dr inż. Jan Sadecki

1. Temat

Przeanalizować, zbadać i porównać algorytmy wyszukiwania: sekwencyjnego (liniowego) i binarnego.

2. Analiza, projektowanie

Celem badania jest sprawdzenie praktycznego zastosowania i efektywności algorytmów wyszukujących dane: algorytmu wyszukiwania liniowego oraz algorytmu wyszukiwania binarnego.

Z racji, że podstawą metodyczną działania drugiego z algorytmów jest założenie, że przeszukiwany ciąg jest uporządkowany, wszystkie badania obu algorytmów będą przeprowadzane właśnie na takim ciągu liczb.

Tablica będzie zawierała liczby typu long int, o pewnym losowym rozrzucie (kolejna liczba będzie większa od poprzedniej o wartość losową z zakresu 0 do - z założenia - 100).

Druga tablica będzie zawierała spis licz, które będą wyszukiwane. Wielkość tej tablicy będzie odpowiadać ilości badań w ramach badania dla jednego rozmiaru tablicy liczb. Wartości zawarte w tablicy tej będą losowe i mieścić się w przedziale od 0 do maksimum wyznaczanym przez wartość ostatniej z liczb w tablicy, w której będzie przeprowadzane wyszukiwanie.

1. Algorytm wyszukiwania sekwencyjnego (liniowego)

Algorytm ten, bardzo prosty w założeniach; sprowadza się do porównywania kolejnych wartości z ciągu z szukaną wartością, aż do momentu odnalezienia pierwszej z nich.

Istnieją dwie wersje tego algorytmu: tradycyjny oraz z tzw. „wartownikiem”. Pierwszy z nich sprawdza zarówno, czy aktualnie analizowana liczba jest tą szukaną oraz sprawdza, czy został osiągnięty koniec ciągu. Druga z wersji algorytmu zakłada, że dana wartość w ciągu musi wystąpić. Stąd na końcu wyszukiwanego ciągu wstawia się tzw. „wartownika” - wartość identyczną z poszukiwaną. W ten sposób założenie algorytmu zostanie spełnione, a wyeliminowana zostaje konieczność sprawdzania, czy został osiągnięty kres ciągu.

Łatwo policzyć, że złożoność takiego algorytmu powinna być wprost proporcjonalna do wielkości tablicy, wśród której elementów przeprowadzane jest wyszukiwanie i można określić wzorem Z=N;

2. Algorytm wyszukiwania binarnego (bisekcja)

Algorytm ten to wyszukiwanie informacji w uporządkowanym ciągu elementów, polegający na połowieniu ciągu i odnoszeniu kolejnego kroku do tej połowy, w której można oczekiwać występowania poszukiwanego elementu. Intuicyjną metodę wyszukiwania (nazywaną interpolacyjną), zbliżoną do ścisłego wyszukiwania biernego, stosuje każdy przy korzystaniu np. ze słownika, otwierając go zrazu w dowolnym miejscu i zaglądając na lewo lub na prawo w zależności od napotkanego wyrazu.

Schemat tego algorytmu przedstawiony jest poniżej:

Prześledźmy zasadę działania tego algorytmu na przykładzie:

Dajmy ciąg 20 liczb uporządkowanych: 3, 5, 7, 9, 12, 15, 17, 19, 23, 37, 53, 70, 80, 91, 115, 116, 120, 131, 139, 140. W ciągu tym będziemy wyszukiwać wartość 120.

Tabela 1. Przykład działania algorytmu wyszukiwania binarnego.

3

5

7

9

12

15

17

19

23

37

53

70

80

91

115

116

120

131

139

140

L

S

P

3

5

7

9

12

15

17

19

23

37

53

70

80

91

115

116

120

131

139

140

L

S

P

3

5

7

9

12

15

17

19

23

37

53

70

80

91

115

116

120

131

139

140

L

S

P

3

5

7

9

12

15

17

19

23

37

53

70

80

91

115

116

120

131

139

140

L

S

P

Nr	Ciąg do analizowania	Zmienne
1.		L=0; P=19; S=9 37<120 - TAK
2.		L=10; P=19; S=14 115<120 - TAK
3.		L=15; P=19; S=17 131<120 - NIE
4.		L=15; P=17; S=16 120=120 - TAK -wynik: 16

Jak widać na powyższym przykładzie do odnalezienia szukanej liczby wystarczyły zaledwie 3 przebiegi. Porównując to do algorytmu wyszukiwania sekwencyjnego, gdzie w powyższym przypadku potrzeba by do odnalezienia szukanej liczby aż 17 przebiegów, wyszukiwanie binarne jest o wiele szybsze i dużo mniej złożone. Dodatkowo złożoność tego algorytmu jest logarytmicznie rosnąca wraz ze wzrostem liczby elementów do przeszukania, a więc im więcej elementów, tym bardziej zaznacza się większa szybkość jego działania względem wyszukiwania liniowego.

Łatwo zauważyć, że ilość potrzebnych operacji układa się w charakterystyczny ciąg: (((N/2)/2)/...)/2), a więc da się wyrazić wzorem:

3. Implementacje i wykonanie badań algorytmów

1. Założenia

Badania zostaną wykonane dla ciągów o różnej długości. Począwszy od ciągu o długości 50 000 elementów a na ciągu zawierającym 1 milion elementów skończywszy, zwiększając za każdym razem długość ciągu o 50 000. Ze względu na to, iż oba algorytmy są bardzo szybkie, a także chcąc uzyskać wyniki uśrednione czasu działania każdego z algorytmów, zostanie zmierzony czas łączny dla 5 000 wykonań w przypadku algorytmu wyszukiwania liniowego i 1 000 000 wykonań dla algorytmu wyszukiwania binarnego. Aby uzyskać jak najbardziej obiektywne wyniki za każdym razem będzie wybierana inna liczba, która ma zostać znaleziona. Będzie to liczba pochodząca z tablicy o ilości 5 000 elementów z losowymi liczbami z zakresu zero do maksimum, czyli wartości ostatniego elementu z tablicy, w której będzie przeprowadzane wyszukiwanie. Dla każdego z algorytmów będzie obowiązywał ten sam zestaw liczb, wśród których będzie przeprowadzane wyszukiwanie oraz ten sam zestaw liczb, które mają zostać odnalezione. Następnie zmierzony czas zostanie podzielony przez liczbę wykonań.

2. Implementacja algorytmu wyszukiwania liniowego bez „wartownika” i z „wartownikiem”

long SzukajSekwencyjnie(long *tab, long n, long x)

{

for(long i=0;i<n;i++)

if (tab[i]==x) break;

return i;

}

long SzukajSekwencyjnieWart(long *tab, long n, long x)

{

long i=0;

tab[n]=x; //wartownik

while (tab[i]!=x) i++;

return i;

}

3. Implementacja algorytmu wyszukiwania binarnego

long SzukajBinarnie(long *tab, long n, long x)

{

int l=0; //ogranicznik z lewej

int p=n; //ogranicznik z prawej

int s; //środek badanego zakresu

while (l<p)

{

s=(l+p)/2;

if (tab[s]==x) return s;

else

if (tab[s]<x)

l=s+1;

else

p=s;

}

if (x==tab[l]) return l; else return n;

}

4. Wyniki badania

Czas wykonywania algorytmów dla poszczególnych danych przedstawiono na wykresie poniżej. Należy zwrócić uwagę, że wykres dla algorytmu wyszukiwania binarnego odnosi się do prawej osi i jest wyrażony w µs.

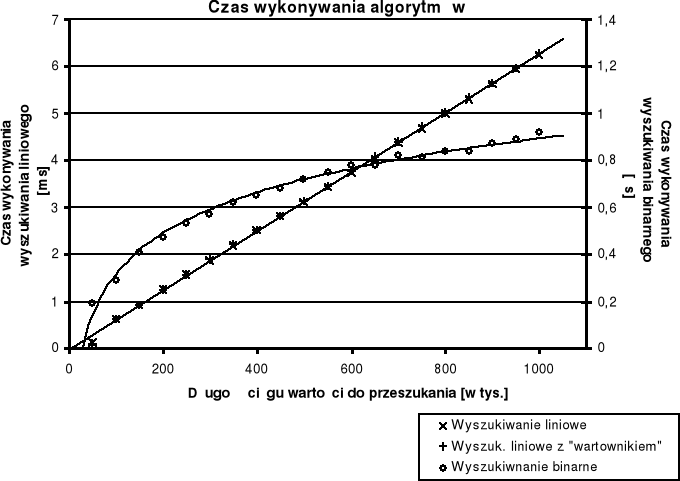
Rysunek 1. Wykres zależności czasu wykonywania algorytmów od wielkości przeszukiwanej tablicy.

5. Uwagi i wnioski z testowania i uruchamiania

1. Czas wyszukiwania wartości algorytmem wyszukiwania sekwencyjnego jest wprost proporcjonalny do wielkości ciągu, jaki należy przeszukać.

2. Praktycznie nie występują różnice między wyszukiwaniem sekwencyjnym z i bez „wartownika”. Prawdopodobnie spowodowane jest to dużą optymalizacją kodu przez kompilator szczególnie pod względem porównywania statycznych zmiennych; kluczową rolą jest czas odwoływania się do zmiennej dynamicznej o bardzo wysokim adresie (co z resztą widać po czasach wykonywania się algorytmów dla 50 000 danych - są dużo krótsze od wyznaczonego trendu). Wyniki obu wariantów algorytmów wspólnie oscylują wokół linii trendu.

3. Charakterystyka zależności czasu wykonywania od długości tablicy dla wyszukiwania binarnego zgodnie z założeniami tworzy trend logarytmiczny.

4. Duże odbieganie punktów od linii trendu może być spowodowane doborem zbyt małej ilości przeprowadzanych badań - wyniki obarczone są większym błędem.

5. Przewaga w czasie wykonywania algorytmu wyszukiwania binarnego nad wyszukiwaniem liniowym rośnie bardzo szybko wraz ze wzrostem długości ciągu, w którym przeprowadzane jest wyszukiwanie. Jednocześnie zawsze wyszukiwanie binarne jest o rząd wielkości szybsze od sekwencyjnego.

6. Przyczyną „minięcia” się linii trendów z punktem (0,0) jest najprawdopodobniej fakt, iż część czasu procesora była pochłonięta przez wywoływanie funkcji (które było wykonywane wielokrotnie - dla bisekcji nawet milion razy).

W przypadku algorytmu binarnego, ze względu na potrzebę wykonania większej ilości wyszukiwań, wyszukiwanych będzie także ten sam zestaw 5 000 liczb, ale każda z liczb będzie wyszukiwana 200 razy (nie następującej po sobie).

6 Dawid Najgiebauer

Wyniki badania 7

Temat 3

I<N

N, tab[], X

I=0

tab[N]=X

X!=tab[I]

I++

T

N

I

Schemat 1. Algorytm wyszukiwania sekwencyjnego z „wartownikiem” (b) i bez (a). N - liczba elementów tablicy, tab[] - tablica, X - element do odnalezienia

Schemat 2. Algorytm wyszukiwania binarnego. N - liczba elementów tablicy, tab[] - tablica, X - element do odnalezienia.

N, tab[], X

L=0; P=N;

L<P

S=(L+P)/2

tab[L]==X

tab[S]==X

Wynik:

S

N

T

T

N

tab[S]<X

T

N

L=S+1

P=S

I

I++

X==tab[I]

I=0

N, tab[], X

N

T

a) b)

N

T

T

Wynik:

L

N

Wynik:

N

---