Akademia Górniczo-Hutnicza

im. Stanisława Staszica w Krakowie

Metody numeryczne i statystyka dla inżynierów

laboratorium

Temat:

Metoda Newtona

Grupa laboratoryjna:

7b

Sprawozdanie wykonał:

Krupnik Piotr

1. Funkcja rozpatrywana w sprawozdaniu:

y = -x² + 3x + 4

x₁ = -1

x₂ = 4

2. Interpretacja geometryczna metody Newtona:

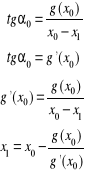
Stąd wzór iteracyjny:

3. Implementacja metody Newtona w programie matlab:

P = [-1 3 4]; (wektor współczynników funkcji y)

dP = polyder(P); (wektor współczynników pochodnej funkcji y)

k=5; (punkt początkowy - x₀)

dokl=0.1; (dokładność wyniku)

x=-2:0.1:5;

plot(x,polyval(P,x));

grid;

xlabel('x');

ylabel('y');

n=0;

while abs(polyval(P,k))>=dokl

k=k-(polyval(P,k)/polyval(dP,k));

n=n+1;

end

k (wynik)

n (ilość wykonań pętli koniecznych do otrzymania wyniku dla określonej dokł.)

4. Wyniki wyświetlane przez program przy różnych określonych dokładnościach:

• dokl = 0.1000:

k = 4.0076

n = 4

• dokl = 0.0100:

k = 4.0000

n = 5

• dokl = 1.0000e-005

k = 4.0000

n = 6

5. Wnioski:

W zakresie dużych przybliżeń ich zmiana powoduje zwiększenie dokładności wyniku, jednak dla pewnego odpowiednio małego przybliżenia dalsze zwiększanie dokładności nie wpływa na otrzymany wynik. Dlatego warto określać możliwie małą dokładność dla uzyskania wyniku z satysfakcjonującym przybliżeniem przy jednoczesnej oszczędności czasu działania programu.

1