Ruch po okręgu; siły zmienne; praca wykonana przez siły; rodzaje energii

1. Dynamika ruchu jednostajnego po okręgu - siła dośrodkowa

2. Układy nieinercjalne i pseudo-siły

3. Siły zmienne; siły zależne od czasu: metody analityczne

4. Siły hamujące i ruch obiektów podczas spadku swobodnego w powietrzu

5. Praca wykonana przez stałą siłę na danym obiekcie

6. Praca wykonana przez siłę zmienną: przypadek jednowymiarowy

7. Siła sprężystości

8. Energia kinetyczna oraz praca jako rodzaj energii; moc

9. Siły zachowawcze i niezachowawcze

10. Energia potencjalna

******************************************************************************

1. Dynamika ruchu jednostajnego po okręgu - siła dośrodkowa

W1: W ruchu jednostajnym po okręgu, działa przyspieszenie dośrodkowe (a_cp):

• Wielkość: a_cp = ²r (lub: v²/r), [ω =
  = prędkość kątowa]

• Kierunek: a_cp jest zawsze skierowane w kierunku centrum okręgu.

Zgodnie z II-gą zasadą dynamiki Newtona: na ciało działa siła: F_cp = m²r.

N1: F_cp = siła dośrodkowa (z ang. centripetal); kierunek F_cp ≡ kierunek a_cp.

(1) (2)

2. Nieinercjalne układy odniesienia (NUO) i pseudo-siły

Mówiąc dokładnie, każde laboratorium na Ziemi jest układem nieinercjalnym, a więc jako taki nie może spełniać zasad dynamiki Newtona. Biorąc pod uwagę 2ZD - jeśli zmierzymy przyspieszenie na Ziemi, zależność F = m a, w niektórych wypadkach nie jest ściśle poprawna.

⇒ Aby zastosować mechanikę klasyczną dla układu nieinercjalnego musimy zastosować dodatkowe siły, które nazywane są pseudo-siłami.

Więcej na temat układów inercjalnych: [zob., H/R/W s. 147]

• Wielkości fizyczne można podzielić na dwa rodzaje:

• { m, F, a, t } maja te same wartości w różnych inercjalnych układach odniesienia (IUO) → wielkości te są niezmiennicze;

• { v, E_kin, W(praca) } mają różne wartości w różnych IUO.

• Zasada niezmienniczości:

wszystkie prawa fizyki są identyczne (tj. mają tą samą postać) we wszystkich układach inercjalnych.

Np. 2ZD: F = m a (prawdziwa we wszystkich IUO!); lecz nie stosuje się jej dla NUO!

Podstawowe zasady dotyczące nieinercjalnych układów odniesienia i pseudo-sił:

• Inercjalne układy odniesienia (IUO) = poruszające się względem siebie ze stała prędkością (tj. wzdłuż linii prostej ze stałą szybkością); np.: stacjonarny obserwator na powierzchni Ziemi i obserwator w pociągu poruszającym się z v = const.

• Prawa Newtona stosują się wyłącznie dla ciał poruszających się w IUO.

• Nieinercjalne układy odniesienia (NUO) = poruszające się względem siebie z pewnym niezerowym przyspieszeniem; np.: stacjonarny obserwator na powierzchni Ziemi i w jednostajnym ruchu po okręgu.

• Jeśli zdefiniujemy “rzeczywiste” siły, jako siły reprezentujące oddziaływanie ciała z otoczeniem, żeby odróżnić “rzeczywiste” siły od tzw. sił “inercjalnych” (tj. sił bezwładności) obserwowanych w NUO używamy: “pseudo-sił” lub inaczej “sił pozornych“.

• Przykłady pseudo-sił: [zob., Serway, s.135]

• Siła odśrodkowa F_cf (z ang. centrifugal = odśrodkowa) = reakcja ciała poruszającego się ruchem jednostajnym po okręgu obserwowana w NUO, wywołana działaniem przyspieszenia dośrodkowego a_cp.

N2: Siła odśrodkowa zależna jest od odległości od osi obrotu.

• Siła Coriolisa jest siłą inercjalną działającą na, np.:

a) obiekty poruszające się na Ziemi z północy ⇔ południe

→ np. rzeki płynące w kierunkach Płn./Płd. lub Płd./Płn. meandrują,

b) obiekty poruszające się na okrągłej platformie - jeżeli są obserwowane w

ramach NUO !

N3: Siła Coriolisa zależy od prędkości i kierunku w stosunku do osi obrotu.

3. Siły zmienne; siły zależne od czasu: metody analityczne

Ogólnie, siły nie są stałe, lecz mogą się zmieniać wraz z (lub zależą od):

• czasem, np., prowadzenie samochodu lub drżenie rąk (!).

• prędkością, np., lepkość [w płynach].

• położenia, np., siła sprężystości [ F = -kx].

Metoda analityczna: znając siłę całkowitą F(t), możemy obliczyć przyspieszenie a(t):

• Ponieważ a = dv/dt, prędkość v(t) można obliczyć przez scałkowanie:

, Pyt: Jakie są granice całkowania?

gdzie v_o, jest prędkością początkową. A:

• 
  
  
  Ponieważ v = dx/dt, położenie x(t) można obliczyć przez scałkowanie, jeśli znana jest prędkość v(t).

,

gdzie x_o położenie początkowe.

⊳⊳ Narysuj i zanalizuj v(t)
: ⇒

(a) dla v_o = const

(b) dla v_o = 0 i a = const

(c) ogólnie v(t)

⊳⊳ Narysuj a(t) dla a = const ⇓

4. Siły hamujące i ruch obiektów podczas spadku swobodnego w powietrzu

Siły hamujące (przykład: opór powietrza lub wody) zawsze działają w kierunku przeciwnym do kierunku prędkości, a ich wartość zależy od wartości prędkości. Dlatego przyspieszenie wywołane siłami hamowania będzie funkcją prędkości.

Zakładając że na obiekt o masie m opadający

w powietrzu działa siła hamująca D, która

zwiększa się liniowo wraz z prędkością, mamy:

(D ~ ν) D = bv.

Obiekt o masie m jest zrzucony będąc w spoczynku:

Oblicz prędkość v(t) jako funkcję czasu.

Wybierzmy punkt zrzutu jako początkowy i oś y skierowaną w dół. Obiekt porusza się pionowo w dół. Pionowa składowa siły (używając 2ZD) to:

mg − bv = ma or a = g − (b/m)v.

Zauważmy, że skoro v zwiększa się to kiedyś obiekt osiąga stan gdzie przyspieszenie jest zerowe. W takiej sytuacji prędkość będzie niezależna od upływającego czasu. Warunek ten definiuje prędkość końcową: v_t.

⊳⊳ Znajdź prędkość v_t dla której a = 0 ⇒

Żeby znaleźć ogólną zależność v(t), na początek należy zapisać:

a(v) = dv/dt or dv/dt = g − (b/m)v

⇒
.

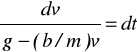
Teraz można to bezpośrednio scałkować:

.

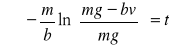
N1: Istnieje bardziej skomplikowana doświadczalna zależność: D = ½ C ρAv²

C - współczynnik hamowania; A - powierzchnia przekroju poprzecznego ciała;

ρ - gęstość powietrza; v - prędkość względna. [H/W/R, s.114]

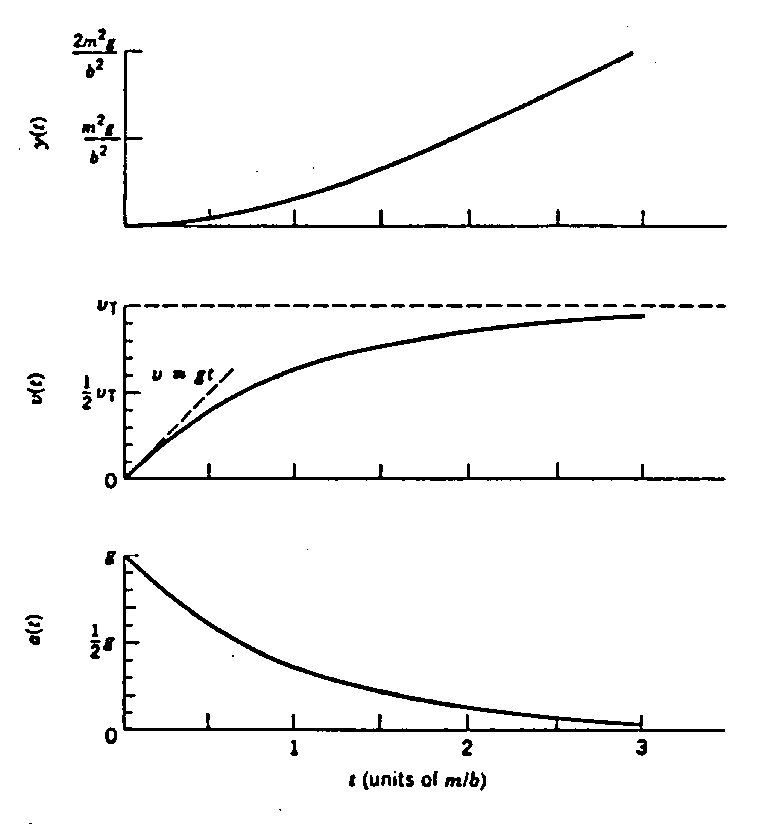
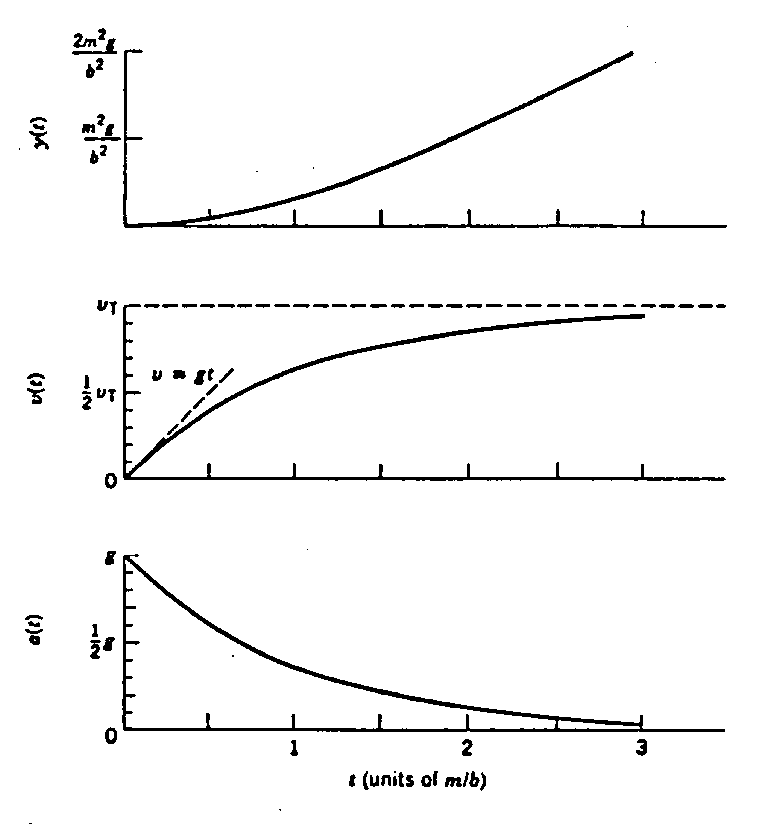
Analiza v(t):

(A) Dla małego odcinka t :

. ⊳⊳ Oblicz sam ⇒

W tym czasie, prędkość jest niewielka. Siła hamująca jest także mała, a więc może zostać pominięta. Wtedy przyspieszenie skierowane w dół wynosi g.

(B) Dla długiego odcinka t, v(t) dąży ekspotencjalnie do zera (e^-x → 0 gdy x → ∞).

Szybkość zbliża się do prędkości końcowej v_t Zobacz diagram v(t) poniżej.

Tabela 2. Prędkości końcowe obiektów w powietrzu.

Obiekt	Prędkość końcowa (m/s)	95% Dystans (m)
15-funtowy pocisk		145	2500
Skydiver (typowo)		60	430
Piłka baseballowa		42	210
Piłka tenisowa		31	115
Piłka koszykowa		20	47
Piłka ping-pongowa		9	10
Kropla deszczu (promień=1.5mm)		7	6
Spadachroniarz (typowo)		5	3

5. Praca wykonana przez stałą siłę na danym obiekcie

Gdy stała siła F działa na cząstkę, cząstka porusza się wzdłuż linii prostej w kierunku zgodnym z kierunkiem działającej siły → przemieszczenie s.

Praca W wykonana przez tą siłę na cząsteczce, definiowana jest jako iloczyn wielkości siły F i wielkości przemieszczenia s wzdłuż którego działa ta siła:

W = Fs.

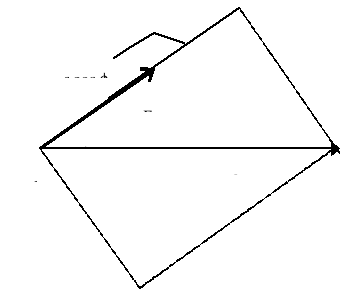
Ogólnie, cząstka może się poruszać w innym kierunku. W takim wypadku, praca wykonana przez na cząsteczce, przez siłę F jest iloczynem wielkości składowej siły w kierunku ruchu i wielkości przemieszczenia s. Jeśli siła F tworzy kąt  z kierunkiem przemieszczenia cząsteczki s, wtedy zgodnie z definicją:

W = (F cos)s. [zob. lewy rys.] ; W = F (s cos). [zob. prawy rys.]

Druga interpretacja - równanie prawe na wykonaną pracę oznacza, że możemy obliczyć pracę przez wymnożenie wartości siły przez składową przemieszczenia w kierunku działającej siły.

Ogólna definicja pracy: praca jest skalarem → W jako iloczyn skalarny:

= F.s Jednostka pracy w układzie SI: 1 niuton.metr = 1 dżul: [N.m] = [J]

Całkowita praca = praca wykonana przez wypadkową siłę.

Np.: dla trzech sił: lewa strona: W = W₁ + W₂ + W₃ = {prawa strona}

Gdy na ciało działa więcej niż jedna siła, praca wykonana przez

każdą siłę może być przedstawiona przy użyciu tej samej definicji.

Poniższy diagram przedstawia całą procedurę.

Lewa strona równania Prawa strona równania

6. Praca wykonana przez siłę zmienną w 1D:

Dla przypadku 3-D: F(x, y, z); dla 1-D:
(x) = F₁(x)

δW₁ = F₁ δx₁ {zobacz diagram } ⇒

N1: ∑ po interwałach

⇒ W = lim ∑
x_j =

Δx→0

N2: W wąskim zakresie (dla `paseczka'): W_j =
x_j

N3:
= średnia wartość F(x) w j-tym interwale

N4: Definicja: praca dodatnia i ujemna (W):

(+) W = energia dostarczona do obiektu przez siłę zewnętrzną

(-) W = energia oddana przez obiekt

7. Siła sprężystości {zobacz diagram } ⇒

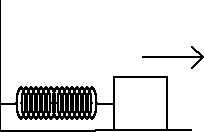
Rozważmy bloczek dołączony do sprężyny:

Gdy bloczek zostanie przemieszczony z położenia gdy sprężyna jest rozluźniona, do położenia x , sprężyna działa siłą F_s (siłą przywracającą) na bloczek. Siłę tą można opisać z dobrym przybliżeniem przy pomocy zależności:

,

Gdzie k jest dodatnia stałą nazywaną współczynnikiem sprężystości sprężyny. Jeśli końcowym położeniem obiektu jest x_f, wtedy praca wykonana przez sprężynę na bloczku:

.

Z drugiej strony, praca wykonana przez siłę zewnętrzna F_ext (równą co do wartości F_s lecz przeciwnie skierowaną) wynosi:

(z ang. external = zewnętrzna)

.

8. Energia kinetyczna (EK) oraz praca jako rodzaj energii; moc

Cząstka o masie m porusza się z prędkością v:

jej energia kinetyczna K jest:
.

Gdy wypadkowa siła F_net (z ang. net force = siła wypadkowa) działa na cząstkę i cząstka jest w ruchu, siła wypadkowa wykona pewną pracę na cząsteczce. Ażeby zmierzyć tą pracę rozważmy w jaki sposób prędkość v cząstki zmienia się w czasie t i z odległością x. Procedura:

(1) Równanie dla pracy wykonanej przez siłę zmienną w przypadku 1-D:

(2) Zapisać F_net przy pomocy v i x :

Praca wypadkowa (z ang. net work) wykonana przez wszystkie zewnętrzne siły:

Używając ten wynik, twierdzenie o relacji praca-energia można sformułować jako:

Wypadkowa praca wykonana przez siły działające na cząstkę jest równa zmianie energii kinetycznej tej cząstki.

⇒ W_net = K_f - K_i = Δ K

N2: Relacja praca-energia ma zastosowanie tylko dla cząstek. Dla rzeczywistych obiektów, część energii może zostać zmieniona na energię wewnętrzną (tzw. energia “cieplna”): K_f = K_i + W

Moc - dwie definicje:

(1) Dla układów mechanicznych, moc jest zdefiniowana jako szybkość z jaką praca została wykonana:

⇒ Chwilowa moc P dostarczona przez “pośrednika” energii:

⇔ chwilowa szybkość wykonania pracy

⇒ Średnia moc będąca wynikiem siły wykonującej pracę na obiekcie w czasie Δt: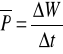

(2) Ogólniej, moc jest zdefiniowana: (2a) jako energia dostarczona w jednostce czasu LUB (2b) jako szybkość z jaką energia jest przetransferowana przez siłę z jednej formy w drugą:

⇒ Moc chwilowa:
; ⇒ Moc średnia: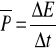

ΔE (dE) - ilość energii przetransferowanej w czasie Δt (dt)

Mając daną moc, możemy wydedukować jaka praca została wykonana przez ”pośrednika”:

W = Pt

W układzie jednostek SI jednostką mocy jest:

dżul na sekundę = 1 wat (skrót W) ⇒ [J/s] = [W]

Praca (energia) także może być wyrażona w jednostkach mocy × czas. Stąd pochodzi jednostka kilowatogodziny używana przez firmy z branży energetycznej.

9. Siły zachowawcze i niezachowawcze

Przykład 1: Siła sprężysta:
{zobacz diagram w Cz. 7}

⇒ Cykle: (1) rozciąganie (zewnętrzne) oraz (2) kurczenie się (naturalne = puszczamy sprężynę)

(1) Rozciąganie: Praca sprężyny < 0: (2) Kurczenie się (ściąganie): praca sprężyny > 0:

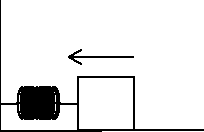
blok = obiekt

x=0 ↑ x=0 ↑ (bez tarcia !)

Z definicji: Jeśli energia jest przetransferowana do obiektu ⇒ W jest obrana jako (+)

(1) Rozciąganie: ⇒ praca wykonana przez sprężynę jest ujemna:

⇒ praca wykonana przez zewnętrzną siłę jest dodatnia:

[Ta praca została zamieniona na elastyczną energię potencjalną zgromadzoną w sprężynie]

(2) Kurczenie się: ⇒ praca wykonana przez sprężynę na bloku jest dodatnia:
.

Pyt.: Dlaczego w kroku (2) W(sprężyny >0? Odp.: Ponieważ zwiększa się energia kinetyczna bloku.

Pyt.: W powyższym przypadku, skąd pochodzi przetransferowana energia?

Odp.: Z elastycznej energii potencjalnej zgromadzonej przez sprężynę w kroku (1).

W = 0 dla całego cyklu !

Przykład 2: Siła tarcia kinetycznego (F_kf):

⇒ przesuwanie bloku po podłożu przeciwko F_kf (ang. kinetic friction = tarcie kinetyczne)

Krok 1: Praca wykonana przez tarcie < 0. Krok 2: Praca wykonana przez tarcie < 0.

N1: Siła tarcia kinetycznego F_kf spowalnia blok poprzez zamianę energii E_kin bloku w ciepło tego bloku/podłoża ⇒ praca W wykonana przez siłę F_kf na bloku jest zawsze ujemna: (-)W(F_kf)

W ≠ 0 dla całego cyklu !

Siły zachowawcze a siły niezachowawcze:

Def. 1: Jeżeli ciało pod wpływem siły porusza się po drodze zamkniętej, i ciało to nie wykonało żadnej pracy (praca = siła × przesunięcie) to siła jest zachowawcza; w innym wypadku jest ona niezachowawcza.

Siły zachowawcze: siła sprężystości; siła grawitacji

Siły niezachowawcze: siła tarcia kinetycznego

Def. 2: Jeżeli praca wykonana przez siłę, jest powodem przesunięcia obiektu z położenia początkowego do końcowego, i jest ona niezależna od drogi po jakiej odbyło się to przesunięcie, wtedy siła wykonująca tą pracę jest zachowawcza; w innym wypadku jest ona niezachowawcza.

10. Energia potencjalna (EP)

• EP zależy od względnego położenia lub wzajemnej orientacji części układu.

• EP nie zależy od prędkości lub historii układu.

• Koncepcja energii potencjalnej może zostać zastosowana wyłącznie w przypadku sił zachowawczych. Nie można jej stosować dla sił niezachowawczych.

DEF: Zmiany energii potencjalnej ΔU odpowiadające częściowej zmianie konfiguracji są ujemne w stosunku do pracy wykonanej przez siły zachowawcze (W):

ΔU = − W, ⊳⊳ Rozważ zmianę EP

spowodowaną przeniesieniem ciała z h₁ to h₂ ⇒

W poprzednim równaniu, wybraliśmy energię potencjalną w
jako punkt odniesienia: ⇒ energia potencjalna = 0 w tym punkcie !.

Odp: mg (h₂ - h₁) = Δ U; W = F (h₁ - h₂) = - F (h₂ - h₁)

Ćwiczenia 2

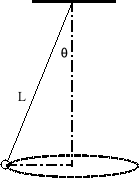
1. Kula zawieszona jest na sznurku o długości L i odchylona z położenia równowagi (zobacz lewy rysunek poniżej). Kula jest ustawiona do ruchu po poziomym okręgu (promień = L sinθ). Narysuj diagram ciała swobodnego dla kuli. Oblicz wypadkową siłę działającą na kulę oraz prędkość kątową (ω) dla ruchu po okręgu.

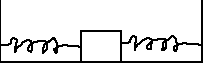
2. Rozważ dwie identyczne sprężyny dołączone do obiektu (zobacz prawy diagram powyżej). Obydwie sprężyny mają współczynnik sprężystości k i początkowy naciąg x_o. Rozważ dalsze przemieszczenie x na prawo od położenia początkowego. Narysuj diagram ciała swobodnego dla tego obiektu oraz:

(1) siłę wypadkową jaką działają na obiekt obydwie sprężyny,

(2) całkowitą pracę wykonaną przez sprężyny.

3. Klimatyzator o mocy jednego konia mechanicznego (746 W) był włączony bez przerwy przez trzy miesiące. Oblicz zużytą energię w dżulach i kilowatogodzinach.

(przyjmij, że jedna kilowatogodzina kosztuje ok. 0.30 zł.)

4. Jak dużo energii potencjalnej można zgromadzić w sprężynie (stała sprężystości k, rozciągnięcie x)? Jaka część tej energii może zostać zamieniona na pracę?

Wstęp do fizyki: Wykład + ćwiczenia 2 Prof. C. Rudowicz 2012/13

Page2

Wstęp do fizyki: Wykład + ćwiczenia 2 Prof. C. Rudowicz 2012/13

Page 7

N1: Stała b zależy od wielkości i kształtu obiektu.

N2: b także zależy od gęstości i lepkości cieczy (gazu).

Objaśnienia wykresów:

y(t):

v(t): v_t

½ v_t

linia prosta jest

przybliżeniem: v = gt

a(t): g

½ g

t (w jednostkach m/b)

⊳⊳ Praca domowa: opracuj krok po kroku wszystkie wyprowadzenia (używając odpowiednich obliczeń)

Wskazówka - użyj: e^x ≈ 1 + x

[H/W/R, s.114, Tabela 6-1]

Dystans ≡ odległość na którą ciało spada, zaczynając ze stanu spoczynku do momentu osiągnięcia 95% swojej prędkości końcowej (v_t)

y(t):

v(t): v_t

½ v_t

linia prosta jest

przybliżeniem: v = gt

a(t): g

½ g

t (w jednostkach m/b)

⊳⊳ Objaśnienia wykresów:

Odp: Od t_p (początkowy czas) do t_k (końcowy

czas); a(t) działa pomiędzy t_p & t_k (!)

h₂ ΔU =

W =

h₁

_h

⊳⊳ Zidentyfikuj siłę dośrodkową: F_cp na diagramach (L) & (P).

Odp: L: F_cp = napięcie w sznurze; P: F_cp = tarcie pomiędzy oponami a powierzchnią drogi

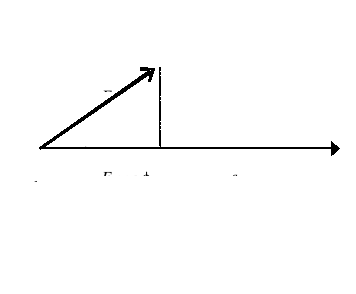
⊳⊳ Wpisz poniżej lewą i prawą stronę równania dla tego diagramu:

Prawo Hooke'a

ujemna W !

dodatnia W !

N1: Jeśli nie ma zmian innych form energii !

N1: Stosuje się gdy moc

jest stała w czasie !

---