Matusz Jurecki 14.04.2005

MDB I

Gr. 63

Sprawozdanie z ćwiczenia nr 6.

Temat: Pomiar siły Coriolisa

1. Zagadnienia teoretyczne.

Położenie jakiegokolwiek ciała, z którym można związać układ współrzędnych przyjęty za układ odniesienia.

Wyróżniamy dwa układy odniesienia:

• inercjalny

• nieinercjalny

Układ inercjalny jest to taki układ, który porusza się jednostajnie i prostoliniowo względem nieruchomego lub poruszającego się ze stałą prędkością układu odniesienia.

Układ nieinercjalny jest to taki układ, który porusza się względem układu inercjalnego z przyśpieszeniem. W nieinercjalnych układach działają siły bezwładności.

Siła Coriolisa jest siłą bezwładności pojawiającą się w obracających układach, a więc występuje w układzie nieinercjalnym.

Przyśpieszenie Coriolisa a_{c =} 2 ⋅ ω × V występuje, gdy ciało porusza się z prędkością V znajduje się w obracającym układzie odniesienia (V - jest to prędkość ciała względem układu obracającego się). Wektor przyśpieszenia a_c jest prostopadły do osi obrotu (ω) oraz do prędkości ciała (V).

Wyróżniamy dwa sposoby opisu zjawisk zachodzących w wirujących układach odniesienia:

a). Opis z punktu widzenia obserwatora ruchomego (związanego z układem) - rozpatrujemy 2 ruchy (jednostajny i jednostajnie przyśpieszony po łuku.

Droga po łuku ⇒
czyli a_c =
, t =
więc a_c =

b). Opis obserwatora nieruchomego względem układu - zgodnie z pierwszą zasadą dynamiki ciało porusza się jednostajnie po lini prostej czyli droga równa jest R , a t =
, ale tarcza się obraca, w związku z tym zmienia się kąt
,
, a_c = 2V

F_c = m ⋅ a_c czyli a_c =

2). Wykonanie ćwiczenia.

• ustawić koniec równi na osi obrotu tarczy,

• położyć na tarczy krążek papieru, tak aby położona na jej wierzchu kalka była zwrócona stroną rysującą do dołu,

• włączyć gramofon do sieci,

• puścić kulkę z górnego końca równi,

• zmierzyć wysokość równi h w punkcie, gdzie kulka zaczyna staczać się i zasady zachowania energii obliczyć prędkość liniową kulki na poziomie tarczy. Po zdjęciu papieru z tarczy jest na nim ślad kuli w postaci odcinka paraboli. Z punktu O wykreślamy dwa odcinki: R - styczny do toru, R₁ - łączy początek i koniec śladu. Kąt między tymi prostymi jest równy
  ,

• Pomiary należy powtórzyć dla innego kąta nachylenia równi,

• Otrzymane wartości wstawić do wzoru,

• Pomiary powtórzyć dla innej kuli,

3). Tabela.

Lp.	h	V	R		ac	m	Fc	Fc
	[m]	[m/s]	[m]	[rad]	[m/s^2]	[kg]	[N]	[N]
1.	0,05	0,58	0,2	1,05	3,53	0,190	0,67	± 0,22
2.	0,05	0,58	0.2	1,12	3,03	0,190	0,71
3.	0,05	0,58	0,2	1,09	3,70	0,190	0.70
4.	0,05	0,58	0,2	0,94	3,16	0,230	0,73
5.	0,05	0,58	0,2	0,96	3,23	0,230	0,74
6.	0,05	0,58	0,2	0,98	3,30	0,230	0,76

4). Obliczenia.

Aby przeliczyć stopnie na radiany stosuję wzór: t
=

60°=1,05 rad, 64°=1,12 rad, 63°=1,09rad

54°=0,94 rad, 55°=0,96 rad, 56°=0,98 rad

Aby wyliczyć V wykorzystuję zasadę zachowania energii:

mgh =

gdzie: J =
,a

czyli: mgh =
, po skróceniu przez m otrzymujemy:

gh =

gh =
⇒ V² =

więc : V =
gdzie: g - uważam za stałą równą g = 9,81

V=
=0,58

Teraz wyliczam a_c =

a₁ =

a₁=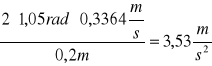

a₂ = 3,03

a₃= 3,70

a

a

a

F_c=

F₁ =

F₂ = 0,71

F₃ = 0,70

F₄ = 0,73

F₅ = 0,74

F₆ = 0,76

ΔV=
=0.018

ΔV=0,018

ΔF_c = ΔF_c=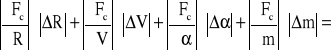
ΔF_c=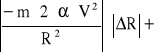



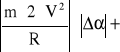
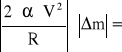
0,0034 + 0,041+ 0,0064 + 0,177 =0,22

Δm = 0,005 kg, Δr = 0,005 m, ΔR = 0,001 m, Δα = 0,01 rad, Δh = 0,001 m

---