Tatiana Zaszkowska 14 III 2001

Ćwiczenie nr 15

Temat: Wyznaczanie lepkości cieczy metodą Stokesa.

Tabela wyników:

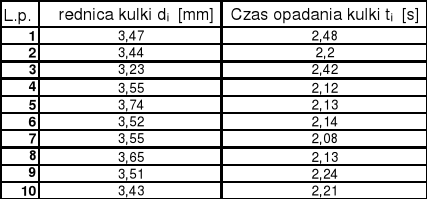
Odległość l=0,6m

Gęstość ołowiu

Gęstość badanej cieczy

Przyspieszenie ziemskie

Teoria zjawiska:

Jeżeli w dwóch stykających się ze sobą warstwach płynów rzeczywistych prędkości przepływającego płynu są różne, to obserwujemy stan przejściowy, podczas którego zachodzą procesy dążące do wyrównania prędkości w obu warstwach. Procesy te noszą nazwę tarcia wewnętrznego lub lepkości i mierzone są ilościowo współczynnikiem lepkości.

Rozpatrzmy warstwę cieczy o grubości h, ograniczoną dwiema płaszczyznami. Od strony warstwy poruszającej się szybciej działa na warstwę poruszającą się wolniej siła przyspieszająca. Natomiast od strony warstwy poruszającej się wolniej na warstwę poruszającą się szybciej działa siła hamująca. Siły te, zwane siłami tarcia wewnętrznego, skierowane są stycznie do powierzchni warstw. Siła tarcia wewnętrznego F_T jest tym większa, im większe jest pole powierzchni S oraz im większy jest gradient prędkości w kierunku prostopadłym do ruchu. Dla większości cieczy spełniona jest zależność:

Ciecze spełniające powyższe równanie nazywamy cieczami newtonowskimi. Współczynnik lepkości jest liczbowo równy wartości siły stycznej, która przyłożona do jednostkowej powierzchni przesuwanej warstwy utrzymuje w tej warstwie przepływ laminarny ze stałym jednostkowym gradientem prędkości warstw:

.

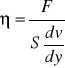
Współczynnik ten odnosi się do tak zwanej lepkości dynamicznej w odróżnieniu od współczynnika lepkości kinetycznej:

,

gdzie
- gęstość cieczy.

W gazach zjawisko lepkości polega na przekazywaniem pędu przez cząsteczki warstwy o większej prędkości cząsteczkom z warstwy wolniejszej. Na skutek ruchów cieplnych zachodzi przemieszczanie się cząsteczek z większymi pędami do warstw z mniejszymi pędami. Dlatego też zmianie ulegają prędkości warstw. Na każdą z warstw działa odpowiednio siła przyspieszająca i hamująca, która wiąże się ze zmianą pędu.

Lepkość cieczy w znacznym stopniu zależy od temperatury; ze wzrostem temperatury jej wartość maleje. Zmiany temperaturowe lepkości gazów mają charakter odwrotny-lepkość gazu wzrasta wraz z temperaturą.

Współczynnik lepkości cieczy newtonowskich maleje wraz ze wzrostem temperatury zgodnie z zależnością:

,

gdzie A,B - stałe.

Dla gazów słuszny jest wzór:

,

gdzie
- średnia prędkość związana z chaotycznym ruchem cząsteczek,
- średnia droga swobodna, K - stała gazowa. Zatem współczynnik lepkości gazu zależy wprost proporcjonalnie od temperatury T.

Opis metody:

WISKOZYMETR STOKESA

Przy małych prędkościach kulki siła oporu jest bezpośrednio uwarunkowana lepkością cieczy. Warstwa cieczy przylegająca bezpośrednio do jej powierzchni pociąga za sobą warstwę następną, lecz jej prędkość jest mniejsza. Kolejne warstwy mają jeszcze mniejsze prędkości, co jest wynikiem działania sił tarcia wewnętrznego.

Na opadającą kulkę działają następujące siły: siła ciężkości F_G, siła wyporu F_W (prawo Archimedesa) i siła oporu F_O (prawo Stokesa) skierowane przeciwnie niż siła ciężkości. Sumujemy wszystkie siły działające na kulkę:

Początkowo kulka porusza się ruchem przyspieszonym. Od pewnego momentu siły równoważą się (F=0), czyli z I zasady dynamiki kulka porusza się ruchem jednostajnym. Uwzględniając
otrzymujemy:

Wykonane czynności:

1. Dziesięć kulek zmierzono mikromierzem.

2. Zmierzono odległość l od górnego pierścienia do dolnego.

3. Wrzucano kolejno kulki do kolumny i mierzono czas t przebycia drogi l.

4. Współczynnik lepkości wyznaczamy z powyższego wzoru.

Obliczenia:

Podstawiając kolejno wielkości z tabeli wyników do wzoru i uzgadniając jednostki otrzymujemy:

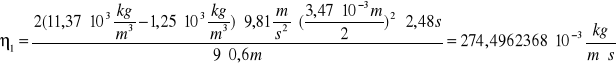
Wartość średnia współczynnika lepkości jest równa:

Niepewność pomiaru:

NIEPEWNOŚĆ POMIARU ŚREDNICY KULKI

Odchylenie standardowe średniej:

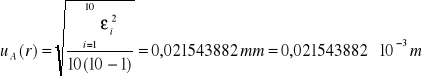
Odchylenie standardowe śruby mikrometrycznej:

Niepewność całkowita:

NIEPEWNOŚĆ POMIARU CZASU

Odchylenie standardowe średniej:

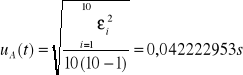
Odchylenie standardowe stopera:

Niepewność całkowita:

NIEPEWNOŚCI DLA POZOSTAŁYCH WIELKOŚCI

Niepewność całkowita dla
:

Niepewność całkowita dla
:

Niepewność całkowita dla g:

Niepewność całkowita dla l:

NIEPEWNOŚĆ CAŁKOWITA DLA WSPÓŁCZYNNIKA LEPKOŚCI

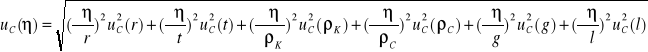
Wartości pochodnych cząstkowych dla kulki nr 9 o promieniu r=1,755mm i czasu t=2,24s.

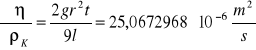
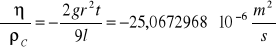
Podstawiając wszystkie wartości otrzymujemy:

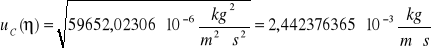
Wyprowadzenie jednostki:

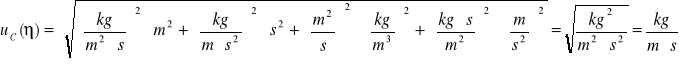
Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wynik pomiaru:

Opis metody:

WISKOZYMETR HOPPLERA

W wiskozymetrze Hopplera średnica cylindra tylko nieznacznie przekracza średnicę kulki, a sam cylinder jest ustawiony nieco ukośnie, dzięki czemu kulka toczy się po ściance cylindra ruchem jednostajnym. Wzór na lepkość stosowany wyżej można teraz zapisać inaczej:

,

gdzie K jest stałą przyrządu wyznaczaną doświadczalnie z pomiaru dla cieczy o znanym współczynniku lepkości. Wynika to z następujących zależności. Siła opory ze strony cieczy jest proporcjonalna do prędkości toczenia się kulki:

,

gdzie k - współczynnik proporcjonalności stały dla danego przyrządu. Rozkładając siły ciężkości i wyporu na składowe styczne i normalne otrzymamy warunek równowagi sił:

.

Skąd mamy:

.

Uwzględniając prędkość ruchu jednostajnego
otrzymamy
.

Pomiar czasu opadania kulki można powtarzać wielokrotnie przez obrócenie przyrządu o 180⁰ wokół osi. Cylinder wiskozymetru otoczony jest płaszczem wodnym o regulowanej temperaturze, której wartość wskazuje termometr.

Tatiana Zaszkowska 14 III 2001

Ćwiczenia nr 16

Temat: Wyznaczanie lepkości cieczy za pomocą wiskozymetru Hopplera.

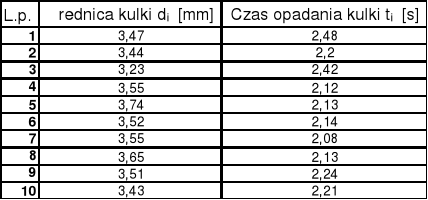
Tabela wyników:

Gęstość kulki

Gęstość cieczy w temperaturze T

Stała kulki

Temperatura początkowa

Temperatura końcowa

Wykonane czynności:

1. Wypoziomowano przyrząd i odczytano temperaturę T₁.

2. Po obróceniu naczynia i opadnięciu kulki ustawiono urządzenie w pozycji początkowej i zabezpieczono przed poruszaniem.

3. Sekundomierzem zmierzono czas toczenia się kulki na określonym odcinku drogi.

4. Poczyniono dziesięć takich prób i odczytano temperaturę T₂.

Obliczenia:

Średnia temperatura:

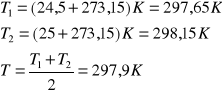
Tej temperaturze odpowiada gęstość cieczy

Średni czas opadania kulki:

Lepkość cieczy:

Niepewność pomiaru:

NIEPEWNOŚĆ POMIARU CZASU

Odchylenie standardowe średniej:

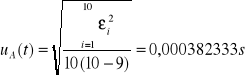
Odchylenie standardowe stopera:

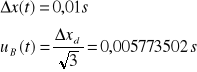
Niepewność całkowita:

NIEPEWNOŚCI DLA POZOSTAŁYCH WIELKOŚCI

Niepewność całkowita dla K:

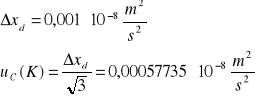
Niepewność całkowita dla
:

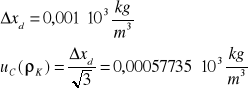
Niepewność całkowita dla
:

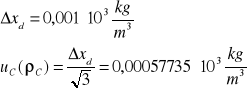
NIEPEWNOŚĆ CAŁKOWITA DLA WSPÓŁCZYNNIKA LEPKOŚCI

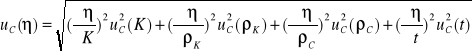
Wartości pochodnych cząstkowych:

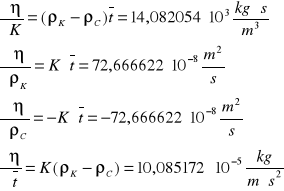
Podstawiając wszystkie wartości otrzymujemy:

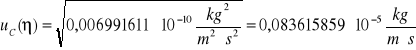
Niepewność rozszerzona (dla
k=2) wynosi:

Zaokrąglając niepewność rozszerzoną do dwu cyfr znaczących otrzymujemy wynik:

Wnioski:

Wyznaczanie lepkości metodą Stokesa nie jest zbyt efektywne. Może o tym świadczyć na przykład wysoki błąd pomiaru. Kulka w cylindrze opada z dość dużą prędkością, zaś jej rozmiary są małe, zatem trudno jest zauważyć, kiedy kulka mija oznaczone miejsca i tym samym trudno dokładnie zmierzyć czas przebytej drogi. Zależy to tylko i wyłącznie od refleksu studenta.

Promień kulki w stosunku do promienia cylindra jest bardzo mały, zatem możemy zaniedbać wpływ ścianek na tarcie wewnętrzne warstw cieczy.

Mogłoby się wydawać, że czas opadania kulek zależy odwrotnie proporcjonalnie od ich wielkości (im większa kulka tym szybciej opada), ale pomiary nie potwierdziły tego.

W cylindrze mogą nastąpić zakłócenia ruchu spowodowane na przykład drganiami podłoża - stołu.

Wnioski:

Wyznaczanie lepkości cieczy wiskozymetrem Hopplera jest o wiele bardziej dokładne niż z zastosowaniem metody Stokesa. Urządzenie ma lepszą konstrukcję, a kulka zbliżone rozmiary do wewnętrznej rurki. Dzięki czemu można lepiej zaobserwować moment mijania kulki linii wyznaczających odcinek drogi i dokładniej zmierzyć czas.

W celu uniknięcia zakłóceń ruchu rurka wychylona jest od pionu o pewien kąt oraz zabezpieczona sprężynowym zaczepem.

---