Spis treści:
1. Zakres i znaczenie Fizyki Budowli
2. Formy wymiany ciepła
3. Wymiana ciepła przez konwekcję
4. Wymiana ciepła przez promieniowanie
5. Złożona wymiana ciepła
6. Ruch ciepła przez przewodzenie.
7. Definicja przewodności cieplnej
8. Zależność współczynnika przewodzenia ciepła od gęstości objętościowej i
struktury materiału
9. Zależności współczynnika λ od zawartości wilgoci
10. Wpływ temp na wartość współczynnika λ.
11. Obliczeniowe wartości współczynnika λ
12. Jednowymiarowe ustalone przewodzenie ciepła
13. Dwukierunkowy przepływ ciepła
14. Obliczania przenikania ciepła przez przegrody zewnętrzne budynku.
15. Opór cieplny przegród ze szczelinami.
16. Obliczanie wartości temperatur ogrzewanych pomieszczeń w budynkach i
powietrza zewnętrznego.
17. Wymagania termoizolacyjne dla ścian, stropów i stropodachów.
18. Filtracja powietrza przez przegrody budowlane.
19. Komfort cieplny pomieszczeń
20. Zasady obliczania sezonowego zapotrzebowania na ciepło do ogrzewania
budynków
21. Składniki strat ciepła przy obliczaniu sezonowego zapotrzebowania
na ciepło do ogrzewania budynków
22. Składniki zysków ciepła przy obliczaniu sezonowego zapotrzebowania na
ciepło do ogrzewania budynków
23. Ciepłochłonność podłóg-zasady obliczania
24. Formy występowania wilgoci w materiałach budowlanych
25. Wilgotność powietrza
26. Przyczyny zawilgocenia przegród
27. Wilgoć z opadów atmosferycznych
28. Kapilarne podciąganie wody z gruntu
29. Wilgoć sorpcyjna
30. Zawilgocenie wskutek kondensacji pary wodnej
31. Zawilgocenie przegród w skutek dyfuzji i kondensacji pary wodnej
32. Obliczanie wewnętrznej kondensacji w ścianach zewnętrznych
33. Wysychanie przegród budowlanych z wilgoci początkowej
34. Ogólne wiadomości o dźwięku
35. Dopuszczalne poziomy dźwięków w pomieszczeniach
36. Wymagania izolacyjności akustyczna przegród i elementów
budowlanych
37. Obliczenie wskaźników jedno liczbowych izolacyjności od dźwięków
powietrznych
38. Obliczenie wskaźników jedno liczbowych izolacyjności od dźwięków
uderzeniowych
39. Podstawy teoretyczne izolacyjności akustycznej przegród budowlanych
40. Właściwości akustyczne przegród budowlanych
41. Właściwości akustyczne stropów
42. Charakterystyka światła. Widmo promieniowania
43. Wielkości świetlne promieniowana widzialnego
44. Kontrast luminacji i barw
45. Czynniki wpływające na oświetlenie dzienne oraz kryteria jego oceny
46. Wskaźniki orientacyjne wystarczającego oświetlenia dziennego
47. Określanie współczynnika oświetlenia dziennego
48. Wymagania normowe oświetlenia dziennego przy projektowaniu budynku
Wykłady z Fizyki Budowli - semestr IV
1. Zakres i znaczenie Fizyki Budowli
Budynki można podzielić na:
- mieszkalne
-użyteczności publicznej
-przemysłowe
-rolnicze
Budynki spełniają różne funkcje. W każdym budynku należy zapewnić warunki eksploatacyjne, odpowiednie funkcje, które wykonuje się w budynku.
Warunki te są:
-temperaturowe
-wilgotnościowe
-akustyczne
-świetlne
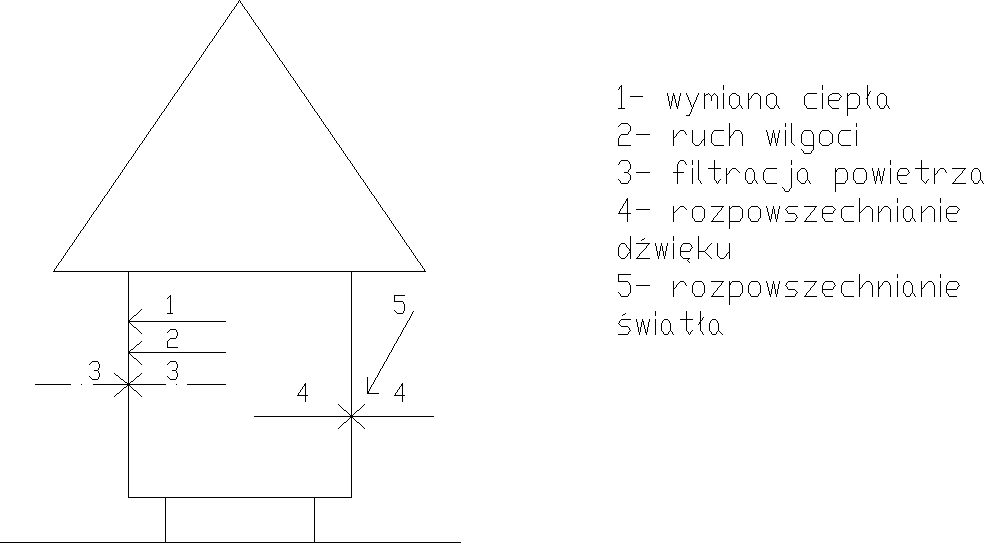
W wyżej wymienione warunki eksploatacyjne w znacznym stopniu zależą od występowania procesów:
-wymiany ciepła
-ruchu wilgoci
-filtracji powierza
-rozpowszechnienia dźwięku
- rozpowszechnienia światła,
które opisuje fizyka budowli

Wymiana ciepła i ruch wilgoci odbywają się przez przegrody budowlane (ściany, okna, drzwi, stropodachy, stropy nad piwnicami). W wyniku różnych temperatur powietrza zewnętrznego i wewnętrznego w okresie zimowym. Ruch wilgoci odbywa się w postaci pary wodnej. Ciepłe powietrz zawiera więcej pary wodnej niż zimne. W związku z tym ciepło i para wodna przemieszcza się w przegrodach od wewnętrznej na zewnętrzną budynku.
Filtracja powietrza odbywa się w wyniku różnic powierza zewnętrznego i wewnętrznego pod wpływem różnicy temperatur oraz ciśnienia wiatru na powierzchni przegród.
W wyniku może być infiltracja (ruch powietrza od zewnątrz do wewnątrz) lub exfiltracja (na odwrót do infiltracji).
Rozpowszechnianie dźwięku to najbardziej skomplikowane zjawisko. Związane to jest z tym, że źródłem dźwięku lub hałasu może być zewnętrze i wewnętrzne. Oprócz tego rozpowszechnianie dźwięku może odbywać się przez powietrze i materiały elementów budynku.
Rozpowszechnianie światła odbywa się przez okna i świetliki. Źródła światła to słońce i sklepienie niebieskie.
Odpowiednio wymienionym zjawiskom fizyka budowli składa się z trzech specjalności naukowych:
- fizyka cieplna (1,2,3 proces)
- akustyka budowlana (4 proces)
- światło dzienne (5 proces)
Wiedzę z fizyki budowli wykorzystuje się do uzasadnienia rozwiązań przestrzennych i konstrukcyjnych budynku. Zasady fizyki budowli wykorzystuje się jako podstawy do pracowania norm projektowania w budownictwie.
2. Formy wymiany ciepła
Ciepło jest jedną z form energii. Jego istota polega na ruchu cząsteczek materii. Wskaźnikiem (miarą) energii jest temperatura ciała. Im jest ona większa tym szybszy jest ruch cząsteczek, czyli wyższy stan energetyczny danego ciała.
Ruch ciepła polega na przekazywaniu energii od ciała o temperaturze wyższej do ciała o temp. niższej.
Wyróżnia się trzy zasadnicze rodzaje wymiany ciepła:
1. przewodzenie ciepła - jest charakterystyczny dla ciał stałych, polega na przenoszeniu energii w wyniku oddziaływań międzycząsteczkowych.
2. konwekcyjny ruch ciepła - ruch ciepła w wyniku przemieszczania się cząsteczek ośrodka; przenoszenie energii odbywa się głównie w wyniku mieszania się cieczy lub gazu (w tych ośrodkach konwekcja ma znaczenie dominujące).
3. przez promieniowanie- odbywa się w gazach lub próżni w wyniku przekazywania energii pomiędzy powierzchniami promieniującymi za pomocą fal elektromagnetycznych.
3. Wymiana ciepła przez konwekcję
Konwencja-zjawisko polegające na zmianie położenia poszczególnych cząsteczek ośrodka. W wyniku różnic gęstości lub wymieszania.
Jeżeli ruch cząstek powietrza lub płynu wywołany jest przez różnicę gęstości, to taką konwencję nazywamy naturalną. W przypadku ruchu spowodowanego działaniem wiatru lub wentylatora, mamy do czynienia z konwencją wymuszoną, która występuje zasadniczo na zewnętrznych powierzchniach budynku.
Konwencyjną wymianę ciepła między powierzchniami przyrody i powietrzem opisuje równanie Newtona:
qk=αk(ti - vi )
qk - gęstość strumienia [W/m2]
αk - współczynnik przejmowania ciepła przez konwekcję [W/m2K]
ti - temperatura ośrodka [K]
vi - temperatura powierzchni [K]
Dla ściany pomieszczenia przy dowolnym przypadku konwekcji:
αk=1,66![]()
Δt - różnica temperatur powierzchni ścianki i powietrza z dala od niej.
Przy konwekcji wymuszonej współczynnik wymiany ciepła na powierzchni zewnętrznej przegród obliczamy:
αk=7,34V0,656+3,78e-1,91V
v - szybkość wiatru [m/s]
e - podstawa logarytmów naturalnych
4. Wymiana ciepła przez promieniowanie
Promieniowanie jest to przenoszenie energii w ośrodku gazowym lub w próżni pomiędzy dwoma promieniującymi powierzchniami za pomocą fal elektromagnetycznych. Przy czym następuje tu dwukrotna zamiana energii:
- cieplnej na elektromagnetyczną; na powierzchni wypromieniowującego ciepło
- elektromagnetycznej na cieplną; na powierzchni ciała pochłaniającego ciepło
Powierzchnie ciał o temperaturze powyżej 00 bezwzględnego są źródłami promieniowania cieplnego o natężeniu zależnym od właściwości i temp. powierzchni. Natężenie ciała absolutnie czarnego E0 określone jest wzorem Stefana-Boltzmanna:
Eo= C0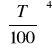
![]()
C0 - współczynnik promieniowania ciała absolutnie czarnego [W/(m2k)]
T - temperatura bezwzględna powierzchni [K]
……….Materiały budowlane, więc powierzchnie przegród są ciałami szarymi. Ciała szare wypromieniowały mniej ciepła, a padający na nie strumień ciepła jest częściowo odbijany, a częściowo pochłaniany.
Stosunek natężenia promieniowania pochłanianego przez powierzchnię ciała szarego do natężenia promieniowania padającego nazywamy współczynnikiem absorpcji ε.
![]()
gdzie:
C - współczynnik promieniowania powierzchni ciała szarego,
ε - współczynnik absorpcji = emisyjności względnej promieniowania powierzchni.
Promieniowanie nie pochłonięte przez powierzchnię materiału nieprzezroczystego ulega odbiciu. Stosunek natężenia promieniowania odbitego do natężenia promieniowania padającego nazywamy współczynnikiem odbicia ρ.
Dla materiałów praktycznie nieprzezroczystych ε+ρ=1, oznacza to, że gdy ciało dobrze pochłonie energię to źle ją odbija i na odwrót.
Współczynnik ε i g zależą od długości fali promieniowania, temperatury ciała i kąta padania promieniowania na daną powierzchnię.
Wszystkie powierzchnie przegród w pomieszczeniach jednocześnie oddają, przyjmują i odbijają ciepło przez promieniowanie. W praktyce rozpatruje się tylko pierwszy etap tego zjawiska.
Strumień ciepła Φ1-2 wymieniany przez promieniowanie z powierzchni F1 do powierzchni F2 wyraża się wzorem:
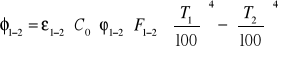
gdzie:
ε1-2 - emisyjność zastępcza dla powierzchni małych lub będących w dużej odległości ciał ε1-2 = ε1 ⋅ε2;
ε1 - współczynnik emisyjności dla powierzchni F1;
ε2 - współczynnik emisyjności dla powierzchni F2.
Dla dwóch powierzchni równoległych mało odległych od siebie:
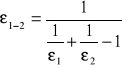
Dla powierzchni F1 całkowicie otaczającej powierzchni F2
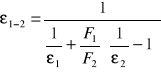
ϕ1-2 - współczynnik konfiguracji lub kątowy współczynnik promieniowania, który określa część całego strumienia ciepła padającego na powierzchnię F2 z powierzchni F1. Przy wymianie ciepła między dwiema nieograniczonymi płaszczyznami ϕ1-2 = 1.
Współczynnik przyjmowania ciepła przez promieniowanie αr wyraża się wzorem:
![]()
5. Złożona wymiana ciepła
Na powierzchni przegród budowlanych występuje jednoczesna wymiana ciepła przez konwekcję i promieniowanie. Zakładamy że gęstość promienia cieplnego g na rozpatrywanej powierzchni jest równa sumie gęstości strumieni cieplnych przekazywanych przez konwekcję qk i promieniowanie qr.
q = qk + qr
W przypadku pomieszczenia z jedną przegrodą zewnętrzną i przy jednakowej emisyjności i temperaturze wszystkich powierzchni możemy zapisać:
q=∝k(ti-vi)+ ∝r(ti-vi)
W przybliżeniu:
q=(∝k+ ∝r)(ti-vi)= ∝i(ti-vi)
gdzie:
αi - współczynnik przyjmowania ciepła przez konwekcję i promieniowanie w powierzchni wewnętrznej przegrody.
Współczynnik αi zależy głównie od różnicy ti-vi oraz od współczynnika promieniowania tej powierzchni.
Podobnie temu odnośnie powierzchni zewnętrznej przegrody możemy zapisać, że:
q=αe(ve-te)
gdzie:
αe - współczynnik oddawania ciepła przez zewnętrzną powierzchnię przegrody
ve - temperatura powierzchni zewnętrznej przegrody
te - temperatura powietrza zewnętrznego.
Współczynnik αe przez zewnętrzną powierzchnię przegrody zależy głównie od prędkości wiatru.
Współczynniki αi, αe mają znaczenie praktyczne przy obliczaniu zapotrzebowania na ciepło pomieszczeń ogrzewanych. Wartości αi, αe dla najczęściej spotykanych przypadków obliczania się z normy cieplnej. Dla ścian zewnętrznych αi = 8,1 W/m2∙K, gdy αe=20 W/ m2∙K. Opór przyjmowany ciepła od strony wewnętrznej równe jest 0,123
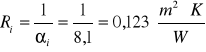
Opór cieplny oddawania ciepła:
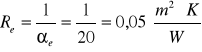
6. Ruch ciepła przez przewodzenie
Wymiana ciepła przez przewodzenie jest charakterystyczna dla ciał stałych.
Rozwiązanie problemu przewodzenia ciepła na jakimś obszarze polega na wyznaczeniu temperatury w dowolnym punkcie tego obszaru i w dowolnej chwili:
t = f(x, y, z, τ)
gdzie:
t - temperatura
x, y, z - współrzędne
τ - czas
Przy stałej temperaturze w czasie (stan ustalony) t = f(x, y, z).
W przypadku jednowymiarowego pole temperatur to jest, gdy temperatura zmienna jest tylko w jednym kierunku, wtedy t = f(x).
W takich warunkach przewodzenie ciepła w ciałach stałych opisuje w sposób ilościowy prawo Fouriera:
![]()
gdzie:
q - wektor gęstość strumienia ciepła
![]()
-spadek temperatury w kierunku współrzędnej x
λ - współczynnik przewodzenia ciepła materiału ośrodka.
Rozwiązanie równania wymaga określenia warunków geometrycznych i podania warunków brzegowych i warunku początkowego.
Przez warunek początkowy rozumie się podanie rozkładu temperatur w rozpatrywanym obszarze w chwili τ=0, wtedy τ (x, y, z, 0) = f(x, y, z).
Warunki brzegowe opisują sposób wymiany ciepła na granicy obszaru o jednorodnych cechach cieplnych, w których przewodzenie ciepła jest opisane jednym równaniem. Najczęściej wyróżnia się następujące przypadki warunków brzegowych:
- warunek I rodzaju, gdy znany jest rozkład temperatur na brzegu obszaru w dowolnej chwili tF(τ) = f(τ)
- warunek II rodzaju, gdy znany jest rozkład gęstości strumienia cieplnego na brzegu obszaru w dowolnej chwili
qF(τ) = q(τ)
- warunek III rodzaju, gdy wymiana ciepła między powierzchnią odbywa się zgodnie z prawem Newtona:
-λ(grad t)F = α(tF - t0)
- warunek IV rodzaju, obejmujący warunki ciągłości temperatury i gęstości strumienia cieplnego na brzegu wspólnym dla obu obszarów.
W fizyce budowli najczęściej spotyka się warunki brzegowe III i IV rodzaju.
![]()
7. Definicja przewodności cieplnej
Przewodność cieplna jest jedną z podstawowych własności decydujących o przydatności danego materiału budowlanego do zastosowania w przegrodach zewnętrznych budynku.
Zdolność przewodzenia ciepła przez materiały budowlane określa współ. Przewodności cieplnej λ [W/(m⋅k)], który można zdefiniować jako gęstość ustalonego strumienia ciepła przepływającego przez jednolitą warstwę materiału, jeżeli spadek temperatury Δt w stosunku do grubości d wynosi 1K/1m
![]()
Przy badaniach laboratoryjnych w warunkach ustalonych dla próbki materiału współczynnik przewodzenia ciepła możemy obliczyć z zależności:
![]()
gdzie:
Q - ilość ciepła [J],
d - grubość przegrody jednolitej [m],
Δt - różnica temperatur na przeciwległych powierzchniach [K],
A - powierzchnia przegrody [m2],
τ - czas przepływu ciepła [s].
Przewodność cieplna materiałów budowlanych zależy od wielu czynników, między innymi od gęstości objętościowej, struktury, wilgotności i temperatury materiału.
8. Zależność współczynnika przewodzenia ciepła od gęstości objętościowej
i struktury materiału
Wraz ze wzrostem gęstości objętościowej rośnie również przewodność cieplna materiałów budowlanych. Dla materiałow lekkich w gęstości objętościowej ![]()
ρ = 20÷100 [kg/m3] (styropian, wełna mineralna, pianka poliuretanowa) λ = 0,03÷0,05 [W/m⋅k]
Dla materiałow kamiennych ρ = 2800 [kg/m3] (granit, marmur) λ = 3,5 [W/m⋅k].
Dla stali budowlanej ρ = 7800 [kg/m3], λ = 5,8 [W/m⋅k].
W materiałach o tej samej substancji stałej, ale różnej gęstości występuje również zróżnicowanie wielkości współczynnika przewodzenia ciepła (λ):
Beton zwykły o ![]()
ρ = 1900 λ = 1,0
Beton zwykły o ![]()
ρ = 2400 λ = 1,5
W materiałach anizotropowych znaczne zróżnicowanie wartości współ. λ występuje w zależności od kierunku przepływu ciepła. Przekładem jest drewno sosnowe ![]()
ρ = 550 [kg/m3 ]. Jeżeli kierunek przepływu ciepła jest wzdłuż włókien λ = 0,30 [W/mK], a jeżeli w poprzek włókien λ = 0,16 [w/mK]. Związane to z tym, że w materiałach o strukturze kapilarno-porowatej, ziarnistej, mieszanej lub włóknistej zachodzi założona wymiana ciepła. Ona odbywa się przez przewodzenie substancji stałej oraz przez przenikanie, promieniowanie i konwekcję w porach materiałów wypełnionych powietrzem. Ponieważ λ powietrza jest znacznie mniejszy (λ pow.=0,024- 0,30 W/mK) od współczynnika λ szkieletu materiału, to wraz ze zmniejszeniem gęstości materiału i tym samym wzrostem porowatości maleje też jego przewodność cieplna.
Jeżeli pory są otwarte lub bardzo duże to w materiale może intensyfikować się ruch powietrza i stąd zwiększa się λ.
9. Zależności współczynnika λ od zawartości wilgoci
Stopień zawilgocenia materiałów budowlanych jest podstawowym czynnikiem wpływającym na wzrost współczynnika przewodzenia ciepła λ. Ze wzrostem wilgotności materiałów wzrastają wartości współczynnika przewodzenia λ.
Przy niewielkich wilgotnościach materiałów i normalnej temperaturze pomiędzy stykającymi się ziarnami materiału błonki wody tworzą tak zwane mostki wodne, które zwiększają powierzchnię kontaktu ziaren przyczyniając się do wzmożonej wymiany ciepła między nimi i do szybkiego wzrostu λ.
λ., [W/mK]
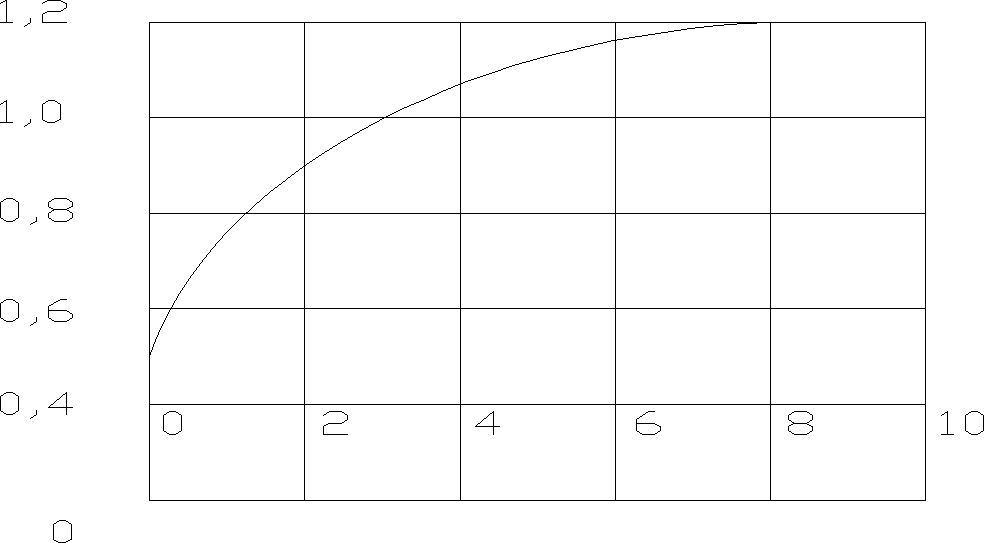
U[%]
Rys. λ cegły ceramicznej w zależności od wilgotności U%

Przy średniej i dużej wilgotności zwiększenie λ związane jest:
z wypieraniem powietrza wypełnianej pory przez wodę, która charakteryzuje się dużo większymi wartościami λ (λw = 0,56 W/mK)
dyfuzją pary wodnej, z którą połączone jest przenoszenie ciepła oraz kapilarne przemieszczanie się wilgoci.
Przy wysokich temperaturach λ z powiększeniem się wilgoci wzrasta szybciej.
Związane to jest z intensywnością dyfuzji pary wodnej.
Przy temp. ujemnych wzrost wilgotności przy niezmienności w pozostałych warunkach również powoduje wzrost λ, ponieważ lód λl = 2,3 W/mK tj. około 4 razy więcej niż woda i około 80 razy więcej niż powietrze w porach. Wzrost ten nie występuje zawsze i nie we wszystkich mat. przykładem tego może być zależność dla cegły piano-silikatowej.
λ, [W/mk]
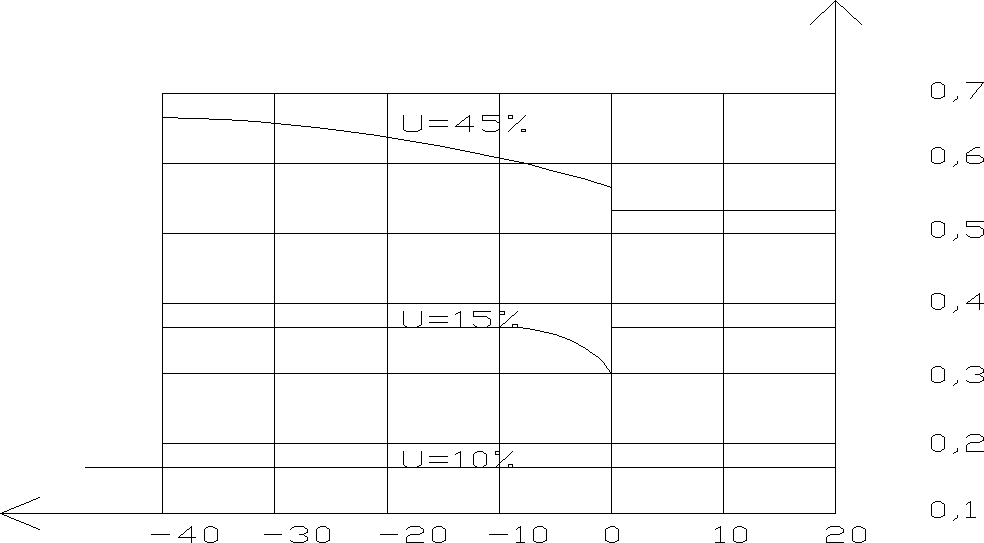
t [0C]
Rys. zależności λ piano-silikatowej ρ = 700 kg/m3od temp. i wilgotności
Charakter tej zależności można objaśnić:
przechodzenie wody w szron, który ma mniejsza przewodność cieplna niż woda
zmniejszenie dyfuzji pary wodnej po zmianie wody w lód
faktem, że woda w porach zamarza nie w temperaturze 0 0C, ale w temperaturze niższej i zależnej od średnicy porów: ![]()
woda zamarza przy -6,4 0C
![]()
przy -14,2 0C
![]()
przy -18,6 0C
10. Wpływ temp na wartość współczynnika λ
Przy wzroście średnicy temp. przewodność cieplna materiałach porowatych, ziarnistych i włóknistych w stanie suchym rośnie. Dzieje się to w wyniku zwiększenie przewodności cieplnej substancji stałej, a także powietrza zawartego w porach oraz zwiększenie się wymiany ciepła przez promieniowanie i w nie wielkim stopniu przez konwekcję.
Wpływ temperatury na przewodność cieplną materiału opisuje wzór:
λt = λ0(1+β⋅t)
gdzie:
λt - współczynnik przewodności cieplnej materiału t [°C]
λ0 - współczynnik przewodności cieplnej materiału t = 0°C
t - temperatura materiału
β - współczynnik temperatur ≈ 0,0025
Wzrost przewodności cieplnej wraz z temperaturą jest stosunkowo niewielki i ma praktycznie znaczenie dla materiałów zastosowanych w wysokich temperaturach (powyżej 500°C). W przegrodach budowlanych pracujących w t = (-40÷60°C) zmiany przewodności są stosunkowo małe i dlatego zwykle są pomijane.
11. Obliczeniowe wartości współczynnika λ
Przewodność cieplna materiałów zawilgoconych jest znacznie większa od przewodzenia tych materiałów w stanie suchym. W związku z tym bardzo istotne są warunki w budowaniu i eksploatacji materiałów przegród budowlanych.
Stan wilgotnościowy przegród budowlanych można podzielić na dwa okresy:
1) - początkowy, trwający przez pierwsze lata użytkowania budynku po jego
zasiedleniu (1-3 lat)
2) - eksploatacyjny, odpowiadający długiemu okresowi eksploatacji obiektu.
W początkowym okresie odbywa się obsychanie przegród z wilgoci budowlanej powstającej w wyniku mokrych procesów technologicznych oraz zawilgocenia materiałów w czasie transportu i składowania. Proces ten w zależności od konstrukcji ścian, może trwać od kilku miesięcy do kilku lat.
W okresie eksploatacji budynku wilgotność mat. w przegrodach stabilizuje się na poziomie stanu równowagi względem oddziałującego na przegrodę środowiska zewnętrznego i wewnętrznego. Przy tym wilgotność przegrody zmienia się okresowo w ciągu roku wokół jej średniej wartości w marcu, w kwietniu ona wzrasta, w październiku obniża się, w styczniu zbliża się ona do średnich rocznych wartości.
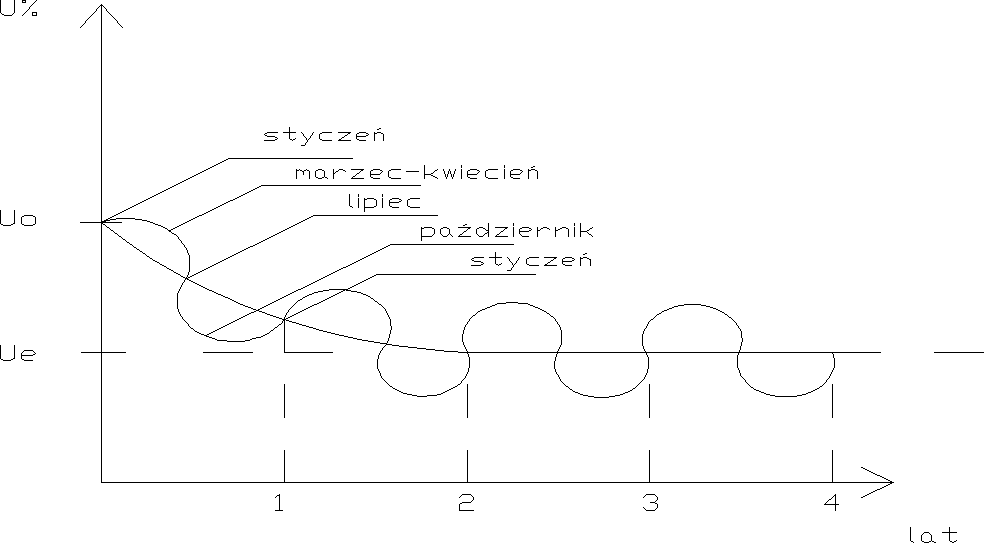
Obliczenia cieplne przegród wykonywane są dla najchłodniejszego okresu zimna, który zazwyczaj jest w styczniu. Dlatego fizyczne wielkości λ, zależne od wilgotności, przyjmuje się dla średniej rocznej wilgotności materiału w przegrodzie.
Uwzględniając zawilgocenie materiałów dokonuje się przez przyjęcie jednej z dwóch wartości liczbowych λ podanych w załączniku 4 normy „Cieplnej ochrony budynku”. Przy tym pomieszczenia o wilgotności względnej powietrza w okresie zimowym:
![]()
, λ z kolumny 5
![]()
, λ z kolumny 4
W związku z dużą liczbą produkcji materiałów ociepleniowych i koniecznością podwyższenia jakości mat. ociepleniowych w ostatnich czasach wprowadzono pojęcie deklarowanej wartości współczynnika przewodzenia ciepła. Proponuje się, że dostawca partii materiału gwarantuje, że przy poziomie ufności p=90 (90% materiałów będzie posiadać wartość współczynnika nie mniej niż zadeklarowano).
Wartość deklarowana to wartość statystyczna oczekiwana zaokrąglona według zasad:
- dla λ![]()
0,08 - zaokrąglenie z nadmiarem do 0,001 [W/mK]
- dla 0,08<λ![]()
0,2 - zaokrąglenie z nadmiarem do 0,005 [W/mK]
- dla 0,2<λ![]()
2,0 - zaokrąglenie z nadmiarem do 0,01 [W/mK]
- dla λ>2,0 - zaokrąglenie z nadmiarem do 0,1 [W/mK]
12. Jednowymiarowe ustalone przewodzenie ciepła
Z prawa Furiera :
![]()
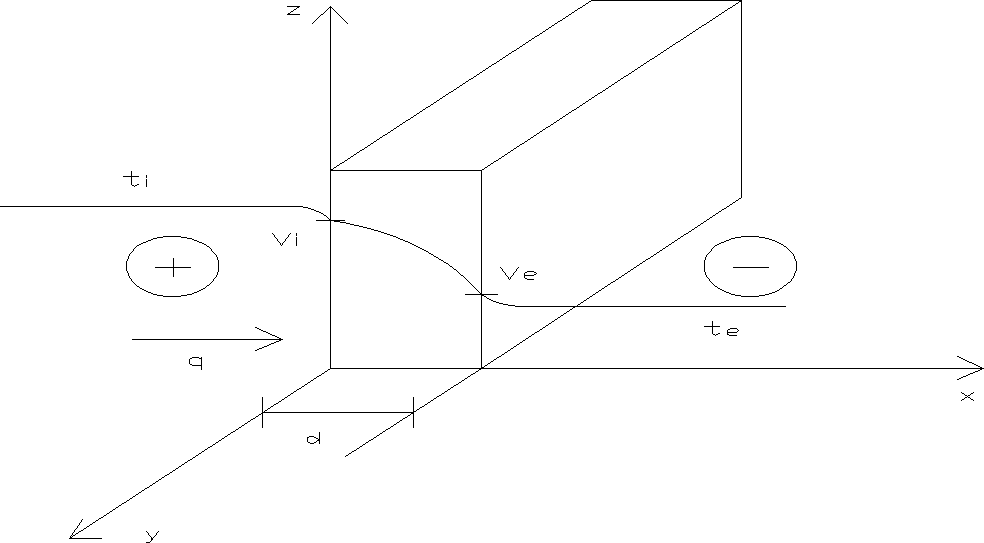
wynika, że w najprostszym przypadku ustalonego przewodzenia ciepła przy jednokierunkowym przepływie w jedno materiałowej ściance płaskiej grubości d oraz oznaczonych warunkach brzegowych trzeciego rodzaju gęstość strumienia cieplnego można obliczyć ze wzoru:
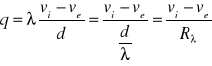
Przy znanych temperaturach powietrza wewnętrznego (ti) i zewnętrznego (te)
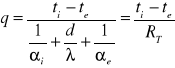
gdzie:
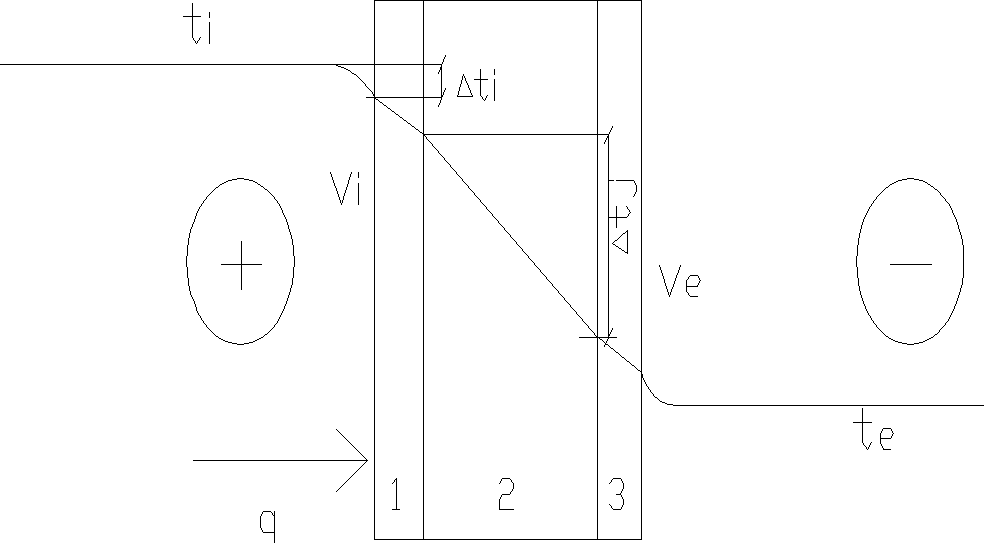
Vi, Ve - temp. wewnętrzna i zewnętrzna powierzchni ściany
ti, te - temp. powietrza wewnętrzna i zewnętrzna
αi, αe - współ. przejmowania ciepła, odpowiednio od strony wewnętrznej i zewnętrznej przegrody
d - grubość ścianki
λ - współczynnik przewodzenia ciepła
![]()
- opór cieplny ścianki
![]()
- całkowity opór cieplny ścianki
Dla przegrody wielowarstwowej ze szczelinami powietrznymi całkowity opór
cieplny RW oblicza się ze wzoru:
![]()
gdzie:
di - grubość i-tej warstwy ścianki
λi - współczynnik przewodzenia ciepła materiału i-tej warstwy
Rpj - opór cieplny i-tej szczeliny powietrznej
Najczęściej posługujemy się odwrotnością oporu cieplnego, która nazywa się
współczynnikiem przenikania ciepła U [W/m2K]. Dla ścianki jednowarstwowej:
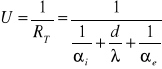
Dla ścianki n- warstwowej z m- pustkami powietrznymi:
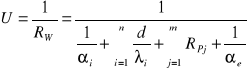
Współczynnik U ma podstawowe znaczenie w praktyce budowlanej, gdyż w normie
cieplnej podano jego maksymalne wartości, które uwzględniamy w obliczeniach praktycznych.
Stosując współczynnik U przegrody gęstość strumienia ciepła q można wyrazić
wzorem:
q = U (ti - te)
Rozpatrując przepływ ciepła przez pow. wewnętrzną przegrody wielkość q
wyrażamy wzorem:
![]()
Dla każdej z warstw przegrody :
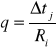
gdzie :
Δtj - różnica wartości temp. pomieszczeń ograniczonych j - tą warstwą
Rj - opór cieplny j - tej warstwy
Wtedy różnica temp. na powierzchni wewnętrznej przegrody :
![]()
Różnica temp. na powierzchni j - tej warstwy :
![]()
a na powierzchni przegrody wielowarstwowej :
![]()
W takim razie temperatura na pow. przegrody od strony napływu ciepła można
wyrazić wzorem:
![]()
a temp. na styku n - tej i n+1 warstwy
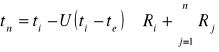
Warstwy temp. t n i Vi mają ważne znaczenie przy ocenie stanu wilgotności przegród.
Dwukierunkowy przepływ ciepła
W przegrodach o konstrukcji niejednorodnej a więc wykonanych z różnych mat. i o konfiguracji zachodzi konieczność określenia pola temperatury przy dwukierunkowym przepływie ciepła.
Znalezienie pola temperatury w płaskim układzie współrzędnych polega na rozwiązaniu równania Laplace'a
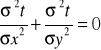
gdzie:
t - temperatura w dowolnym punkcie układu
x, y - współrzędne punktu
Często stosowane są metody rozwiązywania równań Laplace'a. Jedną z nich jest metoda różnic skończonych.
Na obszary, których chcemy określić pole temperatur nakłada się siatkę kwadratów, siatkę dobieramy tak, aby węzły jej leżały wewnątrz i na brzegu rozpatrywanego obszaru oraz w charakterystycznych punktach.
Równanie ustalonego przewodzenia ciepła dla takiej siatki posługując się różnicami skończonymi należy zapisać w postaci:
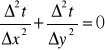
Rozwiązując równania w odniesieniu do temperatury 0 w dowolnym węźle siatki dla konstrukcji jednorodnej można przedstawić w postaci:
![]()
Dla konstrukcji niejednorodnych jest przy zastosowaniu siatki o dowolnej podziałce rozwiązanie równania różnic skończonych względem toru ma postać:
![]()
gdzie:
U0-1, U0-2, U0-3, U0-4 - wskaźniki przewodności połączeń siatki cieplnej między odpowiednimi węzłami.
![]()
Ri - j - opis cieplny między węzłami i -j
Dla jednakowych objętości elementu:
![]()
l - długość elementu wieńca w kierunku w którym wyznaczany jest opór cieplny
F - pole przekroju elementu prostopadłego do tego kierunku
Opór wymiany ciepła na powierzchni graniczącej z powietrzem wynosi:
![]()
![]()
- wsp przejmowania ciepła na tej powierzchni
F- pole powierzchni elementu
Określenie oporów siatki na granicy ciała i środowiska otaczającego wykonuje się w następujący sposób:
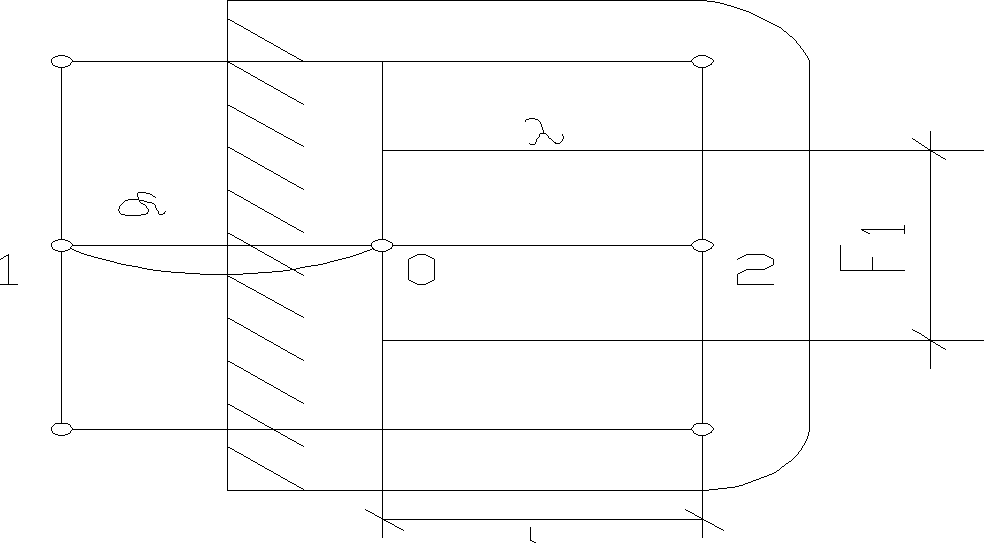
![]()
; ![]()
; ![]()
; ![]()
Obliczanie siatki sprowadza się do rozwiązania układów równań liniowych składających się z tylu równań, ile jest węzłów w przyjętej siatce cieplnej. Metodę siatki można stosować praktycznie we wszystkich przypadkach dowolnie złożonych z wewnętrznymi źródłami lub stratami ciepła itp.
Obliczanie pól temperatur metodą siatek jest pracochłonne i wymaga wykorzystania programów komputerowych.
14. Obliczania przenikania ciepła przez przegrody zewnętrzne budynku.
Współczynnik przenikania ciepła dla przegród jednolitych oblicza się ze wzoru:
![]()
gdzie:
Ri, Re - opory przejmowania ciepła odpowiednio po stronie wewnętrznej i zewnętrznej
przegrody [(m2 K)/W]]
R - opór cieplny przegrody.
![]()
![]()
gdzie:
![]()
- współczynnik przenikania ciepła od wewnątrz
![]()
- współczynnik przejmowania ciepła od zewnątrz
Oprócz przegród jednolitych istnieją przegrody niejednolite ( to ściany z pustaków, ściany i stropy złożone z warstw jednolitych, ściany z cegły i betonu komórkowego, w którym są słupy wieńce i nadproża żelbetowe lub przez które przenikają przegrody wewnętrzne wykonane z betonu i żelbetu).
W przegrodzie o konstrukcji niejednolitej, której stosunek największego do najmniejszego miejscowego oporu cieplnego nie jest większy od 5, średni współczynnik przenikania ciepła:
![]()
![]()
gdzie:
U1, U2, ...,Un - współczynniki przenikania ciepła poszczególnych wycinków przegrody
A1, A2, ...An - powierzchnia wycinków przegrody uzyskany przez umowny podział tej
Przegrody
A = A1 + A2 + ... + An
A - całkowita powierzchnia przegrody
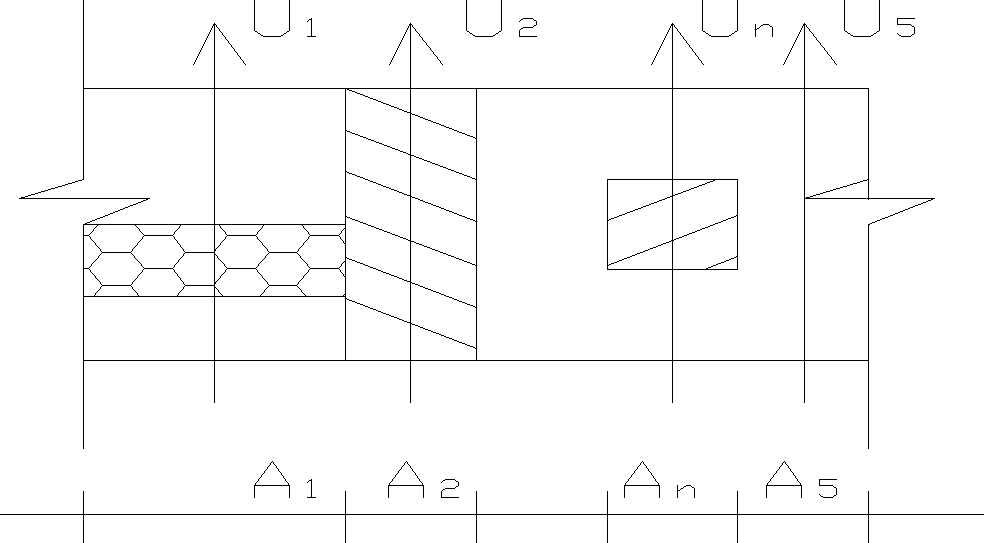
Fragmenty przegród niejednolitych wykonane z materiałów o większych wartościach λ niż pozostała część konstrukcji nazywają się mostkami termicznymi. W miejscach mostków termicznych występuje zwiększony przepływ ciepła, a na ich wewnętrznej powierzchni utrzymuje się niższa temperatura w porównaniu z temperaturą w pozostałej części przegrody.
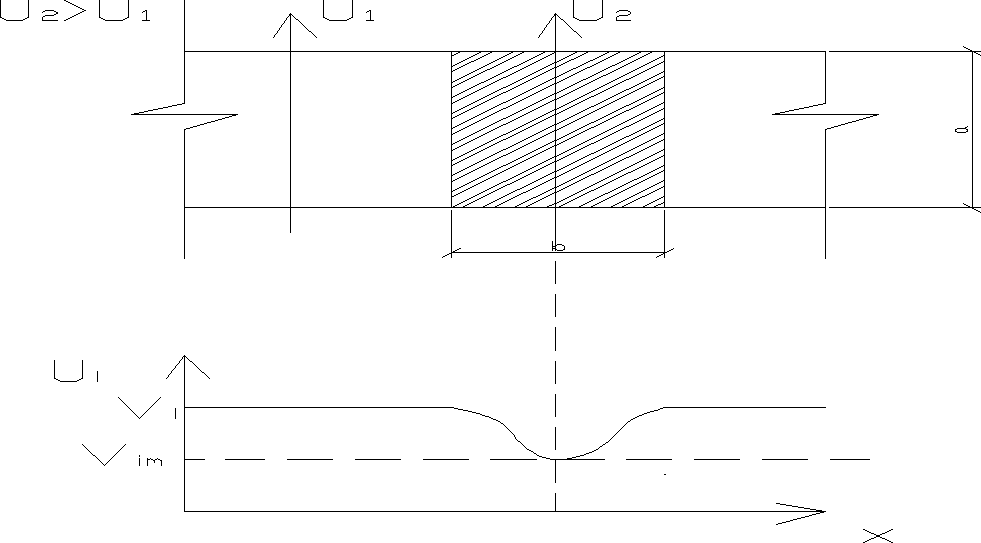
Dla mostka termicznego utworzonego z materiałów o λ≤1,7[W/mK]. Temperatura dla wewnętrznej powierzchni można obliczyć ze wzorów:
a) przy stosunku b/a > 1,5
Vim = ti - Um(ti - te)Ri
b) przy stosunku b/a ≤ 1,5
Vim = ti -[U + η(Um - U)](ti - te)Ri
gdzie:
Um - współczynnik przenikania ciepła w miejscu mostka termicznego [W/m2k]
η - współczynnik poprawkowy przyjmowany z tabeli gdzie η = f(b/a)
Współczynnik przenikania ciepła „U” dla przegród, w których występują mostki termiczne liniowe i punktowe można wyznaczyć ze wzoru:
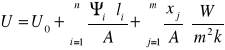
gdzie:
U0 - współczynnik przenikania ciepła bez uwzględnienia wpływu mostka,
![]()
i - liniowy współczynnik przenikania ciepła dla mostka liniowego o numerze i,
li - długość mostka termicznego o numerze i,
Xj - punktowy współczynnik przenikania ciepła dla mostka punktowego o numerze j,
A - pole powierzchni przegrody
Współ. ![]()
i Xj należy określić eksperymentalnie lub obliczyć za pomocą programów komputerowych.
Dla części stosowanych przypadków w budownictwie te wartości można znaleźć w literaturze.
Współczynnik U dla przegrody z mostkami termicznymi (okna, drzwi i inne) można obliczyć w sposób uproszczony. W budynkach o ogrzewanej kubaturze ≤1500m3, współczynnik U można wrazić wzorem:
U = U0 + ΔU [W/m2K]
gdzie:
ΔU - dodatek do współczynnika U0 uwzględniający wpływ mostków termicznych (przyjmuje się z tabeli ΔU=f(rodzaj mostka); ΔU=0,1÷0,25
- dla ścian zewnętrznych z oknem ΔU=0,15
- dla ściany zewnętrznej z oknem + drzwi balkonowe ΔU=0,20)
Współczynnik przenikania ciepła dla ścian przyległych do gruntu:
![]()
gdzie:
R- opór cieplny przegrody
Ru - opór obliczeniowy gruntu [ m2k/W]
Opór cieplny gruntu uzależniony jest od odległości H mierzonej od górnej powierzchni podłogi do powierzchni terenu.
15. Opór cieplny przegród ze szczelinami
Suche powietrze w bezruchu ma mały współczynnik przewodności cieplnej (λp = 0,024 W/m2k). W zamkniętych szczelinach powietrznych przewodność cieplna powietrza znacznie się zwiększa. Spowodowane jest to głównie konwekcją, to jest ruchem powietrza, który występuje na skutek ogrzewania się powietrza na cieplejszej powierzchni i ochładzania się na powierzchni zimniejszej.
W mniejszym stopniu wymiana ciepła występuje przez promieniowanie, na skutek różnicy temperatur na powierzchniach pustki powietrza. Przewodzenie ciepła ma najmniejszy udział.
Ze wzrostem temperatury i grubości szczeliny pionowej wymiana ciepła przez konwekcję zwiększa się. W szczelinach poziomych przy przepływie ciepła z dołu do góry, wymiana ciepła wzrasta, a przy przepływie z góry do dołu wymiana ciepła przez konwekcję nie występuje.
Opór cieplny pustki powietrznej do 3cm rośnie, a dalsze zwiększanie grubości nie daje już przyrostu oporu cieplnego.
Opór cieplny pustki powietrznej zwiększa się przy niższej temperaturze, dlatego szczeliny powietrzne należy stosować bliżej powierzchni zewnętrznej przegrody.
Dla praktycznych obliczeń wielkości liczbowe oporów cieplnych, szczelin zamkniętych można przyjmować z normy cieplnej.
Rj= f(d)![]()
W celu zmniejszenia skraplania się pary wodnej na chłodniejszych powierzchniach szczeliny stosuje się wentylacje szczelin powietrznych zewnętrznych. Temperatura powietrza w tej szczelinie jest bliska temperaturze powietrza zewnętrznego i zależy również od grubości szczeliny, jej usytuowania w przegrodzie.
Opór cieplny szczeliny wentylacyjnej oraz warstw przegrody znajdujących się po jej zewnętrznej stronie będzie zróżnicowany.
W ścianach zewnętrznych, gdy wentylowana szczelina powietrzna jest pod okładziną z blachy lub ze szkła, to opór cieplny tej szczeliny, a także okładziny nie powinien być uwzględniony przy obliczaniu całkowitego oporu cieplnego ściany.
16. Obliczanie wartości temperatur ogrzewanych pomieszczeń w
budynkach i powietrza zewnętrznego
Wartość temperatury obliczeniowej powietrza wewnętrznego (ti) przyjmuje się w zależności od sposobu wykorzystania pomieszczeń i w zależności od rodzaju wykonywanych czynności oraz ubioru ludzi. Wartości temperatury obliczeniowej maja zapewnić optymalne warunki do wykonywania pracy lub odpoczynku w pomieszczeniach i powinien być stabilny.
W pomieszczeniach przeznaczonych do stałego przebywania ludzi znajdujących się w okryciach zewnętrznych lub wykonujących pracę fizyczną ti = +12oC.
W pomieszczeniach przeznaczonych do przebywania ludzi w okryciach zewnętrznych w pozycji siedzącej, bez okryć zewnętrznych wykonujących lżejsze prace fizyczne ti = +16oC.
W pomieszczeniach przeznaczonych do przebywania ludzi bez okryć zewnętrznych nie wykonujących w sposób ciągły pracy fizycznej ti = +20oC.
W pomieszczeniach przeznaczonych do rozbierania i przebywania ludzi bez odzieży ti = +25oC.
Temperatura obliczeniowa powietrza zewnętrznego (te) przyjmowana jest jako średnia z trzech najchłodniejszych okresów 5-cio dobowych w styczniu w ciągu 25 lat.
Temperatury te w Polsce zostały zróżnicowane co 20 w zależności od pięciu stref klimatycznych.
- dla I strefy te= -160C
- dla II strefy te= -180C
- dla III strefy te= -200C
- dla IV strefy te= -220C
- dla V strefy te= -240C
Miejscowości znajdujące się na pograniczu stref, których położenie w jednej lub drugiej strefie nie jest wyraźnie ustalone na mapie, należy zaliczyć do strefy z niższą temperaturą.
Antarktyda - 88,30C Meksyk + 57,80C
Rosja - 720C California + 56,70C
Grenlandia - 660C Termez + 500C
17. Wymagania termoizolacyjne dla ścian, stropów i stropodachów
W budynkach mieszkalnych wielorodzinnych średnie straty ciepła przez ściany zewnętrzne wynoszą 34%, przy stropodachu 6%, przy stropie nad piwnicą 2,5%. W budynkach jednorodzinnych odpowiednio 39%, 18% i 11%.
Jednym ze sposobów znacznego zmniejszenia zapotrzebowania na energię do ogrzewania budynków może być zwiększenie izolacyjności cieplnej przegród. Według obecnej normy cieplnej wartości współczynnika przenikania ciepła U dla przegród, obliczone z uwzględnieniem mostków termicznych, nie mogą być większe od maksymalnych wartości Umax = tj U≤Umax
W budynkach mieszkalnych - dla ścian zewnętrznych warstwowych o izolacji z materiału: λ ≤ 0,05 [W/m2K], przy ti < 16oC; Umax = 0,30 [W/m2K]. Dla pozostałych ścian przy temperaturze ti>16 oC Umax = 0,50 [W/m2K].
Przy ti ≤ 16oC, niezależnie od rodzaju ściany Umax = 0,80 [W/m2K]
Dla stropodachów przy ti >16oC, Umax = 0,30 [W/m2K]; przy 8oC<ti≤16oC Umax = 0,50 [W/m2K]
Dla stropów nad piwnicami nie ogrzewanymi Umax = 0,60 [W/m2K]
Dla okien i drzwi blokowych:
- w I, II, III strefie klimatycznej Umax = 2,60 [W/m2K]
- w IV, V strefie klimatycznej Umax = 2,0 [W/m2K]
Dla drzwi zewnętrznych Umax = 3,0 [W/m2k].
Wartość Umax dla budynków użyteczności publicznej i przemysłowej przyjmuje się z normy cieplnej.
W normie cieplej wprowadzono obowiązek ograniczania powierzchni okien. Ich powierzchnia A0 na każdej kondygnacji nie może przekraczać wartości A0max. A0≤ A0max
A0max = 0,15Az + 0,03Aw
gdzie:
Az - pole powierzchni rzutu poziomego danej kondygnacji w pasie szerokości 5 m wzdłuż ścian zewnętrznych,
Aw - pole powierzchni części rzutu po odjęciu Az.
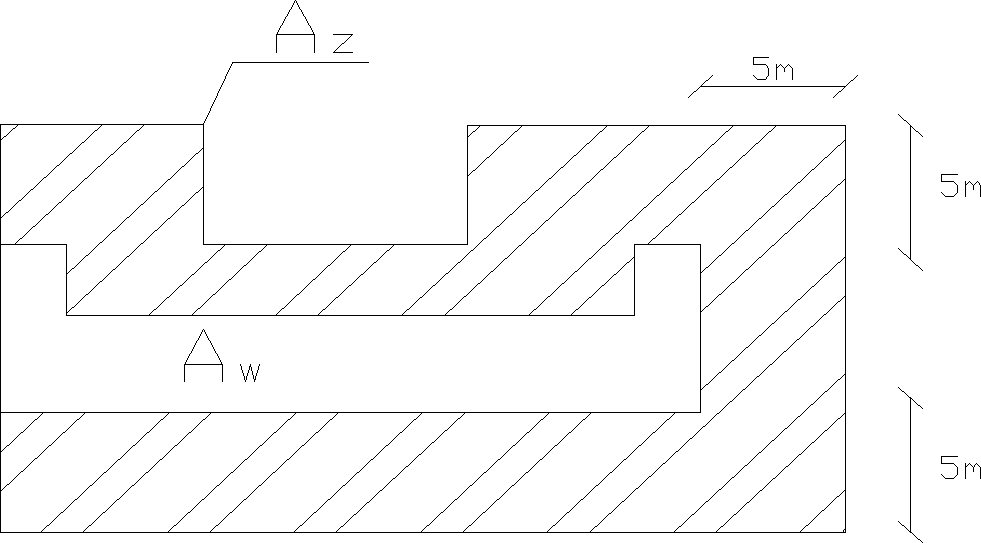
Dla ściany zewnętrznej w pomieszczeniu ogrzewanym stykającym się z gruntem, wartość współczynnika Ug nie powinna być ≤ niż Ugmax
Przy ti≥16 oC ; Ugmax = 1,0[W/m2K]
Przy 40 < ti ≤16 oC ; Ug = 1,25[W/m2K]
Podane wartości Ugmax są wymagane dla ścian na głębokości tylko do 1m poniżej powierzchni terenu.
18. Filtracja powietrza przez przegrody budowlane
Powolny przepływ powietrza przez materiały porowate lub szczeliny pod wpływem różnych ciśnień nazywamy filtracją powietrza. Przepływ powietrza z zewnątrz do pomieszczenia jest infiltracją. Przepływ powietrza z pomieszczenia na zewnątrz jest eksfiltracją.
Infiltracja powietrza zewnętrznego przez przegrody budowlane obywa się
pod wpływem dwóch czynników:
1) różnicy temp., a tym samym różnicy gęstości powietrza
w pomieszczeniu i atmosferycznego,
nadciśnienia wywołanego parciem wiatru na przegrody
zewnętrzne.
Różnicę ciśnień wywołaną różnicą temperatur można obliczyć ze wzoru:
![]()
gdzie:
pe, pi - gęstość powietrza odpowiednio atmosferycznego i w pomieszczeniu,
g - przyśpieszenie ziemskie,
h - odległość między otworami wywiewnymi i osią obojętną [m].
Wartość h przyjmujemy w sposób następujący. W przypadku infiltracji przez szczelinę okna h= połowie wysokości okna. W przypadku istnienia kanałów wentylacji grawitacyjnej, h= od poziomu wylotu komina do poziomu usytuowania kratki wentylacyjnej w pomieszczeniu. W przypadku wymiany powietrza między pomieszczeniem i pozostałą częścią budynku, h = od połowy wysokości budynku do osi okna w danym pomieszczeniu.
Różnice ciśnień między powietrzem w pomieszczeniu i powietrzem atmosferycznym, wywołaną działaniem wiatru określa się ze wzoru:
![]()
gdzie:
C- współczynnik aerodynamiczny,
v - prędkość wiatru,
pe, pi - gęstość powietrza odpowiednio atmosferycznego i w pomieszczeniu.
Sumaryczna różnica ciśnień.
![]()
Ustalono zależność między jednostkowym strumieniem powietrza
i przepływem przez szczeliny w oknach, a różnicą ciśnień
I = a (Δp)n
gdzie:
a- współczynnik infiltracji powietrza przez szczeliny, stolarkę budowlaną [m3/(mhdaPa2/3)]
n- współczynnik potęgowy zmieniający się od 0,5 do 0,8,
Wartość „a” dla gotowych wyrobów nie powinna być większa;
amax = 1,0 [m3/(mhdaPa2/3)] w budynkach powyżej dwóch kondygnacji
amax = 1,8 [m3/(mhdaPa2/3)] w budynkach do dwóch kondygnacji
Całkowity strumień powietrza infiltrowanego v można określić ze wzoru:
v = ![]()
gdzie:
L - długość szczeliny w oknie[m]
Strumień ciepła wymienianego z otoczeniem na skutek infiltracji powietrza można obliczyć ze wzoru:
![]()
gdzie:
Cp - ciepło właściwe powietrza przy stałym ciśnieniu [kJ/(kg*k)]
Przy wystąpieniu dużych wartości ciśnień ilość ciepła potrzebna do ogrzania powietrza infiltrującego może być nawet większa od strat ciepła przez przenikanie.
19. Komfort cieplny pomieszczeń
Przy określaniu warunków panujących w pomieszczeniu używa się pojęć:
-mikroklimat
-komfort cieplny
Przez pojęcie mikroklimatu wnętrz rozumie się zespół parametrów fizycznych i chemicznych pomieszczeń wywierające wpływ na organizm człowieka. Do głównych parametrów mikroklimatu zaliczamy:
1) temperatura powietrza t1
2) średnia temperatura powierzchni przegród tr
3) prędkość ruchu powietrza υ
4) wilgotność powietrza γ
5) zanieczyszczenie powietrza C,[%]
6) jonizacja powietrza,
7) poziom hałasu
8) oświetlenie
Komfort cieplny określa taki stan otoczenia, na którym jest zachowana równowaga cieplna organizmu ludzkiego.
Stopień obciążenia układu termoregulacyjnego organizmu zależy od wymienionych wyżej parametrów mikroklimatu, od rodzaju wykonywanych czynności w pomieszczeniu oraz izolacyjności cieplnej odzieży. Ogólne równanie bilansu cieplnego organizmu wyrażamy wzorem:
S= M -W ± E ± R ± C [W/m2·K]
gdzie:
S - strumień ciepła związany ze wzrostem temperatury ciała człowieka
M - strumień ciepła produkowanego przez organizm w wyniku przemiany materii czy metabolizmu
W- strumień ciepła związany z wykonywaniem pracy zewnętrznej
E- strumień ciepła traconego w wyniku odparowania wody.
R- strumień ciepła traconego przez promieniowanie do otoczenia.
C-strumień ciepła traconego przez konwekcję,
Organizm człowieka może samoczynnie przystosować się tylko w pewnych niewielkich granicach do zmian warunków otoczenia. Przekroczenie tych granic prowadzi do zachwiania równowagi cieplnej organizmu co grozi zdrowiu człowieka. Dlatego w pomieszczeniach przeznaczonych do mieszkania, pracy i wypoczynku należy stwarzać optymalne warunki z zależności od rodzaju ich użytkowania.
W okresie zimowym czynnikiem decydującym o odczuciu komfortu cieplnego, gdy powietrze jest w bezruchu, jest temperatura odczuwalna tm (wyznaczamy ze wzoru):
![]()
Gdy powietrze jest w ruchu to przy wysokich temperaturach pomieszczenia dla określonych temperatur i prężności pary wodnej istnieją optymalne prędkości powietrza odpowiadające warunkom komfortu cieplnego.
Warunki optymalne do pracy o średnim stopniu uciążliwości wykonywane w lekkiej odzieży można przedstawić w sposób graficzny:
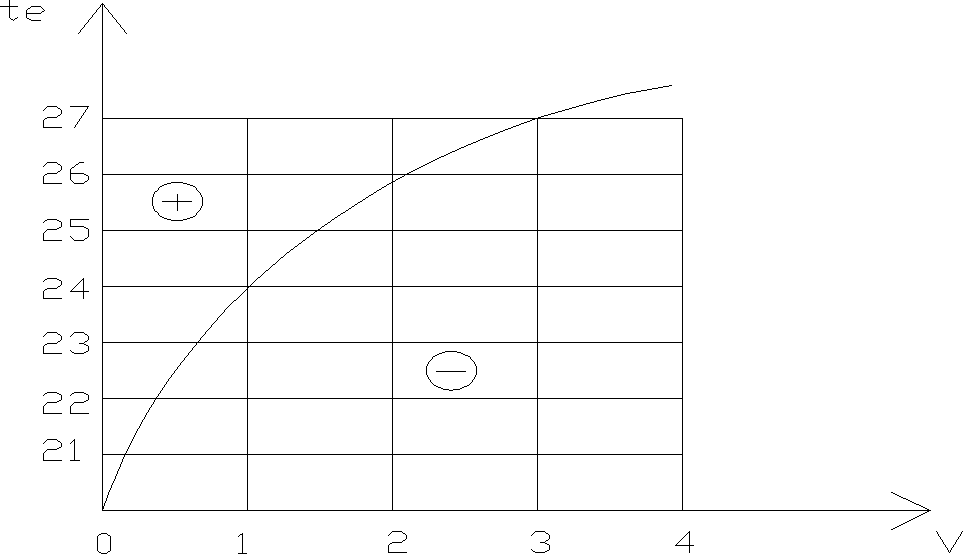
Przy temperaturze powietrza < 9 ºC ruch powietrza zawsze powoduje odbieganie od warunków komfortu nawet dla pracy ciężkiej. Dla odczucia komfortu istotne jest przyzwyczajenie ludzi.
Za najwłaściwszy poziom temperatury odczuwalnej w okresie zimowym przyjmuje się:
+ 20 ºC - w pomieszczeniach mieszkalnych oraz przeznaczonych na pracę
umysłową
+ 12 ºC - 16 ºC - w pomieszczeniach w których wykonuje się pracę fizyczną ( w
zależności od intensywności pracy).
Wilgotność powietrza przyjmuje się w granicach od 30 do 60% (50% wilgotność idealna).
Prędkość ruchu powietrza - poniżej 0,2 m/s
W okresie letnim parametry mikro klimatu nie normują się. Obecnie w Polsce komfort cieplny określa się za pomocą metody Faugera, która przewiduje określenie wskaźników PMV i PPD. PMV - to przewidywana średnia ocena. PPD - to przewidywany odsetek niezadowolonych.
PMV - to wskaźnik, który przewiduje średnią ocenę dużej grupy osób określających swe wrażenia cieplne w siedmio - stopniowej skali ocen:
+ 3 - gorąco
+ 2 - ciepło
+ 1 - dość ciepło
0 - obojętnie
-1 - dość chłodno
- 2 - chłodno
- 3 - zimno
PMV zależy w sposób skomplikowany od parametrów:
1) metabolizmu M
2) pracy zewnętrznej W
3) oporu cieplnego odzieży Jcl
4) stosunku pół powierzchni. ciała okrytego odzieżą do pola powierzchni
ciała okrytego fcl
5) temperatury powietrza ti
6) temperatury promieniowania czy temp. pow. otaczającej tr
7) prędkość przepływu powietrza υ
8) ciśnienia cząstkowego pary wodnej Pa
9) współczynnika wymiany ciepła przez konwekcję hc
10) temperatury powierzchni odzieży tcl
Wskaźnik PPD stanowi prognozę liczby osób odczuwających brak komfortu cieplnego. Jest związany ze wskaźnikiem PMV
Zależność PPD od PMV w postaci graficznej jest następująca:
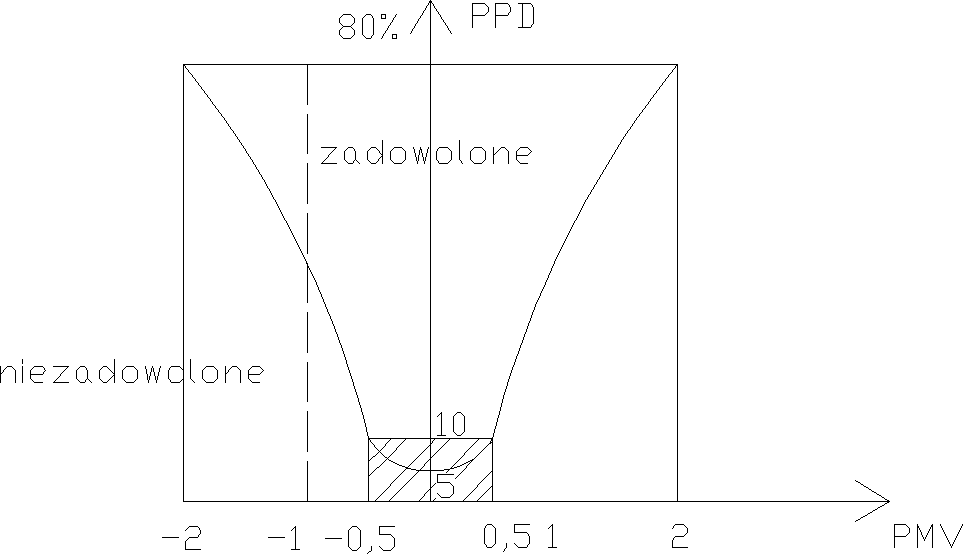
Stosowanie wskaźnika zaleca się tylko dla wartości zawartych w granicach od -2 do +2 , ale komfort cieplny będzie zapewniony gdy PMV (-0,5 do +0,5). Odpowiada to 10% wskaźnikowi PPD.
20.Zasady obliczania sezonowego zapotrzebowania na ciepło do
ogrzewania budynków
Zasady obliczania sezonowego zapotrzebowania na ciepło podano zgodnie z
Literaturą: [5] Instrukcja nr 342/96.Uproszczony sposób obliczania sezonowego
Zapotrzebowania na ciepło do ogrzewania budynków mieszkalnych.
ITB; W-wa 1996r.
Sezonowe zapotrzebowanie na ciepło do ogrzewania budynków oblicza się
jako różnice strat ciepła (przez przenikanie i na podgrzanie powierzchni wentyla.)
i wykorzystywanych zysków ciepła(od promienia słonecznego i źródeł wewnętrznych)
Sezonowe zapotrzebowanie na ciepło Qn [kWh/rok] obliczamy:
Qn = Q2 + Q0 + Qd + Qsp + Qg + Qv - ηc( Qs + Qi)
gdzie:
Q2 - straty ciepła przez przenikanie przez ściany zewnętrzne
Q0 - straty ciepła przez przenikanie przez okna
Qd - straty ciepła przez przenikanie przez stropodachy,
Qsp - straty ciepła przez przenikanie przez strop nad piwnicą nie ogrzewaną
Qg - straty ciepła przez przenikanie do gruntu,
Qv - straty ciepła na podgrzanie powietrza wentylacyjnego,
Qs - zyski ciepła od słońca,
Qi - wewnętrzne zyski ciepła
ηc - współczynnik wykorzystania zysków ciepła,
![]()
gdzie:
GLRc - iloraz sumy zysków ciepła i sumy strat w całym sezonie ogrzewczym
![]()
Wskaźnik sezonowego zapotrzebowania na ciepło do ogrzewania budynku E [kWh/(m3rok)] oblicza się ze wzoru:
![]()
gdzie:
v- kubatura ogrzewania budynku [m3]
Dla budynku mieszkalnego w zabudowie jednorodzinnej oraz dla budynku użyteczności publicznej i budynku przemysłowego wymagania uznaje się za spełnione, jeżeli wartość wskaźnika E jest mniejsza od wartości granicznej E0
E < E0
Dla budynku mieszkalnego w zabudowie jednorodzinnej oraz dla budynku użyteczności publicznej i budynkach przemysłowych wymagania uznaje się za
Spełnione, jeżeli :
E < E0 lub U<Umax
Wartości graniczne E0 zależą od stosunku A/V
gdzie:
A-suma pól powierzchni wszystkich ścian zewnętrznych, dachów, stropodachów,
podłóg na gruncie lub stropów nad piwnicą nie ogrzewaną.
Dla budynków mieszkalnych i zamieszkania zbiorowego przy:
- A/V ≤ 0,20 ; E0 = 29 [kWh/(m3rok)]
-0,20 < A/V ≤ 0,90; E0 = 26,6 + 12A/V[kWh/(m3rok)]
- A/V ≥ 0,90 ; E0 = 37,4 [kWh/(m3rok)]
21. Składniki strat ciepła przy obliczaniu sezonowego
zapotrzebowania na ciepło do ogrzewania budynków
Straty ciepła przez przenikanie przez ściany zewnętrzne w
całym sezonie ogrzewczym:
![]()
[kWh/rok]
gdzie:
sD20 - liczba stopniodni okresu ogrzewania dla stacji meteorologicznej najbliższej
miejsca lokalizacji budynku,
Azi - pole powierzchni i - tej ściany zewnętrznej w świetle przegród prostopadłych
po odjęciu pól powierzchni drzwi i okien według wymiarów zewnętrznych
ościeżnic. [m2]
Uzi - współ. przenikania ciepła i - tej ściany zewnętrznej z uwzględnieniem wpływu
mostków termicznych [W/m2k]
Straty ciepła przez przenikanie przez okna w całym sezonie ogrzewczym:
![]()
[kWh/rok]
gdzie:
sD20 - jak we wzorze (4),
Aoi - pole powierzchni i - tego okna według zewnętrznych wymiarów ościeżnicy [m2],
Uoi - współ. przenikania ciepła okien w ścianie i - tej.
Straty ciepła przez przenikanie przez stropodach:
![]()
[kWh/rok]
gdzie:
Ad - pole powierzchni stropodachu w świetle przegród prostopadłych [m2],
Ud - współ. przenikania ciepła stropodachu z uwzględnieniem wpływu mostków termicznych [W/m2k].
Straty ciepła przez przenikanie przez strop nad piwnicą nie ogrzewaną:
Qsp = 0,024*SDsp*Asp*Usp [kWh/rok] (7)
gdzie:
SDsd - liczba stopniodni odpowiednia do obliczenia strat ciepła przez strop nad
piwnicą nie ogrzewaną ta. 1zał. 1[5]
Asp - pole powierzchni stropu nad piwnicą nie ogrzewaną w świetle przegród
prostopadłych [m2]
Usp - współ. przenikania ciepła z uwzględnieniem mostków termicznych, stropu nad
piwnicą nieogrzewaną
Straty ciepła do gruntu przez ściany i podłogę piwnic nie ogrzewanych.
Straty ciepła do gruntu przez podłogę na gruncie oblicza sie ze wzoru :
Qg = 0,024LD[Ls(20 - Tesp) + γ lp Ta) [kWh/rok] (8)
gdzie:
LD - długość sezonu grzewczego tab. 1 zał. 1[5]
Tesp - amplituda średnich miesięcznych temperatur powietrza zewnętrznego obliczam jako
połowa różnicy temperatury maksymalnej i minimalnej tab. 3 zał. 1[5]
γ - współczynnik zależny od długości sezonu ogrzewczego tab. 2 zał. 1[5]
Ls - współczynnik strat stałych w czasie [W/k]
Lp - współczynnik strat zmiennych w czasie [W/k]
Wielkości Ls i Lp są zdefiniowane w różny sposób w zależności
od sposobu izolacji podłogi.
Straty ciepła na ogrzewanie powietrza wentylacyjnego oblicza się:
Qv = 0,0082 ϕ SD23 [kWh/rok]
gdzie:
ϕ - strumień powietrza wentylacyjnego dla budynku [m3/h]
SD23 - liczba stopniodni odpowiednich do obliczenia strat ciepła na podgrzanie
powietrza wentylacyjnego tab. 1 zał. 1[5]
22. Składniki zysków ciepła przy obliczaniu sezonowego zapotrzebowania
na ciepło do ogrzewania budynków
Zyski ciepła od słońca przez szyby w całym sezonie grzewczym:
![]()
[kWh/rok]
gdzie:
Asi - pole powierzchni szyb w drzwiach ściany o i - tej orientacji
Tri - średnia ważona współczynnik przewodności promieniowania szyb, okien o orientacji i - tej tab. 5 zał. 1 [5]
zi - współ. zaciemnienia ścian w orientacji i - tej tab. 1,2 zał 2 [5]
si - suma promieniowania całkowitego na płaszczyźnie o orientacji i - tej w całym sezonie grzewczym tab. 6 zał. 1[5]
Wewnętrzne zyski ciepła od elektrycznych urządzeń oświetleniowych i od innych urządzeń elektrycznych, od ciepłej wody użytkowej, oraz od gotowania posiłków. Uwzględniamy zyski za pomocą wzoru:
Qp = 0,024 LD [80N + Lm (230 + ϕo3)] [kWh/rok]
gdzie:
LD - długość w dniach sezonu ogrzewczego tab. 1 zał. 1 [5]
N - ilość osób w budynku
Lm - liczba mieszkań w budynku
ϕo3 - uśredniona moc cieplna od oświetlenia okiennego do
jednego mieszka. tab7.Zał.1 [5]
23. Ciepłochłonność podłóg-zasady obliczania
Ciepłochłonność podłóg jest związana ze zjawiskiem zdolności oddawania ciepła przez żywy organizm do przedmiotów znajdujących się w otoczeniu przez stykające się z nimi. Jedną z form wymiany ciepła organ. z otoczeniem jest kontakt stopy ludzkiej z podłogą. Przeciętna powierzchnia stopy ludzkiej stanowi 2,3% w stosunku do całej powierzchni skóry, natomiast oddawanie ciepła jest 15x większe niż przez inne części
ciała ludzkiego.
Ssk= 1 ; Sst=0,023 ; Spsk=0,97
![]()
gst= ![]()
gst= ![]()
![]()
Dla uzyskania komfortu cieplnego podłogi we wszystkich pomieszczeniach przeznaczonych na pobyt ludzi, powinny charakteryzować się odpowiednią ciepłochłonnością niezależnie od wymagań w zakresie izolacyjności cieplnej.
Ciepłochłonność określa się za pomocą współczynnika ciepłochłonności β [Ws0,5/m2k]. Wartość współczynnika B przyjmujemy nie większe od Bmax.
B ≤ Bmax
gdzie:
B max - zależy od przeznaczenia pomieszczeń w przyjmuje się w następujący sposób:
1) w pomieszczeniach mieszkalnych B max=700[W·S0,5/m2k]
2) w pomieszczeniach na długotrwały pobyt ludzi B max=980
3) w pomieszczeniach produkcyjnych B max=1260
Współczynnik B określa się w następujący sposób:
Ciepłochłonność materiału wierzchniej warstwy może charakteryzować właściwości cieplne podłogi dla pewnego czasu To przy spełnionym warunku:
![]()
gdzie:
Fo - liczba Fouriera
Fogr - graniczna wartość liczby Fouriera
a1 - współczynnik wyrównania temperatur materiału
wierzchniej warstwy podłogi
![]()
gdzie:
λ - współczynnik przewodności cieplnej [W/m2k]
c1 - ciepło właściwe [Ws/kg k]
a1 - grubość wierzchniej warstwy podłogi w [m]
ρ1 - gęstość materiału wierzchniej warstwy [kg/m3]
Przyjmując graniczną wartość Fogr = 0,83 otrzymuje się warunek na grubość wierzchniej warstwy podłogi.
![]()
Przy spełnieniu tego warunku współczynnik ciepłochłonności: β = ξ1
ξ1 - aktywność cieplna materiału pierwszej warstwy
![]()
Jeżeli warunek (1) nie został spełniony to na ciepłochłonność
podłogi ma również wpływ materiał warstw położonych głębiej.
Warunek wpływu 1 i 2 warstwy ma postać:
![]()
Przy spełnieniu tego warunku β = ξ1A
gdzie:
zależy od stosunku ξ1/ξ2 z monogramu
E2-aktywnośc cieplna w 2 warstwy
Jeżeli warunek (2) nie został spełniony to na ciepłochłonność ma wpływ i trzecia warstwa czyli:
β = ξ2A1
gdzie:
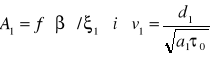
z monogramu
E3-aktywnośc cieplna 3 warstwy
24. Formy występowania wilgoci w materiałach budowlanych
Przy projektowaniu przegród budowlanych dąży się do max zabezpieczenia
przed możliwością jej zawilgocenia.
Zawilgocenie przegród budynku jest zjawiskiem niekorzystnym ze względu:
higieniczno-sanitarnych
niszczenia materiału w przegrodzie
zwiększenie strat ciepła
Zwiększenie strat ciepła wiąże się ze wzrostem λ materiałów zawilgoconych.
Niszczenie wiąże się z tym, że w materiałach pochodzenia niemoralnego
wzrost objętości wody przy przechodzeniu w łód powoduje uszkodzenie struktury wilgotnych materiałów porowatych, zwłaszcza przy wielokrotnym powtarzaniu cykli zamrażania i odmrażania. Również zmiany objętości towarzyszące zmianie wartości wody w przypadku wielokrotnego zawilgocenia wysychania materiałów prowadzi do ich stopniowego niszczenia.
Najniekorzystniejsze warunki występują w okresie zimy, gdy akumulacyjna wilgoć kondensacyjna przegród powstaje w wyniku dyfuzji pary jak i strat ciepła, przeprowadza się głównie dla tego okresu.
Wilgotność występuję w materiałach jako:
woda krystaliczna, w postaci cząsteczek hydratów. Wiązanie z materiałem jest najsilniejsze to jest chemiczne.
wilgoć sorpcyjna w postaci cząsteczek wody znajdujących się bezpośrednio na powierzchni ziaren, z którymi związana jest siłami wzajemnego oddziaływania cząstek, to jest siłami Van der Wallsa. Wiązanie z mat. jest fizyczno - chemiczne
Wilgoć kapilarna w postaci cieczy znajdującej się w porach i kapilarach, utrzymująca się na skutek napięcia powierzchni oraz sił związanych ze zjawiskiem zwilżenia materiału. Wiązanie z materiałem, jest fizyczno - mechaniczne.
Swobodna para wodna, przemieszczenie której odbywa się przez dyfuzję, filtrację i ruch molekularny.
Woda wolna przy nasyceniu przez bezpośrednie zetknięcie się materiału z wodą, przemieszczenie wody odbywa się wskutek podciągania kapilarnego, dyfuzji oraz filtracji wywołanej gradientem ciśnienia hydrostatycznego.
Decydujące znaczenie dla materiałów przegród ma woda sorpcyjna i kapilarna. Jeżeli materiał ma wilgotność wyższą od max sorpcyjnej to taki materiał nazywa się wilgotnym. Wilgotność przy pełnym nasyceniu jest z reguły kilkakrotnie większa od max wilgotności sorpcyjnej.
25.Wilgotnośc powietrza
Powietrze atmosferyczne można traktować jako mieszaninę suchego powietrza i pary wodnej. Para wodna wywiera pewne ciśnienie cząstkowe, które wraz z ciśnieniem cząstkowym suchego powietrza składa się na pełne ciśnienie atmosferyczne powietrza.
Rzeczywiste ciśnienie pary wodnej p [Pa] jest to ciśnienie cząstkowe pary wodnej zawartej w powietrzu nienasyconym przy określonej jego temperaturze i ciśnieniu atmosferycznym.
Ciśnienie cząsteczkowe pary wodnej może mieć dla danej temperatury wartość max i stan taki określa się pojęciem pary wodnej nasyconej ps [Pa]. Wartość ps zależy od temperatury powietrza, ze wzrostem zwiększa się, ze spadaniem maleje. Miarą nasycenia powietrza wilgocią jest wilgotność względna
![]()
gdzie:
ps - p - przyjmuje się przy tej samej temperatury i ciśnieniu powietrza
Im wyższa jest wilgotność względna powietrza tym jest powietrze bardziej wilgotne, a przy ϕ = 100% jest całkowicie nasycone parą wodną
Przy ochładzaniu przy stałej zawartości wilgoci. Wilgotność względna zwiększa się aż w pewnej temperaturze osiągnie 100%. W tym przypadku mamy powietrze całkowicie nasycone parą wodną. Temperatura stanu nasycenia jest temperaturą punktu rosy ts dalsze obniżanie temperatury spowoduje nadmiar wilgoci w powietrzu i para wodna będzie się skraplała.
Temperatura i wilgotność względna powietrza w budynkach zmieniają
się w szerokich granicach w zależności od temperatury i wilgotności względnej
i ciśnienia cząstkowego pary wodnej pomieszczenia dzielimy na: -suche
-średnio wilgotne
-wilgotne
-mokre
Średnia miesięczna wilgotność powierzchni zewnętrz, w Polsce w okresie
letnim =70% , w zimowym =85%
26. Przyczyny zawilgocenia przegród
Zawilgocenie przegród odbywa się w wyniku oddziaływania:
1) wilgoci budowlanej
2) wilgoci z opadów atmosferycznych
3) kapilarnego podciągania wody z gruntu
4) wilgoci sorpcyjnej
5) wilgoci kondensacyjnej
Wilgoć budowlana powstaje podczas wznoszenia nowych budynków w wyniku wykorzystywania mokrych procesów technologicznych wbudowania części materiałów w stanie dużego zawilgocenia.
Przegrody o zwiększonej wilgotności stosunkowo szybko wysychają do wilgotności ustabilizowanej. Zależy to od konstrukcji przegród i najczęściej nie przekracza 2-3 lat. W przypadku zastosowania od strony zewnętrznej przegrody materiału o dużym oporze dyfuzyjącym, czas wysychania może się wydłużyć. W początkowym okresie eksploatacji budynku należy się liczyć ze zwiększoną przewodnością ciepła przez przegrody a wiec ze zwiększonymi stratami ciepła w budynku.
27. Wilgoć z opadów atmosferycznych
Podczas intensywnych opadów atmosferycznych przy silnych wiatrach ukośnych po ścianach zewnętrznych spływają znaczne masy wody, w tym przypadku woda z opadów może wniknąć 10 - 20 cm w głąb przegrody. W okresach bezdeszczowych wilgoć w sposób naturalny wydyfuduje na zewnątrz. Szczelne pokrycie dachowe oraz pełne sprawne urządzenia do odprowadzania wód opadowych zabezpieczają budynek przed nadmiernym jego zawilgoceniem. W przypadku nieprawidłowo zaprojektowanych i wykonanych obróbek blacharskich lub ich uszkodzenia może nastąpić miejscowe zalane przegrody wodą i nadmierne zawilgocenie.
Zawilgocenie przegród pochodzące od opadów atmosferycznych może mieć istotniejsze znaczenie przy kumulowaniu się z innymi rodzajami zawilgocenia. W Polsce obserwuje się zwiększoną wilgotność w ścianach od strony zachodniej, tj. z kierunku najczęściej wiejących wiatrów.
Środkiem obrony przegród są:
stosowanie na zewnątrz warstwy przegród mat. o niskiej zdolności kapilarnego
podciągania wody
stosowanie wykładziny z blach fałdowanych ze szkła, i tym podobne..
28. Kapilarne podciąganie wody z gruntu
Zawilgocenie murów piwnicznych i piwnicznych kondygnacji w wyniku podciągania kapilarnego wody z gruntu powstaje przy braku izolacji przeciwwilgociowych, i uszkodzeniu lub naturalnym zużyciu izolacji w czasie wieloletniej eksploatacji budynku.
Wilgoć z gruntu może się podnieść na wysokość do 2,5 m od poziomu gruntu. Rozkład zawilgocenia na długość muru może być bardzo zróżnicowany, zarówno pod względem wysokości jak i stopnia zawilgocenia.
W budynkach nowo wznoszonych problem zawilgocenia przegród wodą z gruntu jest zlikwidowany przez wykonanie bitumicznych izolacji poziomych i pionowych
W budynkach istniejących wykonanie instalacji poziomej jest zabiegiem trudnym technicznie i bardzo kosztownym .Izolacje taką wykonuje się odcinkami ok. 1m przez podcinanie muru i zakładanie dwóch warstw papy na lepiku.
Najczęściej z powodu wysokich kosztów podcinania muru w budynkach istniejących dla zabezpieczenia przegród przed zawilgoceniem wodą z gruntu stosuje się:
wykonywanie wokół części podziemnej budynku ścianki murowanej lub betonowej uniemożliwiającej bezpośredni kontakt gruntu ze ścianami podpiwniczenia.
,,chowanie,, wilgoci przez wykonywanie wykładzin zakrywających
stosowanie otworów mających za zadanie wentylowanie określonego obszaru ściany.
wstrzykiwanie do morów środków chemicznych w celu zatkania porów i kapilar.
5) grawitacyjne wprowadzenie środka hydrofobizującego do muru
6) elektroinekcyjne osuszanie i blokowanie wilgoci w murach. Ostatnia metoda
zawiera 2 etapy:
założenie w zawilgoconym murze specjalnej instalacji elektroinekcyjnej, składającej się z elektrod dodatnich, ujemnych i urządzenia zasilającego prądem stałym. W taki sposób zapewnia się osuszanie i blokowanie wilgoci podciąganej kapilarnie przez mur????????????????????????
po obniżeniu wilgoci średniej W<10% wprowadza się do muru środek hydrofobowy. W taki sposób wytwarza się pozioma blokada nie pozwalająca na ponowne podciąganie wody z gruntu powyżej założonej blokady.
29. Wilgoć sorpcyjna
Sorpcja wilgoci- to proces pochłaniania pary wodnej z powietrza otaczającego materiał. Wskutek sorpcyjności materiały wykazują zawsze zawilgocenie zależne od wilgotności względnej otaczającego powietrza i temperatury. Zależność tą można
przedstawić graficznie w postaci tak zwane izotermy sorpcji.
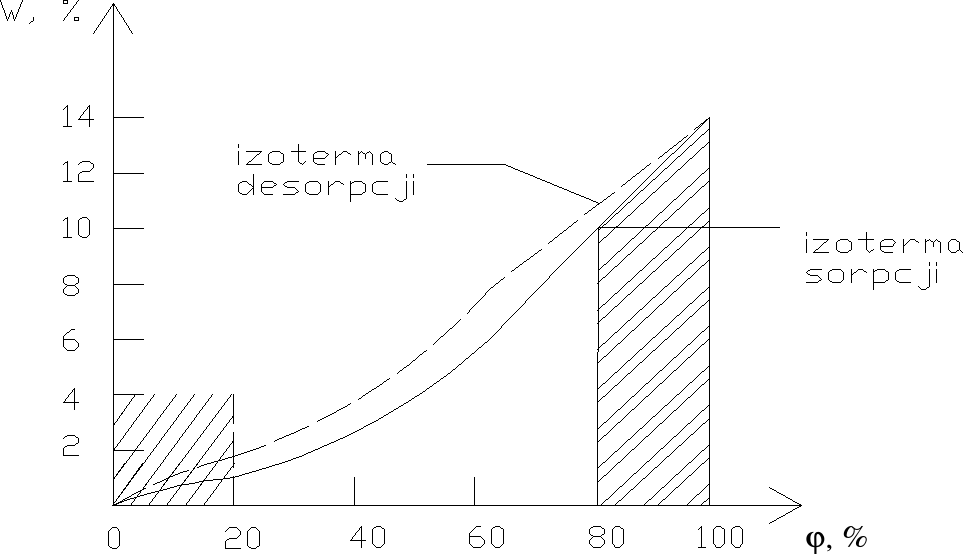
W zakresie ϕ = 0 ÷ 20% odbywa się zawilgocenie materiału przez wilgoć w postaci błonek monomolekularnych.
W zakresie ϕ =20 ÷ 80% odbywa się zawilgocenie materiału przez stworzenie błonek polimolekularnych.
W zakresie ϕ=80 ÷100% w porach i kapilarach materiałów powstaje kondensacja kapilarna. Na powierzchni porów i kapilarów tworzą się błonki w postaci cieczy.
Oddawanie wilgoci do powietrza przez materiał nadmiernie zawilgocony do stanu osiągnięcia równowagi sorpcyjnej nazywa się desorpcją.
Wilgotność sorpcyjna zależy oprócz temperatury i wilgotności względnej powietrza także od parametrów i struktury porów materiałów.
Ze wzrostem temperatury wilgotność sorpcyjna odpowiadająca tej samej wilgotności względnej powietrza maleje.
Wilgotność sorpcyjną najmniejszą mają ceramika, szkło, wełna mineralna, beton zwykły, gips (w<3%); największą wilgotność mają materiały drewnopochodne(w>30%)
Wilgoć sorpcyjna betonów zwykłych może istotnie wzrastać przy zastosowaniu
dodatków przeciwzamarzających ( betonowanie w okresie zimowym )
30. Zawilgocenie wskutek kondensacji pary wodnej
Para wodna znajdująca się w powietrzu może kondensować się na wewnętrznych powierzchniach oraz w wewnętrznych warstwach przegrody.
Kondensacja pary wodnej na powierzchni wewnętrznej przegrody może wystąpić wówczas, gdy temp. tych powierzchni będzie niższa od temp. punktu rosy. Vi<tr
![]()
Punkt rosy dla powietrza o znanej temp. i wilgoci względnej „ϕ” oblicza się w następujący sposób:
odnajduje się z tabel 1-16 (2) ciśnienie cząstkowe pary wodnej nasyconej ps, przy obliczeniowej temp. powietrza w pomieszczeniu ti
oblicza się ciśnienie pary wodnej nienasyconej „p” przy obliczeniowej wilgoci względnej powietrza w pomieszczeniu „ϕ” według wzoru
![]()
korzystając powtórnie z tabeli zależności ps=F(t) oraz przypuszczając, że p= ps określamy temperaturę punktu rosy(ts)
vi > tr, - to kondensacja nie występuje
v > tr - kondensacja występuje
Powstanie zjawiska kondensacji powierzchniowej zależy od izolacyjności termicznej przegrody wilgotności względnej ϕ i temperaturze powietrza zewnętrznego li.
Kondensacja na powierzchni przegrody najczęściej przy ϕi>75%.
W pomieszczeniach ϕi = 45÷60% zjawisko kondensacji może wystąpić na powierzchni ścian o niedostatecznej izolacyjności termicznej oraz w miejscach mostków termicznych i narożach. Wilgoć kondensacyjna na powierzchni wnika w materiał przegrody wskutek podciągania kapilarnego i dlatego wilgotność przegród zwiększa się. W pomieszczeniach ϕi >75% powierzchnie przegród powinny być zabezpieczone szczelnymi wykładzinami lub powłokami nieprzepuszczającymi wodę.
W czasie obecnym w Polsce opracowana norma zgodnie z europ. ENISO 13788
według której projektuję się przegrody budowlane pod kierunkiem uniknięcia rozwoju pleśni
Główną zasadą tego podejścia jest to, że aby uniknąć rozwoju pleśni wilgotność
względna na powierzchni przegrody nie powinna przekraczać wartości 80% przez kilka dni.
Główne kroki procedury projektowej są to:
1) określenie ciśnienia rzeczywistego pary wodnej w powietrzu wewnętrznym.
Mamy ti, ρi, z tabeli określamy ps ,stąd P= ps· ρi / 100
2) określenie ciśnienia pary wodnej nasyconej(Psat) na powierzchni przegrody
z uwzględnieniem wymaganej wilgotności względnej: 80% na powierzchni tej sciany.
Psat= p/ 0,8
określenie minimalnej temperatury powierzchni wewnętrznej ściany zewnętrznej
za pomocą tabeli ps=F(t) , w sposób odwrotny z uwzględnieniem, że ps=psat
υi min= F(psat)
na podstawie υi min i znanych temperatur powietrza wewnętrznego i zewnętrznego(ti i te) obliczamy minimalną wartość czynnika temperaturowego
![]()
procedura ta jest wykonywana dla każdego miesiąca w roku, z odpowiednimi
dla tych miesięcy temperaturami i wilgotnościami powietrza zewnętrznego ściany, w celu
uniknięcia pleśni, należy tak projektować by dla krytycznego miesiąca frs>frsi,min, gdzie:
![]()
31. Zawilgocenie przegród w skutek dyfuzji i kondensacji pary wodnej
Dyfuzja pary wodnej przez przegrody budowlane odbywa się w wyniku różnic ciśnień cząsteczek pary wodnej w pomieszczeniu i na zewnątrz budynku.
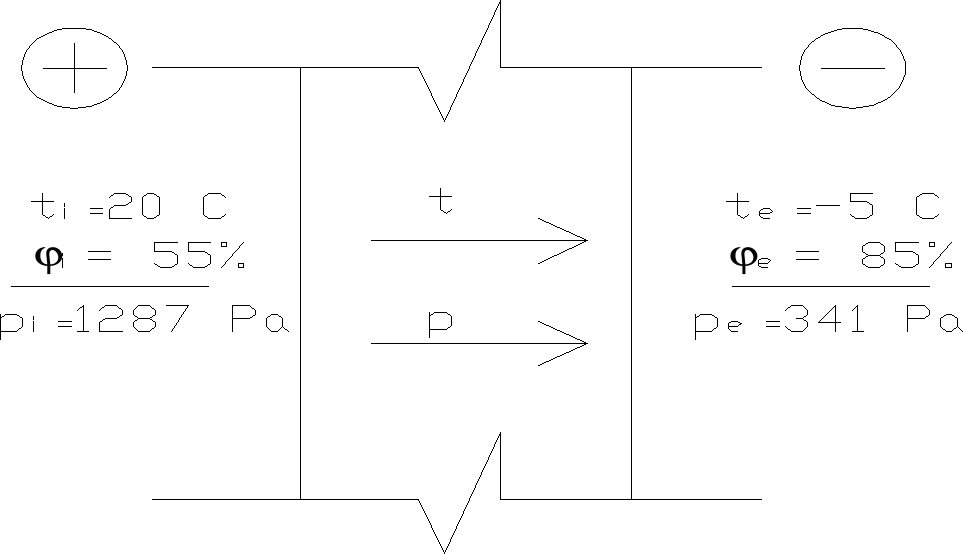
Dyfundująca przez przegrodę para wodna może ulegać kondensacji w określonym obszarze tej przegrody i powodować zawilgocenie materiałów znajdujących się w strefie kondensacji.
Przy projektowaniu przegród należy brać pod uwagę możliwość powstawania tych zjawisk i nie dopuszczać do nadmiernego zawilgocenia.
Metody obliczenia wielkości zawilgocenia przegród opierają się na założeniu, że wilgoć przemieszcza się tylko w postaci pary wodnej.
Gęstość strumienia dyfundującej pary wodnej:
![]()
gdzie:
![]()
= 2* 10-10 [![]()
- paroprzepuszczalność powietrza w odniesieniu do ciśnienia cząstkowego pary wodnej
![]()
- różnica ciśnień pary wodnej
Sd= ![]()
*d- dyfuzyjnie równoważna grubość warstwy nieruchomego powietrza[m]
![]()
- współczynnik oporu dyfuzyjnego materiału odpowiedniej warstwy (według tabeli normy dla odpowiedniego materiału)
d- grubość warstwy materiały [m]
![]()
; ![]()
- paroprzepuszczalność materiału w odniesieniu do ciśnienia cząstkowego pary wodnej
W praktyce obliczeń rozpatruje się dyfuzję pary wodnej w warunkach ustalonych, co znacznie upraszcza obliczenia.
Dyfuzja pary wodnej jest procesem przebiegającym stosunkowo powoli, stąd temperatura i wilgotność powietrza przyjmuje się jako średnie wartości miesiąców, dla których wykonywane są obliczenia.
Początek kondensacji zależy nie tylko od temperatury i wilgotności powietrza po obu stronach przegrody, ale też od konstrukcji przegrody, czyli układu warstw i rodzaju użytych materiałów. Gdy warstwa szczelna, o dużym oporze dyfuzyjnym, usytuowane są od strony zewnętrznej przegrody wówczas taki rozkład jest niekorzystny. Proces kondensacji występuje wtedy szybciej i trwa dłużej w porównaniu z przegrodami o odwrotnym układzie warstw.
32. Obliczanie wewnętrznej kondensacji w ścianach zewnętrznych
Do obliczenia wewnętrznej kondensacji podaną metodą rocznego określenia wilgoci oraz obliczenia maksymalnej ilości wilgoci zakumulowanej z powodu kondensacji wewnętrznej. W metodzie tej zakłada się, że cała wilgoć budowlana wyschła.
Oblicza się wielkość kondensacji lub odparowania w każdym z 12 miesięcy w roku.
Masa wody powstałej w wyniku kondensacji zakumulowana pod koniec miesiąca, w którym kondensacja się pojawiła jest porównywana z całkowitym odparowaniem w ciągu pozostałej części roku. Zakłada się przypadek jednowymiarowy i warunki stanu ustalonego.
Przy obliczaniu należy stosować następującą procedurę:
Podzielić ścianę zewnętrzna na szereg równoległych, jednorodnych warstw i w każdej z nich zdefiniować właściwości materiału według odpowiedniej tabeli normy.

λ1, λ2, λ3, (λj)
μ1, μ 2, μ 3, (μ j)
Dla każdej oddzielnej warstwy ściany obliczyć opór cieplny Rj i gubość warstwy nieruchomego powietrza Sdj, która ma taki sam opór dyfuzyjny jak rozważana warstwa materiału
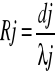
; Sdj= μj- dj
Obliczyć narastający opór cieplny i grubość warstwy nieruchomego powietrza o takim samym oporze dyfuzyjnym od strony zewnętrznej do każdej powierzchni stykowej n:
![]()
![]()
Obliczyć całkowity opór cieplny i grubość warstwy nieruchomego powietrza o takim samym oporze dyfuzyjnym
![]()
![]()
Dla każdego miesiąca w roku poczynając od miesiąca początkowego (zwykle dwa miesiące przed najchłodniejszym okresem), obliczyć temperaturę na każdej powierzchni styku materiału
![]()
Mając temperaturę ![]()
oraz korzystając z tabeli zależności ps=f(t) określić ciśnienie pary wodnej nasyconej (ps) na każdej powierzchni styku materiału.
Narysować przekrój ściany z grubościami warstw równoważnymi ich dyfuzyjnie równoważnym grubościom warstwy powietrza Sdj oraz narysować linie proste łączące wartości ciśnienia pary nasyconej na każdą powierzchnię styku materiałów. Narysować profil ciśnienia rzeczywistego pary wodnej jako linię prostą, łączącą wewnętrzne i zewnętrzne wartości pi i pe
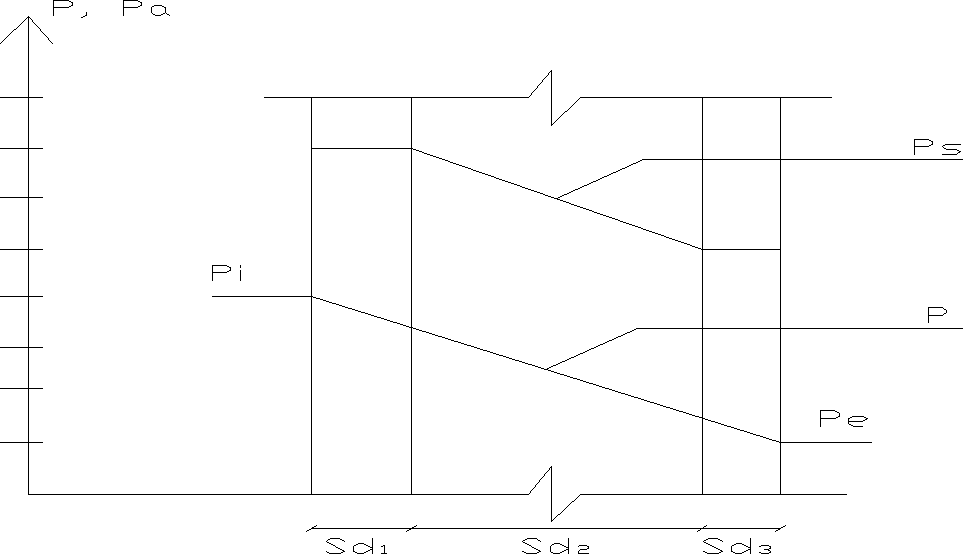
Jeżeli linia p nie przekracza linii ps na żadnej z powierzchni styku, kondensacja w środku przegrody nie wystąpi. Strumień pary wodnej przepływający przez ścianę w takiej sytuacji oblicza się ze wzoru:
![]()
Jeżeli ciśnienie pary wodnej (p) przekracza wartość ciśnienia pary nasyconej (ps), na którejkolwiek powierzchni styku, należy wykreślić ciśnienie pary w postaci szeregu linii, które stykają się z profilem ciśnienia pary nasyconej, ale go nie przekraczają. Punkty te wskazują powierzchnie styku, na których wystąpi kondensacja.
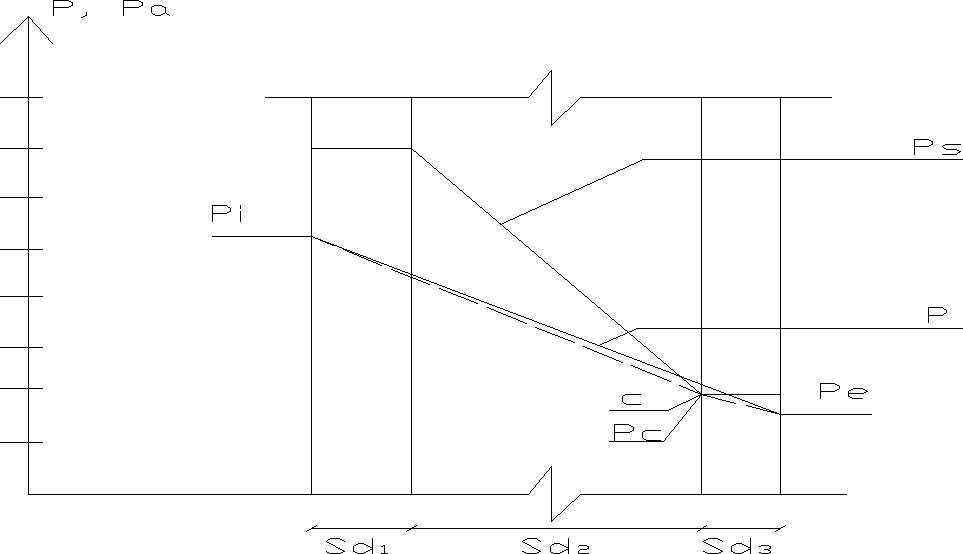
W danym przykładzie to punkt c. Strumień kondensacyjny dla takiej sytuacji jest różnicą między ilością wilgoci przenoszonej do powierzchni stykowej i od powierzchni stykowej na zewnątrz:
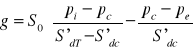
10) Jeżeli na którejkolwiek powierzchni styku istnieje kondensat zakumulowany w poprzednich miesiącach, ciśnienie rzeczywiste pary wodnej powinno być równe ciśnieniu pary nasyconej, a profil ciśnienia pary ma postać:
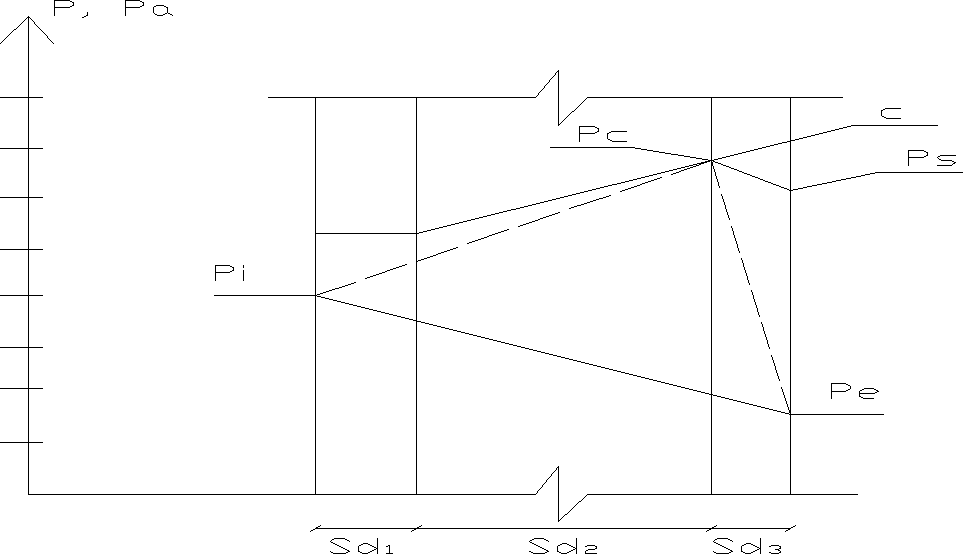
W takiej sytuacji mamy strumień porowania:
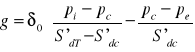
Wyrażenia na strumień kondensacji i porowania są takie same. Umownie kondensacja pojawia się, gdy wyrażenie jest dodatnie, a porowanie-, gdy wyrażenie jest ujemne.
11) Na podstawie wyniku obliczeń należy ocenić konstrukcje w ścianie:
a) jeżeli nie przewiduje się kondensacji na żadnej powierzchni stykowej w żadnym miesiącu to należy określić konstrukcje ściany jako wolną od wewnętrznych kondensacji
b) jeżeli kondensacja występuje, na którejkolwiek powierzchni stykowej, ale przewiduje się wyparowanie kondensatu podczas miesięcy letnich, to należy podać maksymalną ilość kondensatu, w tej powierzchni oraz miesiąc w którym wystąpi maksimum. Należy też rozważyć ryzyko degradacji materiałów ściennych i ryzyko pogorszenia właściwości cieplnych w wyniku zawilgocenia przegrody
c) jeżeli kondensacja nie wyparowuje całkowicie podczas miesięcy letnich, należy przeprojektować ścianę, a mianowicie zmienić układ warstw czy zastosować na jej powierzchni wewnętrznej izolację. To są powłoki z pary olejowej emalii, lakieru( pojedyncze, podwójne lub potrójne). Mogą stosować się również folie polietylenowe.
33. Wysychanie przegród budowlanych z wilgoci początkowej
W przegrodach wykonywanych technologią mokrą wilgotność początkowa materiałów jest znacznie wyższa od maksymalnej wilgotności sorpcyjnej i często bliska nasyceniu materiałów. Ruch wilgoci w tym zakresie wilgotności jest, więc wywołany siłami podciągania kapilarnego.
Energie wiązania wody kapilarnie zwięzanej jest niewielka, stąd też wysychanie wilgoci z powierzchni materiału wilgotnego odbywa się tak jak ze swobodnej powierzchni cieczy.
Ale po wysychaniu powierzchni materiału szybkość wysychania maleje. Proces suszenia dzielimy na dwa okresy:
1) Okres stałej prędkości wysychania, w którym gęstość strumienia masy na powierzchni przegrody zależy tylko od warunków otoczenia. Wilgotność materiałów na powierzchni jest większa lub równa maksymalnej wilgotności sorpcyjnej.
2) Okres malejący szybkości wysychania, który wyrażamy równaniami:
![]()
gdzie:
u-wilgotnośćmateriału
τ- czas
k- współczynnik suszarniczy ![]()
- średnia wilgotność po grubości elementów
us- maksymalna wilgotność sorpcyjna
uk- wilgotność krytyczna odpowiadająca przejściu od pierwszego do drugiego okresu wysychania
Zależność szybkości wysychania w funkcji wilgotności materiału przedstawiamy graficznie
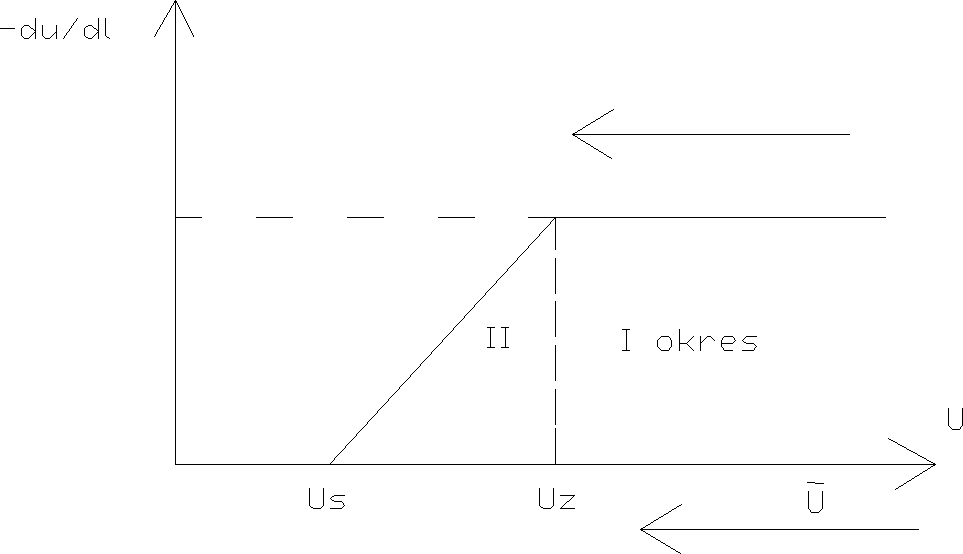
Zmniejszenie prędkości suszenia w II okresie wywołane jest wyschnięciem całej powierzchni materiału i cofnięciem się powierzchni odparowania w głąb materiału. Wtedy dochodzi opór dyfuzji pary wodnej przez suchą warstwę materiału, co zmniejsza szybkość wysychania.
Dla płyty nieskończonej odsychającej dwustronnie w stałych warunkach wysychania zapisujemy:
![]()
gdzie:
![]()
- średnia wilgotność krytyczna
us-maksymalna wilgotność sorpcyjna
g0- strumień wysychający wilgoci w I okresie
d- połowa grubości schnącego elementu
am- współczynnik dyfuzji wilgoci w materiale
δ- gęstość materiału
Ze wzoru wynika, że dla danego materiału przy znanych am i δ różnica między średnią wilgotnością, a wilgotnością pod koniec I okresu wysychania zależy od szybkości suszenia g0:
- im szybsze jest suszenie w I okresie tym bardziej niejednorodny jest rozkład wilgotności oraz większa różnica wilgotności na grubości ściany wystąpi w przegrodach z materiałów o mniejszym am i δ.
Ponieważ ruch wilgoci w materiałach w I okresie suszenia odbywa się głównie pod wpływem sił kapilarnych to im jest większa szybkość podciągania kapilarnego tym szybsze wysychanie materiału.
Szczelne warstwy okładzinowe znacznie hamują wysychanie, w których od
zewnątrz występuje szczelne pokrycie papowe, a od wewnątrz warstwa betonu i izolacja
parościenna. Duża podłoża może spowodować niszczenie pokrycia papowego.
34. Ogólne wiadomości o dźwięku
Dźwięk jest zjawiskiem falowym wywołanym drganiami cząstek dowolnego ośrodka. W zależności od ośrodka rozprzestrzenianie się fal akustycznych (dźwięków) dzielimy na:
1) powietrzne (rozprzestrzeniające się w powietrzu)
2)uderzeniowe (materiałowe).
Wielkościami charakterystycznymi fali dźwiękowej są:
częstotliwość f[Hz] jest to liczba okresów drgań w ciągu t [s],
długość λ [m] jest to odległość jaką przebywa fala akustyczna w czasie jednego okresu drgań T [s],
prędkość rozchodzenia się fali dźwiękowej c [m/s].
Wielkość λ związana jest zależnością:
![]()
Ze względu na częstotliwość i związaną z nią długość fali akustycznej dźwięki dzieli się na:
infradźwięki (f < 16 Hz; λ > 21 m)
dźwięki słyszalne (f = 16 do 20000 Hz, λ > 1,7 do 21 m)
ultradźwięki (f > 20000 Hz, λ < 1,7 m).
Prędkość dźwięku w powietrzu c=340m/s. W ciałach stałych prędkość zależy od cech sprężystych materiału i kształtu elementu.
Każde źródło dźwięku charakteryzuje się mocą akustyczną Pa [W]. W technicznych obliczeniach stosuje się pojęcie poziomu mocy akustycznej Lp
Lp'=10 log ![]()
[dB]
gdzie:
PΔ - moc akustyczna źródła [W]
P0 - moc akustyczna odniesienia
Po = 10-12 [W]
W praktyce pomiary stosuje się pojęcie ciśnienia (poziom ciśnienia akustycznego). Ciśnienie akustyczne Pa [N/m2] w powietrzu jest to różnica między chwilową różnicą ciśnienia powstałego w danym punkcie pola pod działaniem fal akustycznych, a wartością ciśnienia statycznego.
Poziom ciśnienia akustycznego Lp:
Lp= 10 log![]()
[dB].
gdzie:
Po - ciśnienie akustyczne odniesienia
Po= 2*10-5 [N/m2].
35. Dopuszczalne poziomy dźwięków w pomieszczeniach
Do scharakteryzowania i oceny hałasu w praktyce stosuje się najczęściej poziomy dźwięków. Poziom dźwięku jest to wypadkowa skorygowanych poziomów ciśnienia akustycznego danego sygnału akustycznego w poszczególnych pasmach częstotliwości.
Koordynowanie poziomów ciśnienia ma na celu przybliżenie wyników pomiarów lub obliczeń do wrażenia słuchowego odbieranego przez ucho.
Poziom dźwięku LAi może być oceniany przez bezpośredni pomiar hałasu miernikiem. Średni poziom dźwięku LAm można obliczyć:
LAm=![]()
![]()
gdzie:
n- liczba określonych pomiarów dźwięku w czasie obserwacji.
Równoważny poziom dźwięku LAeg obliczyć można:
![]()
[dB]
gdzie:
T- czas oceny
Ti- czas, w którym poziom dźwięku jest występujący w czasie ,w którym hałas można uznać za ustalony ( to hałas, którego poziom dźwięku w określonym punkcie zmienia się w czasie max o 5 dB)
T1-czas, w którym poziom dźwięku jest ustalony i wynosi:
LAi ,przy czym Σti=T
Wielkością istotną dla określenia dopuszczalnych wartości poziomu dźwięku w pomieszczeniu jest max poziom dźwięku LAmax to znaczy max wartość skuteczna poziomu dźwięku występujących podczas obserwacji.
Dopuszczalny poziom dźwięku hałasu przenikającego do pomieszczenia przeznaczonego na pobyt ludzi (LAB*, Leg*, LAmax*) należy przyjmować wg normy „Akustyka budowlana” przy spełnieniu warunków:
LAmax![]()
LAmax*
LAeg![]()
LAeg*
LAm![]()
LAm*
Przy niespełnieniu warunków stosujemy ochronę przeciwdźwiękową polegającą na:
zmniejszeniu poziomu hałasu wytworzonego przez źródło
ograniczenie dróg rozprzestrzeniania się hałasu
Uzyskuje się to poprzez:
a) oddalenie budynku od istniejących źródeł hałasu zewnętrznego.
b) rozplanowanie pomieszczeń w budynku z uwzględnieniem źródła hałasu.
c) zastosowanie okien o dobrych właściwościach akustycznych (np. trój szybowe).
d) zastosowanie ścian i stropów o odpowiednich właściwościach akustycznych.
e) lokalizacja pomieszczeń technicznych z dala od pomieszczeń użytkowych.
f) Izolacja instalacji pod względem akustycznym.
36. Wymagania izolacyjności akustyczna przegród i elementów budowlanych
Zgodnie z normą ,,akustyka budowlana,, , ściany zewnętrzne i wewnętrzne, okna i drzwi powinny charakteryzować się izolacyjnością od dźwięków powietrznych oraz izolacyjnością od dźwięków uderzeń.
Izolacyjność akustyczną przegród w budynkach określa się za pomocą
wskaźników jedno liczbowych:
Ważony wskaźnik izolacyjności akustycznej właściwej, przybliżonej Rw' (dla ścian wewnętrznych, stropów, drzwi, okien wewnętrznych) lub R''tr,w (dla ścian i okien zewnętrznych) [dB].
Ważony wskaźnik poziomu uderzeniowego znormalizowanego przybliżonego L'n'w (dla stropów) [dB].
Rw=R'w-c c,4-uwzględniają boczne przenoszenie energii akustycznej
.
R''tr,w> R'tr,w(min),
Ln,w= L'n,w + 4
R'n,w(max) Rw, Rtr, Lw, króre związane są z wielkościami wskaźników Rw, Rtr,w', L'n,w w następującch zależnościach:
- dla ścian zewnętrznych i stropów
- dla stropów
- dla drzwi wewnętrznych Rw= Rw'
- dla ścian zewnętrznych Rw= R'tr,w
Przenoszenie boczne składa się z przenikania energii elektrycznej drogami:
Przez nieszczelności przegrody.
Przez przewody instalacyjne.
Przez przestrzeń poza przegrodą
Drogami materiałowymi za pośrednictwem przegród bocznych.
Przy prawidłowym projektowaniu i wykonaniu budynku następować,przenoszenie boczne budynku = przenoszeniu bocznemu tylko drogami materiałowymi
Przegrody projektujemy tak by zostały spełnione warunki:
Rw' >Rtr(min)
Rtr,w'> Rtr,w'(min)
L'n,w < L'n,w(min)
Rtr(min) ![]()
L'n,w(min) Wartości normowe
Rtr,w'(min)
w zależności od przeznaczenia budynku i funkcji pomieszczeń budynku.
37. Obliczenie wskaźników jedno liczbowych izolacyjności od dźwięków
powietrznych
Izolacyjność przegród od dźwięków powietrznych można wyznaczyć ze wzoru:
R= 10log![]()
[dB].
gdzie:
W1- moc akustyczna padająca na przegrodę [W].
W2- moc akustyczna przenoszona przez przegrodę do drugiego pomieszczenia[W].
Jeżeli przegroda rozdziela dwa pomieszczenia w których pole akustyczne może być uznane za rozproszone, a energia przenika z pomieszczenia do pomieszczeń wyłącznie przez rozpatrywaną przegrodę, to izolacyjność akustyczną można wyznaczyć z zależności:
R= L1 - L2 + 10log ![]()
[dB].
gdzie:
L1- poziom przeciętnego ciśnienia akustycznego w pomierzeniach ze źródłem dźwięku [dB].
L2- jw. lecz w pomieszczeniach za przegrodą [dB].
S- wielkość powierzchni przegrody [m2].
A - chłonność akustyczna pomieszczenia odbiorczego za przegrodą [m2].
A= ![]()
![]()
gdzie:
V- objętość pomieszczenia [m3].
T- czas pogłosu pomieszczenia [s].
Wzór (1) jest wygodny dla praktycznego stosowania.
L1 i L2 mogą być wyznaczone w warunkach laboratoryjnych.
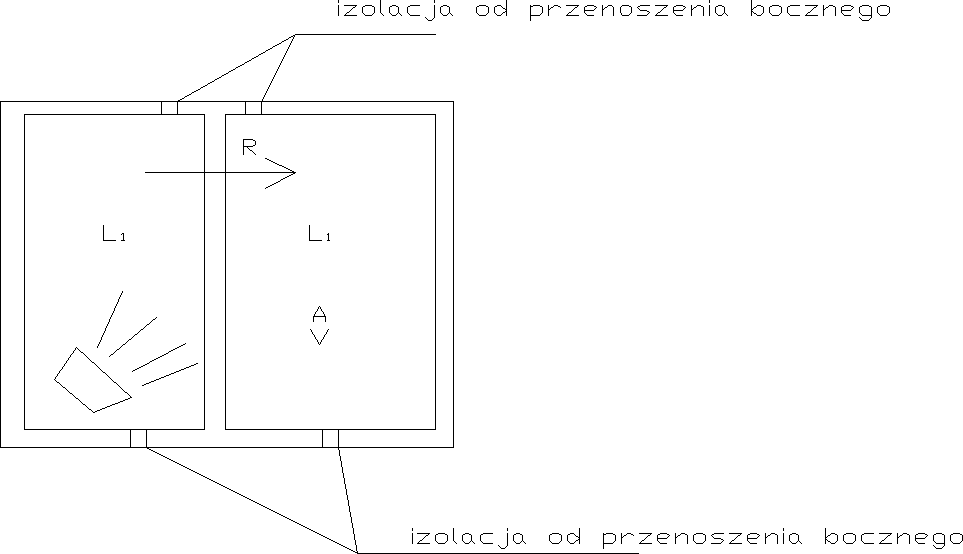
W przypadku nie zapewnienia przenikania całej energii z pomieszczenia nadawczego do odbiorczego przez badaną przegrodę (w zasadzie dzieje się tak zawsze w warunkach innych niż laboratoryjne) możemy mówić o izolacyjności akustycznej właściwej przybliżonej, wyznaczamy w warunkach występowania przenoszenia bocznego, którą oblicza się ze wzoru;
R'= L1'-L2'+10log![]()
[dB].
R', L1', L2'- jw. lecz obarczone wpływem przenoszenia bocznego.
Według obecnej formy z akustyki izolacyjnej w budynkach mieszkalnych i użytkowych publicznej określają wskaźniki ważone Rw, Rw' lubMa, Ma'
Pomiędzy wskaźnikami względnymi a ważonymi występuje zależność:
Ma= Rw - 52 [dB].
Ma'= Rw'- 52 [dB].
Wyznaczenie wskaźników polega na porównaniu wartości izolacyjności od dźwięków powietrznych, zmierzonych z wartościami odniesienia dla poszczególnych pasm częstotliwości pasmowych w przedziale 100![]()
3150 [Hz].
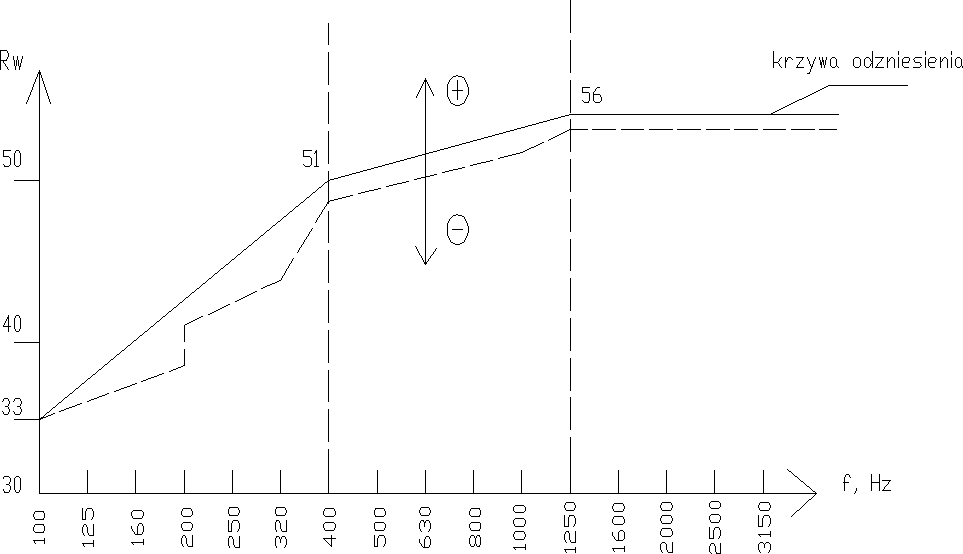
Aby ocenić wyniki pomiarów przesuwa się skokowo o 1 [dB] krzywą odniesienia [1] w kierunku linii uzyskanej z pomiarów [2].Przesuwanie następuje do momentu aż średnie niekorzystne odchyłki (wartości bezwzględne) będzie maksymalnie duże, lecz > 2 [dB]. Średnie niekorzystne odchylenie oblicza się ze wzoru:
(δśr)= ![]()
[dB].
gdzie:
δi - niekorzystne odchylenie krzywej pomiarowej od krzywej odniesienia [dB].
n - liczba niekorzystnych odchyleń we wszystkich pasmach pomiarowych.
Odchylenie niekorzystne w danym paśmie częstotliwości występuje wtedy, gdy wyniki pomiaru w tym paśmie są mniejsze od wartości odniesienia. Do obliczeń ![]()
bierze się wyłącznie odchylenie niekorzystne.
Jako wskaźnik ważony izolacyjności akustycznej właściwej dźwięków powietrznych Rw przyjmuje się rzędną krzywej odniesienia (przesunięty) dla częstotliwości 500 [Hz].
Wskaźnikiem względnym Ma jest liczba decybeli o jaką przesunięto krzywą odniesienia. Przy czym wskaźnik Ma jest dodatni, gdy przesunięcie nastąpiło w kierunku izolacyjności korzystniejszych, a ujemną gdy w kierunku niekorzystniejszych (w stosunku do pierwotnego położenia krzywej odniesienia).
38. Obliczenie wskaźników jedno liczbowych izolacyjności od dźwięków
uderzeniowych
Izolacyjność stropów od dźwięków uderzeniowych lub tłumienie dźwięków uderzeniowych jest wielkością względną, określoną przez znormalizowany poziom dźwięków uderzeniowych pod stropem przy pobudzaniu stropu znormalizowanym źródłem dźwięków uderzeniowych. Znormalizowany poziom uderzeniowy wyznacza się w pasmach tercjowych z zależności:
Ln= Lit10log![]()
[dB]
gdzie:
Li= poziom przeciętnego ciśnienia akustycznego pod stropem w pasmach tercyjnych przy pracującym na stropie znormalizowanym źródeł dźwięku [dB].
A- chłonność akustyczna pomieszczenia odbiorczego wg wzoru:
A=![]()
[dB].
A0 - chłonność akustyczna ciśnienia A0= 10m2.
Przykład występowania przenoszenia bocznego należy obliczyć znormalizowany poziom uderzenia Wy przybliżony Ln' ze wzoru:
Ln'= Li'+10log![]()
[dB].
gdzie:
Li'- zgodnie z w/w zależnością, ale wyznaczane w warunkach przenoszenia bocznego.
Według obecnej normy izolacyjność od dźwięków uderzeniowych w budynkach
mieszkalnych i użytkach publicznej określają Mi, Mi;- względny lub Ln,Ln'- ważony
Wskaźnik względny Mi jest to wielkość w dB o jaką należy przesunąć krzywą odniesienia, aby spełnione były warunki opisane poniżej
Wskaźniki są ze sobą powiązane następującymi zależnościami:
Mi= 60- Ln,w [dB.
Mi= 60-Ln,w' [dB]
Wyznaczenie wskaźników Ln,w, Mi, Mi', Ln,w, polega na porównaniu krzywej uzyskanej z pomiarów w poszczególnych pasmach częstotliwości z krzywą odniesienia.
wykres
Aby ocenić wyniki pomiarów przesuwa się skokowo co 1 [dB] krzywą odniesienia w kierunku linii uzyskanej z pomiarów. Przesunięcie następuje do momentu, aż średnie niekorzystne odchylenie ![]()
będzie maksymalnie duże, lecz mniejsze od 2 [dB].
Odchylenie niekorzystne występuje wtedy, gdy wynik pomiaru jest większy od wartości odniesienia, tj. tok postępowania podczas wyznaczania wskaźników Mi, Ln,w, jest identyczny jak wyznaczanie wskaźników Ma, Rw.
Różnica polega na tym, iż w tym przypadku izolacyjności lepsze reprezentowane przez wyniki pomiarów, niższe od odpowiednich rzędnych krzywych odniesienia. Odpowiednio izolacyjności gorszej odpowiadającym większym od rzędnych krzywej odniesienia wynikom pomiarów.
39. Podstawy teoretyczne izolacyjności akustycznej przegród budowlanych
Przenikanie energii akustycznej przez przegrodę odbywa się głównie wskutek drgań przegrody jako całości. Drgania przegrody zależą nie tylko od cech samej przegrody, ale również:
Przy padaniu energii akustycznej pod kątem θ, gdzie:
0°![]()
θ ![]()
90°,
izolacyjność płyt R określa się wzorem:
R= 20logf+ 20logm- 47.5 [dB].
gdzie:
f- częstotliwość dźwięku [Hz].
M- masa przegrody przypadająca na jednostkę powierzchni [kg/m2].
Prędkość fali akustycznej padającej na przegrodę pod ![]()
θ może być rozłożona
na dwie składowe.
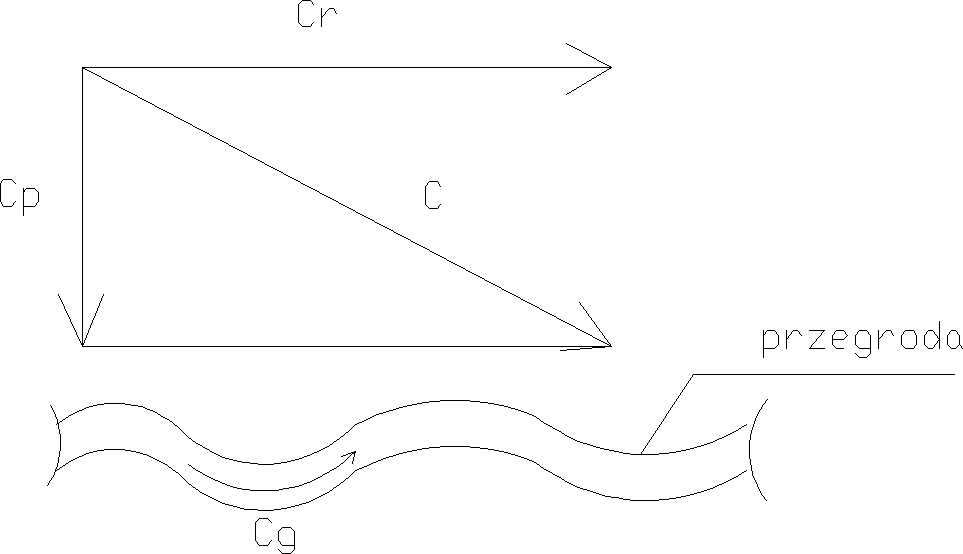
Wynik działania składowej równoległej do przegrody, w przegrodzie powstają fale gięte. Jeżeli prędkość fal giętych Cg w płycie jest równa składowej Cr, prędkość fali dźwiękowej padająca pod kątem θ, to między ośrodkiem a przegrodą zachodzi zjawisko rezonansu przestrzennego, tzw. zjawisko koincydencji. W wyniku tego następuje wzrost drgań przegrody i znaczne obniżenie izolacyjności.
Zjawisko koincydencji może występować przy każdej częstotliwości powyżej częstotliwości granicznej przegrody wyrażonej wzorem:
fgr= 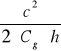
gdzie:
c- prędkość dźwięku w powietrzu [m/s].
Cg- prędkość dźwięku w przegrodzie [m/s].
h- grubość przegrody [m].
Schematyczną charakterystykę izolacyjności akustycznej przegrody z uwzględnieniem zjawiska koincydencji pokazano na rysunku:
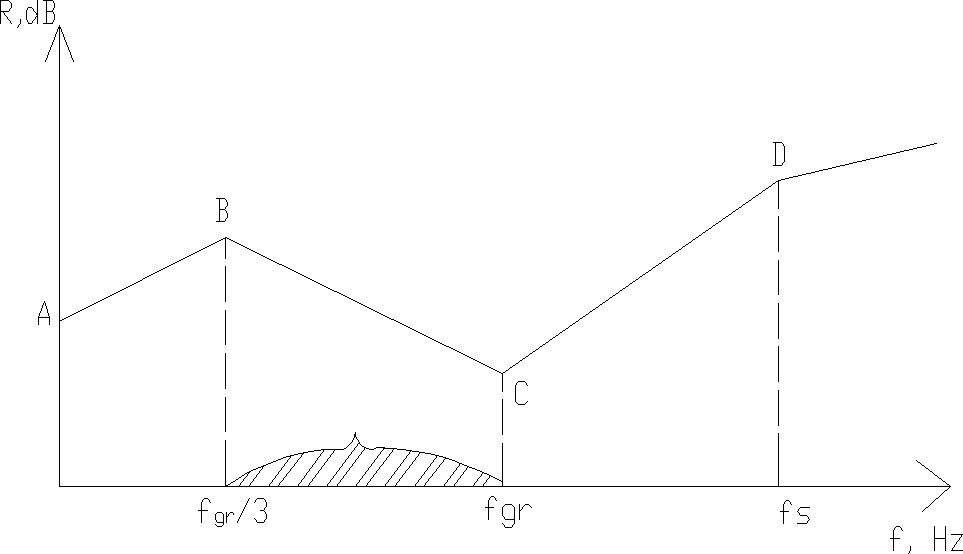
Przy f![]()
![]()
fgr izolacyjność akustyczna opisana jest wzorem (4).
Przy ![]()
fgr<f<fgr izolacyjność przegrody nie jest określona żadnym wzorem teoretycznym.
Przy fgr![]()
f<fs izolacyjność wyrażona jest wzorem:
R= R0+10log2η![]()
gdzie:
R0- izolacyjność wg wzoru (4)
η- współczynnik tłumienia wewnętrznego w materiale przegrody (dla betonu
η= (4![]()
8)∙10-3).
W przypadku płyt grubych w płycie powstają fale ścinające, które powodują zahamowanie wzrostu izolacyjności. Częstotliwość graniczna, przy której staje się dominujący udział fal ścinających w płytach jednorodnych określona jest wzorem:
Fs= ![]()
gdzie:
Przy f>fs izolacyjność określona jest wzorem:
????????????
40. Właściwości akustyczne przegród budowlanych
Charakterystyka izolacyjności akustycznej ścian wewnętrznych z betonu, cegły, gipsu, gazobetonu uwidoczniają się wszystkie zjawiska opisane w pkt.39
1) W przypadku płyt cienkich kształt krzywej izolacyjności jest bardziej zbliżony do teoretycznego niż w przypadku płyt grubych. Związane jest to z dodatkowym wpływem grubości i sztywności przegrody.
Przy tej samej masie 1m2 przegrody z betonów lekkich kruszywowych (keramzytobeton) charakteryzuje się nieco większym wskaźnikiem izolacyjności akustycznej niż przegrody z betonu żwirowego.
Nieco gorsze od przegród z betonu żwirowego właściwości akustyczne wykazują przegrody gipsowe, a przede wszystkim przegrody gazobetonowe.
Przegrody płytowe zapewniają izolacyjność wymaganą dla ścian między mieszkaniowych przy grubości:
h= 15cm - z betonu żwirowego (![]()
= 2400 kg/m3).
h= 18cm - z betonu lekkiego (![]()
= 1600 kg/m3).
W celu uzyskania większej izolacyjności akustycznej przy mniejszej masie 1m2 przegrody stosuje się przegrody podwójne.
Przegrody lekkie warstwowe uzyskuje się przy sklejeniu warstw materiału o zróżnicowanych właściwościach fizycznych.
Zysk izolacyjności, spowodowany wielowarstwowością przegrody, występuje tylko w ograniczonym paśmie częstotliwości.
Z punktu widzenia akustycznego przegrody warstwowe dzielimy na dwie grupy:
przegrody sztywne (np. ściana z okładzinami z płyt suchego tynku i rdzenia z papieru komórkowego-łącznie przez sklejenie).
przegrody wiotkie lub elastyczne (np. ściany z okładzinami z płyt suchego tynku i rdzenia z papieru komórkowego-łącznie przez specjalne wyprofilowanie obrzeża rdzenia).
Przegrody sztywne charakteryzują się nieco większą izolacyjnością w paśmie częstotliwości niskich, natomiast znacznie mniejszą izolacyjnością w paśmie częstotliwości średnich i wysokich. Wskaźniki izolacyjności dla tego typu przegród są więc niekorzystne.
Przegrody wiotkie charakteryzują się nieco gorszą izolacyjnością w paśmie częstotliwości niskich, za to znacznie korzystniejszymi właściwościami w paśmie częstotliwości średnich i wysokich.
Przegrody lekkie warstwowe mogą być również stosowane jako przegrody podwójne. Szczególnie korzystne właściwości uzyskuje się przy ścianach sztywnych. Wiotkie ściany podwójne wykazują niewielką izolacyjność w paśmie częstotliwości niskich, za to charakteryzują się dużą izolacyjnością w paśmie częstotliwości wysokich.
41. Właściwości akustyczne stropów
Stropy w odróżnieniu od ścian powinny charakteryzować się nie tylko odpornością na przenikanie dźwięków powietrznych, ale również tłumieniem dźwięków uderzeniowych.
Przez odpowiedni dobór konstrukcji stropu można zagwarantować spełnienie wymagań dotyczących izolacyjności od dźwięków powietrznych, nie można jednak uzyskać dostatecznej izolacji na dźwięki uderzeniowe. Od dźwięków powietrznych płyt stropowych jest różna dla płyt średnich i kanałowych. Płyty kanałowe charakteryzują się nieco korzystniejszymi wskaźnikami Rw.
Tłumienie dźwięków uderzeniowych przez płyte stropową jest uzależnione od masy stropu, grubości i konstrukcji. Dla płyt pełnych poziom uderzeniowy L pod stropem określa wyrażenie:
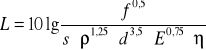
[dB]
gdzie:
s - powierzchnia stropu
d - grubość stropu
![]()
- gęstość materiału kg/m3
E - moduł sprężystości N/m2
![]()
- współczynnik strat wewnętrznych N/m2
F - częstotliwość Hz
Z wzoru wynika ,że poziom uderzeniowy w większym stopniu zależy od grubości płyty niż od gęstości oraz modułu sprężystości materiału płyty.
Stropy kanałowe ze względu na większą grubość płyty charakteryzują się niższym poziomem uderzeniowym niż strupy płytowe. najbardziej niekorzystne pod względem tłumienia dźwięków uderzeniowych.
42. Charakterystyka światła. Widmo promieniowania.
Źródła światła dzieli się na źródła naturalne i sztuczne. Światło jest rodzajem energii elektromagnetycznej promienistej wysyłanej kwantami promieniowania lub fotonami biegnącymi z prędkością 300 000km/s.
Do emisji fal elektromagnetycznych dochodzi w wyniku przejścia powstających w ten sposób fal zależy od różnicy energii w obu stanach. Długość tych fal jest związana z częstotliwością drgań fotonów.
Wszystkie fale elektromagnetyczne, mimo że różnią się od siebie długością i częstotliwością mają taką samą naturę. Razem tworzą tak zwane widmo fal elektromagnetycznych. Praktycznie nie ma granicy. Rozciąga się od częstotliwości równych 0 do nieskończoności.
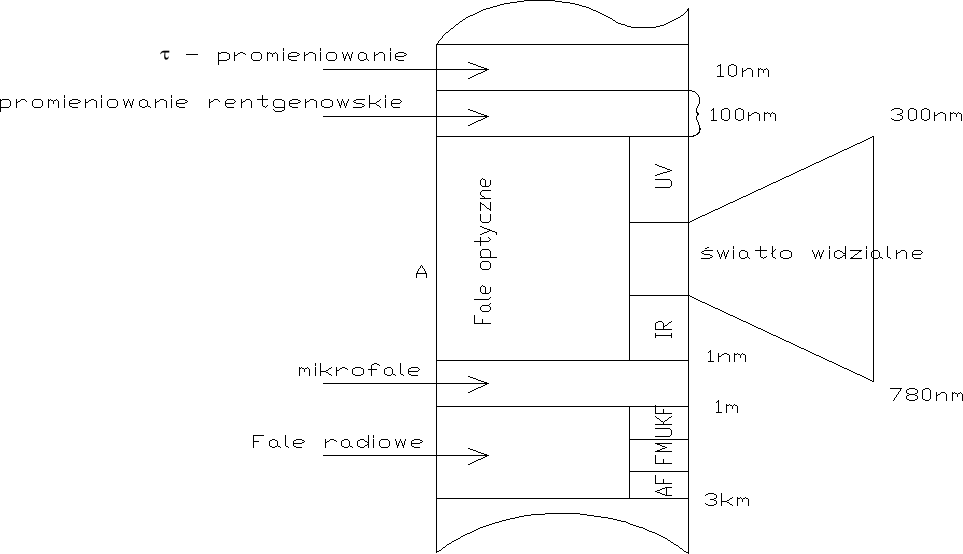
Promieniowanie optyczne jest jedynym promieniowaniem wykrywalnym przez ludzkie zmysły, za pośrednictwem specjalnych receptorów. W zakresie światła widzialnego-czopki i pręciki oka.
Promieniowanie widzialne czyli światło obejmuje zakres długości fali od 380+780mm.Jest jednym z podstawowych czynników warunkujących życie na ziemi. W zakresie promieniowania widocznego każde promieniowanie monochromatyczne( to jest, o określonej długości fali ),wywołuje wrażenie światła określonej barwy. Promieniowanie widzialne zawiera fale o wszystkich długościach. Wywołuje wrażenie tak zwanego światła białego. Każde ciało świecące w wyniku nagrzewania od wysokiej temperatury wysyła oprócz promieniowania widzialnego także promieniowanie podczerwone(IR) oraz nadfioletowe(UV).Ale promieniowanie, które jest w stanie wywołać u człowieka wrażenie wzrokowe ma długość fali z przedziału 380+780mm.Skale prażeń dla padającego promienia wytwarza oko, które odróżnia 8 podstawowych barw światła.
Rozmieszczenie ich w skali długości fal jest następujące:
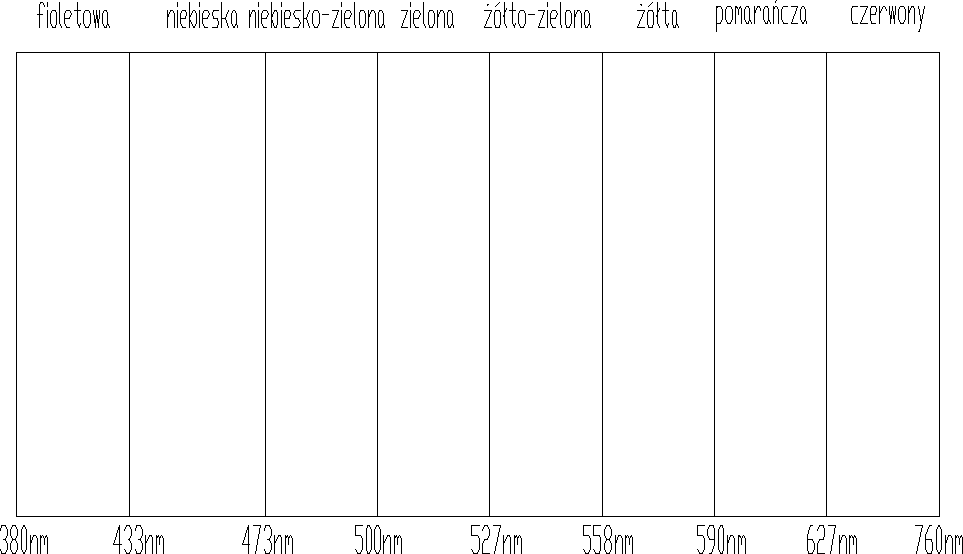
43.Wielkości świetlne promieniowana widzialnego
Do ocen promieniowania widzialnego stosuje się następujące wielkości fotometryczne: strumień świetlny (Φ), światłość (J), natężenie oświetlenia czy jasność (E), luminacja świetlna (L).
Strumień świetlny (Φ) stanowi miarę mocy świetlnej. Jednostką jest lumen (Lm) .
Światłość (J) jest ilorazem strumienia świetlnego wysyłanego przez punktowe lub powierzchniowe źródło światła i odpowiedniego kąta Ω, w którym ten strumień rozprzestrzenia się.
![]()
Jednostką światłości jest Candela [cd], którą definiuje się jako światło źródła, które w danym kierunku wysyła promieniowanie monochromatyczne.
Natężenie oświetlenia lub jasność- określa gęstość powierzchniową strumienia świetlnego padającego na pewną powierzchnię:
![]()
E, luks, (Lx), który odpowiada natężeniu oświetlania na powierzchni 1m2, na którą działa strumień świetlny wielkości 1 lumena.
Natężenie oświetlenia można też wyrazić w zależności od światłości źródła i odległości obiektu oświetleniowego od źródła.
![]()
gdzie:
I - światłość źródła punktowego
r - odległość obiektu od źródła
![]()
- kąt zawarty między kierunkami promieni a prostopadłą do powierzchni
Do opisu wrażenia wzrokowego wywieranego przez oświetlenie powierzchni służy tzw. luminacja światła, czyli stosunek światłości danej powierzchni do pozornego pola jej powierzchni, będącego rzutem tej powierzchni na płaszczyznę prostopadłą do kierunku zwrotu. Schemat biegu promieniowania świetlnego od powierzchni świecącej do oka wygląda w następujący sposób:
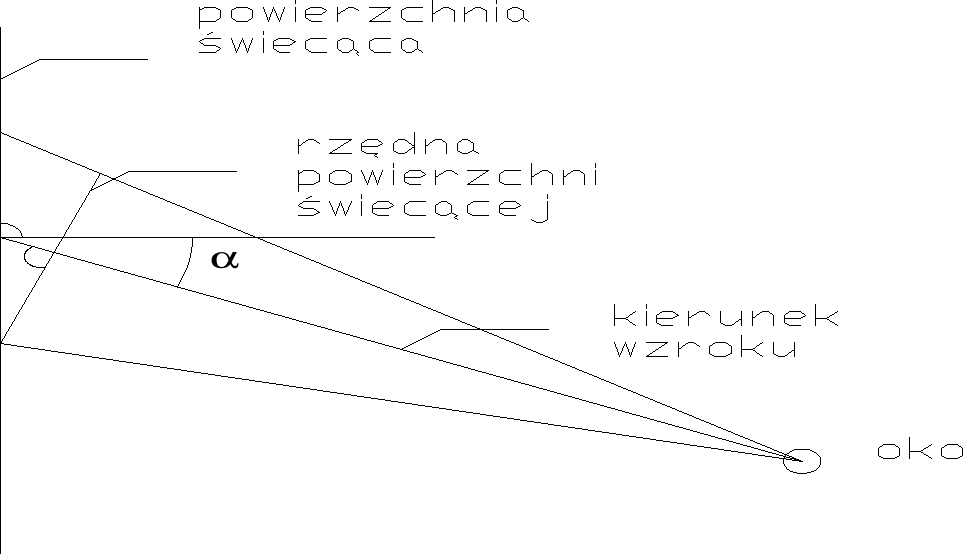
Jeżeli światłość powierzchni świecącej jest równomierna to luminacja wyraża się wzorem:
![]()
Jednostką luminacji jest nit (nt) odpowiadający luminacji powierzchni 1m2, której światłość w płaszczyźnie prostopadłej do tej powierzchni wynosi 1 kondela (cd)
![]()
Iloczyn luminacji powierzchni świecącej i rzutu na płaszczyznę oświetloną kąta przestrzennego obejmującego obejmującego z danego punktu powierzchnię świecącą odpowiada natężeniu oświetlenia w danym punkcie płaszczyzny.
![]()
gdzie:
L - luminacja powierzchni
![]()
- kąt przestrzenny
![]()
- średni kąt padania światła
Powyższą zależność nazywa się prawem rzutów kąta przestrzennego i wykorzystuje w metodach obliczeniowych natężenia oświetlenia dziennego.
Strumień świetlny padający na daną powierzchnię może być częściowo pochłonięty, odbity lub przepuszczony przez tę powierzchnię. Stosunek pochłoniętej, odbitej, przepuszczonej ilości światła do całego strumienia ![]()
określa właściwości materiału i nazywa się odpowiednio:
- współczynnikiem pochłaniania światła ![]()
- współczynnikiem odbicia światła 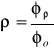
- współczynnikiem przepuszczania światła ![]()
Zgodnie z zasadą bilansu energetycznego strumień świetlny, padający na powierzchnię przegrody (![]()
) winien być równy sumie strumieni cząstkowych powstałych w wyniku jego rozdzielania na trzy części, tj.
![]()
- dzieląc obustronnie równanie przez ![]()
otrzymuje się wyrażenie określające związek między wyżej wymienionymi współczynnikami.
W technice świetlnej największe znacznie mają zjawiska odbicia i przepuszczania światła. Powierzchnie odbijające światło pełnią ważną funkcję, gdyż stanowią wtórne źródło światła poprawiając warunki oświetlenia wnętrz. Wielkość i charakter odbicia od cech geometrycznych powierzchni i jej barwy.
W przypadku powierzchni gładkich odbicie może być kierunkowe i powierzchnia wydaje się jasna, błyszcząca, w kierunku odbicia promieni, a w innym kierunku sprawia wrażenie ciemnej. W przypadku odbicia rozproszonego odbity strumień cieplny może być rozproszony we wszystkich kierunkach. Luminacja powierzchni świecących lub odbijających w sposób rozproszony nie zależy od kierunku, z którego na nią patrzy obserwator. Wydaje się, że jest ona jednakowo jasna we wszystkich kierunkach.
44. Kontrast luminacji i barw.]
Obiekt obserwowany może odróżniany od tła dzięki kontrastowi luminacji i barw. Kontrast ten wyraża się wzorem:
![]()
Lmax, min - max. i min. luminacja
Postrzeganie wzrokowe przedmiotu obserwowanego wymaga oświetlenia go do pewnego minimalnego poziomu. Przedmiot ten musi mieć duże minimalne wymiary oraz powinien w pewnym stopniu kontrastować z tłem. Aby obserwować przedmioty nie wielkie i słabo kontrastujące z tłem należy zapewniać oświetlenie o większym natężeniu.
Przy doborze odpowiednich parametrów oświetlenia ważne są nie tylko czynniki fizjologiczne, ale tez psychologiczne. Równomiernemu rozpowszechnianiu się światła w przestrzeni towarzyszy widzenie.
Wrażenia subiektywne |
Rodzaj wzmacniania przez oświetlenie |
1) wrażenie przejrzystości
2) wrażenie przestrzenności 3) wrażenie odprężenia (relaksu) 4) wrażenie prywatności lub intymności
5) wrażenie przyjemności i preferencji |
- jasne równomierne oświetlenie; pełne peryferyjne uwydatnienie - równomierne oświetlenie peryferyjne - oświetlenie nierównomierne; raczej uwydatnienie peryferyjne niż oświetlenie górne - oświetlenie nierównomierne; tendencja w kierunku niskich poziomów intensywności światła w bezpośrednim otoczeniu użytkownika oraz wyższych wartości jaskrawości dalej od użytkownika. - oświetlenie nierównomierne; uwydatnienie peryferyjne (ścian) |
Wpływ efektów oświetlenia wrażenie subiektywne człowieka jest następujące:
Wzrokowe postrzeganie barwy jest odczuciem bardzo subiektywnym. Do ścisłego określania barwy widmowo czystej wystarczy podanie długości jej fali. W przypadku barwy złożonej takie działanie nie może mieć zastosowania. Barwę złożoną ciała w świetle przechodzącym lub odbitym można określić na podstawie spektrofotometru; wyznaczając krzywą rozkładu widmowego natężenia światła w długości fali. Jest to jednak badanie dość skomplikowane i dlatego częściej stosuje się metodę teoretyczną bazującą na matematycznym zapisie barwy:
Według tej metody zostały przyjęte jako podstawowe trzy barwy widmowo czyste:
- czerwona - długość fali 700 nm
- zielona - długość fali 546 nm
- fioletowa - długość fali 435 nm
W celu określenia punktu płaszczyzny wykreśla się trójkąt równoboczny, którego wysokość przyjmuje się za jednostkę długości fali.
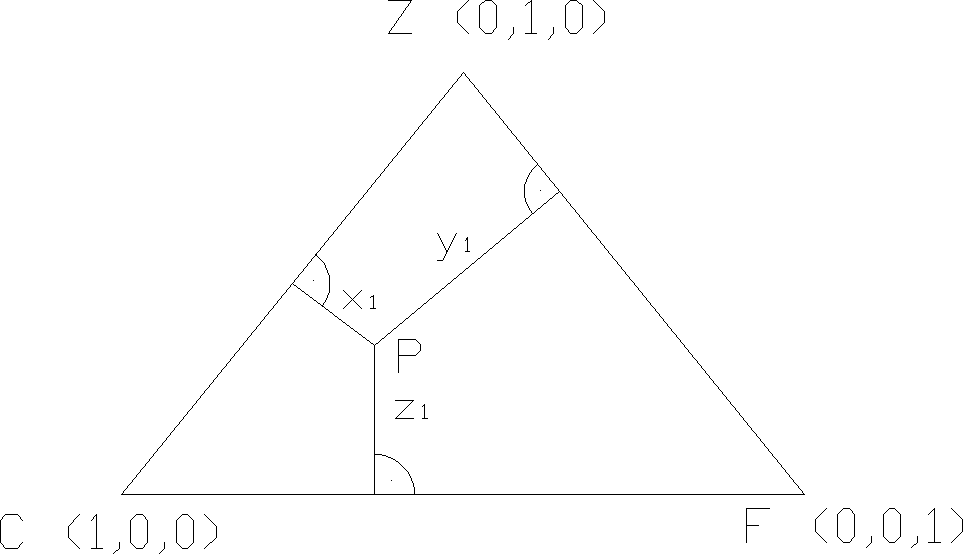
Położenie każdego punktu płaszczyzny można zdefiniować liczbami x1, y1, z1 wyrażającymi odległość tego punktu od trzech boków trójkąta.
Udział poszczególnych barw podstawowych w określonej barwie złożonej określa się wówczas w oparciu o następujące wielkości.
![]()
; ![]()
; ![]()
x1+y1+z1 = 1
45. Czynniki wpływające na oświetlenie dzienne oraz kryteria jego oceny
Ujemną cechą światła dziennego jest jego zmienność w zależności od czasu i warunków atmosferycznych co decyduje o konieczności projektowania otworów oświetleniowych według warunków niekorzystnych.
Na oświetlenie dzienne w budynkach mają wpływ czynniki niezależne od człowieka oraz takie, które człowiek może kształtować. Do czynników nie zależnych zalicza się pory roku i dnia; warunki atmosferyczne (zachmurzenia, mgła)
Czynniki zależne to:
- usytuowanie budynku w terenie
- rodzaj, położenie i wielkość otworów oświetleniowych
- otoczenie budynków ze względu na światło odbite oraz charakterystyka geometryczna powierzchni odbijającej i jej barwa.
Światło słoneczne w warunkach klimatycznych Polski operuje tylko przez 33% w roku jako światło bezpośrednie, kierunkowe i dociera do wnętrza budynku na krótko oraz oświetla bezpośrednio niewielką jego część.
Rozproszona część światła słonecznego zależy od stanu atmosfery i od zachmurzenia. Przy bezchmurnym niebie, światło rozproszone stanowi 10% całej ilości światła słonecznego, a przy pełnym zachmurzeniu 100%.
Polskie warunki klimatyczne w obliczeniach oświetleniowych, jest brane pod uwagę wyłącznie rozproszone światło nieboskłonu czyli tak zwanego stanu nieba pokrytego.
Nasłonecznienie bezpośrednie promieniowania słońca w oświetleniu wnętrz nazywa się insolacją. Insolacja stanowi czynnik dodatkowy. Z punktu widzenia warunków higienicznych insolacja jest zjawiskiem pożądanym.
W wielu przypadkach insolacja jest zjawiskiem nie pożądanym, ponieważ może być zjawiskiem olśnienia oczu, przegrzania pomieszczeń w okresie letnim. Może też destrukcyjnie oddziaływać na materiały budowlane.
Projektując otwory okienne stosuje się pojęcie charakteryzujące minimalny stosunek jasności oświetlenia wewnętrznego do występującej w danej miejscowości jasności przeciętnej, zewnętrznego oświetlenia dziennego. Stosunek ten nazywamy współczynnikiem oświetlenia dziennego i obliczmy ze wzoru:
![]()
gdzie:
Ew - natężenie światła wewnątrz pomieszczenia
Ez - natężenie światła na zewnątrz
Poza współczynnikiem światła dziennego e wykorzystuje się też wskaźnik równomierności oświetlenia dziennego w pomieszczeniu:
![]()
Wskaźnik ten jest określany w warunkach nieba pokrytego czyli zachmurzonego, przy którym mamy minimalne natężenie zewnętrzne wystarczające dla oświetlenia dziennego pomieszczenia minimalną wielkością graniczną:
Emin= 5000Lx
Emax= 50000Lx
46. Wskaźniki orientacyjne wystarczającego oświetlenia dziennego
W celu zapewnienia dostatecznego dostępu światła dziennego do najniższych kondygnacji w wytycznych urbanistycznych określono minimalną odległość między równoległymi budynkami na 1,5 wysokości wyższego budynku.
W przepisach budowlanych podano najmniejszy dopuszczalny stosunek powierzchni okna do powierzchni podłogi pomieszczenia.
Powyższe nie są wystarczające, gdyż na oświetlenie w pomieszczeniu poza wielkością okien ma wpływ ich kształt i usytuowanie nad poziomem podłogi, a także głębokość pomieszczenia i jego proporcje. Z pośród wymienionych czynników najgłówniejsze są:
wielkość otworu
głębokość pomieszczenia
Przy oświetleniu bocznym okien pomieszczeń mieszkalnych o podwójnym oszkleniu usytuowanych na wysokości 0,85 m nad podłogą i przy otwartej przestrzeni na zewnątrz przed oknami, orientacyjnie wskaźniki mogą być następujące:
Stosunek głębokości powierzchni L do wysokości okna L/h0 |
Stosunek powierzchni okna Fo do powierzchni podłogo Fp Fo/Fp |
||
|
Czynność wzrokowa |
||
|
Dokładna |
Średnio dokładna |
Zgrubna |
1,5 1,5 - 2 2 - 2,5 2,5 - 3,0 |
e = 0,2 e = 0,25 e = 0,30 niedopuszczalne |
e = 0,15 e = 0,20 e = 0,25 e = 0,30 |
e = 0,10 e = 0,15 e = 0,16 e = 0,20 |
Przy innym położeniu okien, przy górnym i mieszanym oświetleniu, a także przy uwzględnieniu światła odbitego od wewnętrznej i zewnętrznej powierzchni, stosowanie wskaźników orientacyjnych nie jest możliwe.
W tym przypadku konieczne jest określenie współczynnika oświetlenia dziennego oraz porównanie jego z wartościami normowymi.
47. Określanie współczynnika oświetlenia dziennego
Przy określeniu parametrów oświetlenia dziennego wstępnie przyjmujemy szereg otworów okiennych, wybranych wymiarów, kształtu i lokalizacji. Dla wybranego układu otworów dalej obliczmy współczynnik oświetlenia dziennego.
Wartości współczynników oświetlenia dziennego są określane w przekroju pionowym, prostopadłym do płaszczyzny otworów świetlnych przechodzącym przez środek pomieszczenia.
Współczynnik oświetlenia dziennego dla dowolnego punktu w pomieszczeniu jest sumą trzech składowych:
- składowej nieboskłonu en; od światła padającego bezpośrednio z nieboskłonu po przejściu przez oszklony otwór świetlny
- składowej odbić wewnętrznych ew; od powierzchni pomieszczenia
- składowej odbić zewnętrznych ez; od powierzchni zewnętrznych po przechodzeniu światła przez oszklony otwór świetlny
e = en + ew + ez
Wartość składowej nieboskłonu ] współczynnika oświetlenia dziennego dla światła bezpośredniego oblicza się wzorem:
![]()
gdzie:
en,o - współczynnik nieboskłonu; oblicza się metodą Daniluka czy Wienera
Metoda Daniluka - polega na wyliczeniu liczby promieni, które dopływają przez otwory okienne do wybranego punktu w pomieszczeniu. W tym celu na rzut i przekrój pomieszczenia nakładamy wykres promieni i wyliczamy odpowiednio:
n1 - liczba promieni na rzucie
n2 - liczba promieni na przekroju
![]()
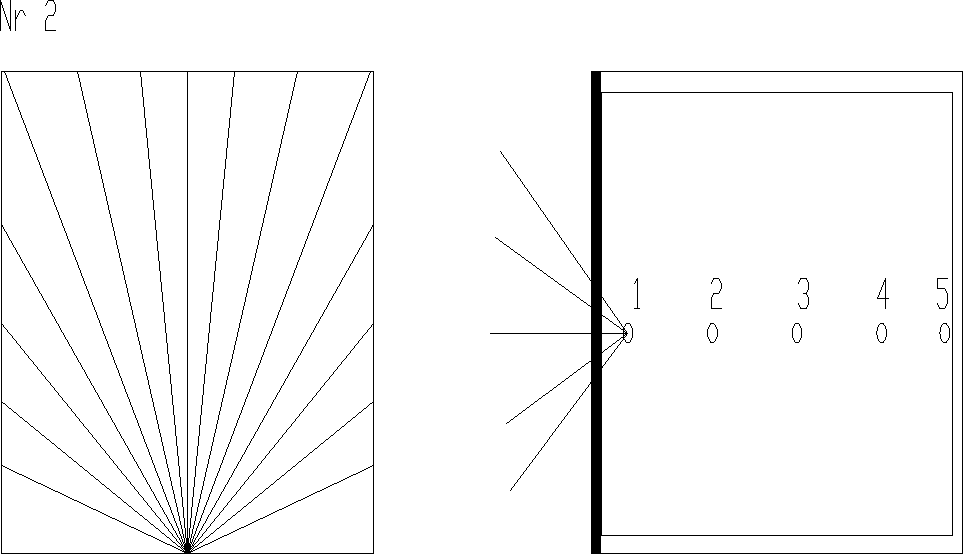
τ - współczynnik przepuszczania światła
![]()
gdzie:
![]()
- współczynniki przepuszczania światła uwzględniające odpowiednio:
τ1 - rodzaj szkła okiennego
τ2 - rodzaj oprawy okiennej
τ3 - zabrudzenie oszklenia
τ4 - uwzględnia część światła, które jest tracone (nie dopływa do pomieszczenia z powodu
konstrukcji nośnych; kratownic, belek)
q - współczynnik uwzględniający nierównomierny rozkład luminacji nieboskłony wzdłuż
południka
Składową współczynnika oświetlenia dziennego od światła odbitego od powierzchni wewnętrznych, oblicza się ze wzoru:
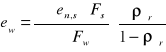
gdzie:
en,s - wartość składowej nieboskłonu współczynnika oświetlenia na wewnętrznej
powierzchni szyby
Fs - powierzchnia otworu okiennego
Fw - powierzchnia odbijająca
ρśr - średni współczynnik odbicia światła powierzchni odbijających
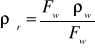
gdzie:
Fw - powierzchnia ścian, podłogi i sufitu
ρw - współczynnik odbicia światła od ścian, podłogi, sufitu
Składowa odbić zewnętrznych w dowolnym punkcie pomieszczenia wyznacza się ze wzoru:
![]()
gdzie:
en,b - wartość współczynnika nieboskłonu jaka zapewniałaby w danym punkcie
promieniowanie wycinka nieboskłonu zasłoniętego budynkami przeciwległymi
τo - współczynnik przepuszczania światła
Składowa odbić zewnętrznych (ez) uwzględnia się tylko wtedy, gdy zaciemnienie przeciwległymi budynkami zostało uwzględnione przy wyznaczaniu składowej (en).
48. Wymagania normowe oświetlenia dziennego przy projektowaniu
budynku
Oświetlenie pomieszczeń światłem dziennym należy określać wartościami współczynnika oświetlenia dziennego w szeregu charakterystyce punktów ( co najmniej 5) położonych zazwyczaj na przecięciu dwóch płaszczyzn, czyli pionowej płaszczyzny charakterystycznej przekroju pionowego pomieszczeń i umownej płaszczyzny pracy na h=0,85m nad podłogą.
W pomieszczeniach z oświetleniem bocznym dla porównania z wartościami normowymi współczynnika oświetlenia przyjmuje się wartość emin w strefie bocznej charakterystycznego przekroju pomieszczenia na odległości 0,7m od ściany wewnętrznej.
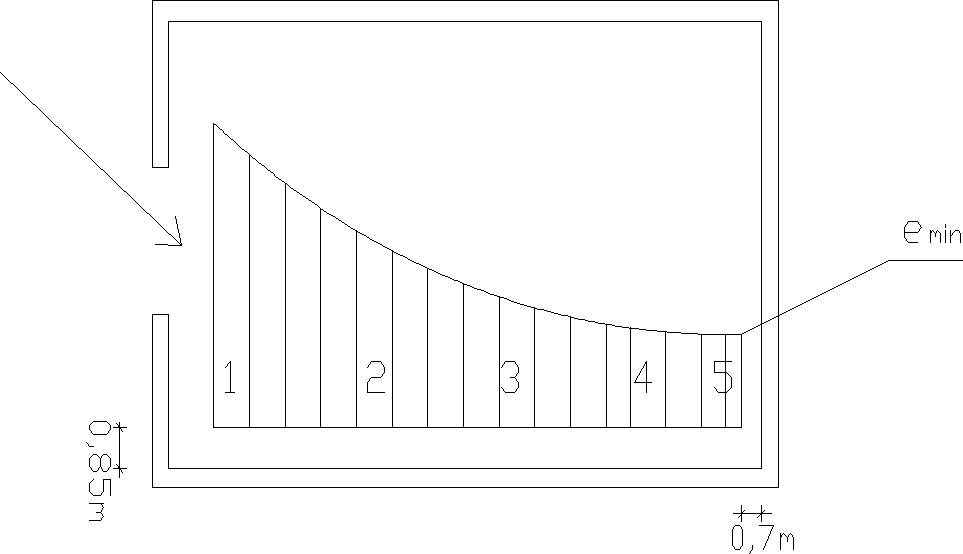
W pomieszczeniu z oświetleniem górnym lub mieszanym dla porównania z wartością normową współczynnika oświetlenia przyjmuje się wartość średnia współczynnika oświetlenia eśr , które oblicza się ze wzoru:
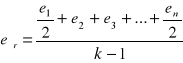
gdzie:
k - liczba punków
e1,e2,e3,…, - wartość współczynnika oświetlenia w poszczególnych punktach
Wartości liczbowe współczynnika oświetlenia dziennego nie powinny być mniejsze od wartości normowych.
emin ≥ eminn
eśr ≥ eśrn
Jeżeli powyższe warunki są niespełnione, to zwiększamy wymiary otworów okiennych i ponownie wykonujemy obliczenia współczynnika oświetlenia e.
Wartości normowe współczynnika oświetlenia dziennego zależą od kategorii czynności wzrokowych. Według Polskiej normy PN 71/B - 02380 wymagane wartości współczynnika oświetlenia dziennego są następujące:
Kategoria czynności wzrokowej |
Charakterystyczne czynności |
Wymiar charakterystyczny przedmiotu. |
eśrn |
eminn |
I II III IV V VI |
szczegółowo dokładna bardzo dokładna dokładna mało dokładna zgrubna nadzór ogólny
|
do 0,1 mm 0,1 - 0,3 mm 0,3 - 1,0 mm 1,0 - 10 mm >10 mm - |
10% 7% 5% 3% 2% 1% |
3,5 - 4 2 - 3 1,5 - 2 1 - 1,2 0,5 - 0,8 0,3 |
W pomieszczeniach o dużej głębi, w których strefy robocze są oświetlone niedostatecznie światłem dziennym, dopuszcza się kombinowane oświetlenie (dzienne + elektryczne), zapewniając przy tym warunki oświetlenia zgodnie z wymaganiami normy.
1
21