Analiza współzależności
Analiza współzależności ma na celu odkrycie i opisanie zależności jakie zachodzą pomiędzy cechami w pobranej próbie oraz w populacji.
Korelacja
Korelacja Pearsona
Korelacja Pearsona to miara współzależności, która może być stosowana wyłącznie dla danych ilościowych (cech ilościowych).
Kowariancja
Dla szeregów szczegółowych:
![]()
gdzie n to ilość badanych obserwacji, xi i yi - i-te wartości badanych cech, x i y z kreską - średnie arytmetyczne cechy X i Y.
Dla szeregów rozdzielczych (zapisanych w postaci tablicy korelacyjnej):
![]()
gdzie nij jest ilością obserwacji odpowiadającą i-tej wartości cechy X i j-tej wartości cechy Y.
Kowariancja zawsze znajduje się w przedziale:
![]()
Interpretacja: Wartości dodatnie kowariancji oznaczają zależność dodatnią (jednoczesny wzrost lub spadek wartości obydwu cech), wartości ujemne oznaczają zależność ujemną (jednoczesny wzrost wartości jednej z cech i spadek wartości drugiej).
Korelacja
![]()
gdzie sX i sY są odchyleniami standardowymi cechy X i cechy Y.
Korelacja znajduje się zawsze w przedziale:
![]()
Interpretacja: Wartości korelacji blisko 0 oznaczają brak zależności, wartości bliskie 1 lub -1 oznaczają występowanie silnej liniowej lub prawie liniowej zależności. Wartości dodatnie oznaczają zależność dodatnią (jednoczesny wzrost lub spadek wartości obydwu cech), wartości ujemne oznaczają zależność ujemną (jednoczesny wzrost wartości jednej z cech i spadek wartości drugiej).
Korelacja rang Spearmana
Korelacja rang Spearmana jest miarą współzależności, którą stosuje się dla danych porządkowych, tzn. danych ilościowych oraz danych jakościowych zawierających naturalny porządek.
Ranga to kolejny numer w uporządkowanym szeregu wartości cechy.
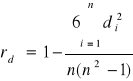
gdzie n jest ilością obserwacji, di - różnicą pomiędzy rangami obliczanymi oddzielnie dla obydwu cech.
Interpretacja: Interpretacja jest taka sama jak w przypadku korelacji Pearsona.
Dla cech jakościowych nie posiadających naturalnego porządku do badania współzależności stosuje się testy nieparametryczne, np. test niezależności 2.
Regresja
Regresja to prosta, krzywa lub łamana opisująca w sposób najdokładniejszy zależność korelacyjną pomiędzy cechami.
Regresja I rodzaju
Funkcja regresji I rodzaju zmiennej losowej X względem zmiennej losowej Y.
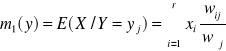
Funkcja regresji I rodzaju zmiennej losowej Y względem zmiennej losowej X.
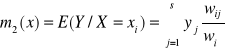
gdzie w jest odpowiednią częstością obserwacji.
Regresja I rodzaju jest łamaną łączącą punkty o współrzędnych (m1(yj), yj) lub (xi, m2(xi)).
Regresja II rodzaju
Regresja II rodzaju to prosta najlepiej wpasowana pomiędzy punkty na wykresie korelacyjnym. Jest prostą najlepiej opisującą zależność korelacyjną.
Zależność zmiennej od zmiennej X opisana jest wzorem:
![]()
gdzie
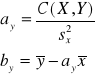
Wyszukiwarka
Podobne podstrony:
Badanie zale no ci oporu, Mateusz 24
Wyznacznie zale no ci podat
Ebsco Cepuch & Wordliczek Ocena zale no ci pomi dzy nat eniem bólu a wyst powaniem l ku i depresji
Wyznaczanie wspó czynnika lepko ci cieczy metod Ostwalda, Pracownia Zak˙adu Fizyki Technicznej Polit
Analiza funkcji dyskryminacyjnej - Opis, Psychologia, Statystyka, psychometria
KOLOKWIUM Z ANALIZY STRUKTURY TEMAT YY 2004, Statystyka Opisowa UG
KOLOKWIUM Z ANALIZY STRUKTURY TEMAT B1 2005, Statystyka Opisowa UG
KOLOKWIUM Z ANALIZY STRUKTURY TEMAT C1 2005, Statystyka Opisowa UG
KOLOKWIUM Z ANALIZY STRUKTURY TEMAT D1 2005, Statystyka Opisowa UG
KOLOKWIUM Z ANALIZY STRUKTURY DB (skrócony0 2008, Statystyka Opisowa UG
KOLOKWIUM Z ANALIZY STRUKTURY TEMAT A1 2005, Statystyka Opisowa UG
Analiza regresji między dwiema zmiennymi, Statystyka, statystyka(3)
ANALIZA STRUKTURY ROZKŁADU JEDNOWYMIAROWEGO(2), SGH, statystyka
Analiza regresji między dwiema zmiennymi, statystyka matematyczna(1)
Pomiary wspó czynnika stratno ci dielektryków za pomoc mier, Z miernika dobroci zamieszczonego na ry
Analiza struktur, Płyta farmacja Bydgoszcz, statystyka, pozostałe
więcej podobnych podstron