POLTECHNIKA WARSZAWSKA

WYDZIAŁ INŻYNIERII ŚRODOWISKA

PROJEKT SIECI I OBIEKTÓW WODOCIĄGOWYCH

Prowadząca: dr inż. Elżbieta Osuch-Pajdzińska

Wykonał: Michał Krysiak

Grupa: ISIW 1

1. Obliczenie charakterystycznego wskaźnika zużycia wody.

Zadanie polega na obliczeniu charakterystycznych wielkości zapotrzebowania na wodę dla miasta, które w okresie perspektywicznym będzie liczyło 35 000 mieszkańców. Miasto będzie posiadało zabudowę wielorodzinną wysoką, wielorodzinną niską oraz jednorodzinną.

Mieszkania w mieście będą wyposażone w wodociąg, kanalizację, wc oraz łazienkę z centralnym doprowadzeniem ciepłej wody.

Sprzedaż wody w mieście kształtowała się w ostatnich pięciu latach na poziomie przedstawionym w tabeli.

Sprzedaż wody w mieście (dane z Urzędu Gminy):

Sprzedaż wody w mieście
Rok	Liczba mieszkańców w mieście	Liczba mieszkańców korzystających z wodociągu w mieszkaniu w % ogólnej liczby mieszkańców	Sprzedaż wody w mieście tys.m^3/rok dla
						gospodarstw domowych	przemysłu	innych odbiorców
2005	23 700	75	1 112,0	178,3	184,2
2006	26 544	78	1 227,1	179,3	185,2
2007	28 668	80	1 291,3	183,9	190,0
2008	30 101	82	1 334,2	181,5	187,6
2009	31 907	85	1 440,6	177,5	183,4

W celu obliczenia jednostkowego wskaźnika ilości wody skorzystano z następujących wzorów, a wyniki zamieszczono w tabeli.

— Wskaźnik zużycia wody (ogólny wzór)
,

— Wskaźnik zużycia wody w gospodarstwach domowych
,

— Wskaźnik zużycia wody w przemyśle
,

— Wskaźnik zużycia wody w innych obiektach
.

Jednostkowe wskaźniki zużycia wody:

Jednostkowe wskaźniki zużycia wody w mieście dla lat 2005 - 2009
Rok	qM (gosp. domowe)	qP (przemysł)	qinni (innych odbiorców)
		[m^3/dM]	[m^3/dM]	[m^3/dM]
2005	0,171	0,021	0,021
2006	0,162	0,019	0,019
2007	0,154	0,018	0,018
2008	0,148	0,017	0,017
2009	0,146	0,015	0,016

W celu obliczenia charakterystycznego zapotrzebowania na wodę skorzystano z następujących wzorów:

— Średnie dobowe zapotrzebowanie na wodę
,

— Maksymalne dobowe zapotrzebowanie na wodę
,

— Maksymalne godzinne zapotrzebowanie na wodę
.

Wskaźnik jednostkowego zapotrzebowania na wodę został wybrany na podstawie przewidywań własnych związanych z rozwojem miasta, tj:

- dla zabudowy wielorodzinnej wysokiej przyjęto 0,135 m³/(M·d), ponieważ wyposażenie łazienek sprzyja większemu zużyciu wody oraz w mniejszych mieszkaniach nie przewiduje się zajmowania miejsca przez dodatkowe urządzenia (np. zmywarki), które są w stanie zmniejszyć zużycie wody w porównaniu ze zwykłym użytkowaniem mieszkania

- dla zabudowy wielorodzinnej niskiej przyjęto 0,100 m³/(M·d), ponieważ założono, że niska zabudowa jest nowsza, a mieszkania większe, stąd też znajdzie się miejsce dla dodatkowych urządzeń pozwalających zmniejszyć zapotrzebowanie dzienne na wodę.

- dla zabudowy jednorodzinnej przyjęto 0,120 m³/(M·d), ponieważ w nowo budowanych domkach istnieje możliwość zastosowania ekonomicznych urządzeń, oszczędzających wodę.

- dla usług i innych odbiorców przyjęto 0,015 m³/(M·d), ponieważ miasto rozwija się, przez co pojawia się więcej punktów usługowych, lecz wzrastająca liczba mieszkańców powoduje, że jednostkowe zużycie wody w celach usługowych na jednego mieszkańca maleje.

- dla przemysłu przyjęto 0,015 m³/(M·d), ponieważ wraz z rozwojem miasta, wprowadza się nowe technologie, które pozwalają ograniczyć zużycie wody oraz wielokrotnie wykorzystać tę samą wodę w celach przemysłowych.

Współczynniki nierównomierności dobowej i godzinowej dobrano na podstawie tabeli:

Odbiorcy wody	Współczynnik nierównomierności dobowej Nd	Współczynnik nierównomierności godzinowej Nh
Mieszkalnictwo
wielorodzinne	1,3 ÷ 1,5	1,4 ÷ 1,6
jednorodzinne	1,5 ÷ 2,0	2,5 ÷ 3,0
Usługi i inni odbiorcy	1,3	2,8 ÷ 3,0
Przemysł	1,15 ÷ 1,20	1,25 ÷ 1,50

Niektórzy odbiorcy są przedstawieni w postaci przedziału liczbowego zależnego od liczby mieszkańców, im większa liczba mieszkańców tym mniejsza wartość współczynnika, natomiast im mniejsza liczba mieszkańców tym większa wartość współczynnika.

Współczynniki nierównomierności dobowej i godzinowej dotyczą poszczególnych celów, na które zużywana jest woda na terenie objętym zasięgiem wodociągu. Ich wartości podane są według : „Wytycznych prognozowania zapotrzebowania wody i ilości ścieków w jednostkach osadniczych”.

Obliczenie charakterystycznych wielkości zapotrzebowania na wodę dla miasta, które w perspektywie osiągnie liczbę 35 000 mieszkańców.

Grupa odbiorców		Liczba mieszkańców	Wskaźnik jednostkowego zapotrzebowania na wodę		Średnie dobowe zapotrzebowanie na wodę Qd,śr	Współczynnik nierównomierności dobowej Nd	Maksymalne dobowe zapotrzebowanie na wodę Qd,max	Współczynnik nierównomierności godzinowej Nh	Maksymalne godzinowe zapotrzebowanie na wodę Qh,max	Zapotrzebowanie na wodę w godzinach maksymalnego rozbioru wody w mieście Qh,max
						Jednostka	wartość	[m^3/d]	[-]	[m^3/d]	[-]	[m^3/h]	[m^3/h]	[l/s]
1.	Mieszkalnictwo	35 000	l/Mk*d
zabudowa wysoka		17 500		135	2 363	1,4	3 308	1,5	207	206,4	57,3
zabudowa niska		3 500		100	350	1,4	490	1,5	31	30,6	8,5
zabudowa jednorodzinna		14 000		120	1 680	1,7	2 856	2,7	321	320,7	89,1
2.	Usługi i inni odbiorcy	35 000	l/M*d	15	525	1,3	683	2,9	82	20,5	5,7
3.	Przemysł	35 000	l/M*d	15	525	1,2	630	1,8	47	29,4	8,2
4.	Ogółem	35 000		-	5 443	-	7 966	-	688	-	-
5.	Straty wody 10% Qd, śr^*	-		-	544	1	544	1	23	22,7	6,3
6.	Razem	-		-	5 987	-	8 510	-	711	630,2	175,1
7.	Cele technologiczne 5% Qd, śr^*	-		-	300	1	300	1	12
	Całkowita ilość wody	-		-	6 286	-	8 810	-	724

W mieście przedstawionym w zadaniu liczba mieszkańców rośnie, a co za tym idzie, współczynniki są mniejsze. Tak więc dla miasta liczącego 35 000 mieszkańców dobrano następujące współczynniki :

Mieszkalnictwo wielorodzinne wysokie i niskie

Mieszkalnictwo jednorodzinne

Usługi i inni odbiorcy

Przemysł

Maksymalny współczynnik godzinowy obliczono ze wzoru:
.

Obliczenie maksymalnego godzinnego zapotrzebowania na wodę dla miasta, które osiągnie 35 000 mieszkańców.

Godziny	Zapotrzebowanie na wodę w poszczególnych godzinach doby przez różne grupy odbiorców
		mieszkalnictwo wielorodzinne niskie		mieszkalnictwo wielorodzinne wysokie		mieszkalnictwo jednorodzinne		usługi		przemysł		straty		razem dla miasta
		%Qd, max	m^3/h	% Qd, max	m^3/h	% Qd, max	m^3/h	% Qd, max	m^3/h	% Qd, max	m^3/h	% Qd, max	m^3/h	% Qd, max	m^3/h
0-1	1,3	6,4	1,3	43,0	1	28,6	0,5	3,4	1,4	8,8	4,17	22,7	1,33	112,9
1-2	1,2	5,9	1,2	39,7	0,3	8,6	0,5	3,4	1,4	8,8	4,17	22,7	1,05	89,1
2-3	1,1	5,4	1	33,1	0,4	11,4	1	6,8	1,5	9,5	4,16	22,6	1,04	88,8
3-4	1,2	5,9	1,2	39,7	0,8	22,8	1	6,8	1,5	9,5	4,17	22,7	1,26	107,4
4-5	2,2	10,8	2	66,2	1,1	31,4	1	6,8	1,6	10,1	4,17	22,7	1,74	147,9
5-6	4	19,6	4	132,3	3,1	88,5	1	6,8	2,3	14,5	4,16	22,6	3,34	284,4
6-7	5	24,5	5	165,4	4,4	125,7	2	13,7	3,4	21,4	4,17	22,7	4,39	373,3
7-8	5,8	28,4	6	198,5	5,5	157,1	3	20,5	4,4	27,7	4,17	22,7	5,34	454,8
8-9	5,9	28,9	5,8	191,8	4,9	139,9	5	34,1	6,24	39,3	4,16	22,6	5,37	456,8
9-10	5,1	25,0	5,2	172,0	4,9	139,9	8	54,6	6,24	39,3	4,17	22,7	5,33	453,5
10-11	5,1	25,0	5,2	172,0	3,5	100,0	9	61,4	7,4	46,6	4,17	22,7	5,03	427,7
11-12	5,2	25,5	5,2	172,0	3,5	100,0	11	75,1	7,4	46,6	4,16	22,6	5,19	441,8
12-13	5,3	26,0	5,2	172,0	3,9	111,4	12	81,9	6,7	42,2	4,17	22,7	5,36	456,1
13-14	5,4	26,5	5,3	175,3	4,5	128,5	12	81,9	6,44	40,6	4,17	22,7	5,59	475,4
14-15	5,5	27,0	5,3	175,3	6	171,4	11	75,1	5,76	36,3	4,16	22,6	5,96	507,6
15-16	5,8	28,4	5,8	191,8	7	199,9	7	47,8	5,76	36,3	4,17	22,7	6,19	526,9
16-17	5,8	28,4	5,9	195,1	7,25	207,1	3	20,5	4,76	30,0	4,16	22,6	5,92	503,7
17-18	6,24	30,6	6,24	206,4	11,23	320,7	3	20,5	4,66	29,4	4,17	22,7	7,41	630,2
18-19	5,3	26,0	5,5	181,9	7	199,9	3	20,5	4,76	30,0	4,17	22,7	5,65	481,0
19-20	5,29	25,9	5,29	175,0	6	171,4	2,5	17,1	4,86	30,6	4,16	22,6	5,20	442,6
20-21	4,17	20,4	4,17	137,9	5	142,8	1	6,8	4,76	30,0	4,17	22,7	4,24	360,7
21-22	3,52	17,2	3,52	116,4	5	142,8	1	6,8	3,76	23,7	4,17	22,7	3,87	329,7
22-23	2,38	11,7	2,48	82,0	1,22	34,8	1	6,8	1,5	9,5	4,16	22,6	1,97	167,4
23-24	2,2	10,8	2,2	72,8	2,5	71,4	0,5	3,4	1,5	9,5	4,17	22,7	2,24	190,5
	100	490,0	100	3307,5	100	2856,0	100	682,5	100	630,0	100	544,3	100,00	8510,3

2. Obliczenie pojemności wyrównawczej i wymiarów zbiornika sieciowego.

Zbiorniki w systemach wodociągowych stosowane są w celu zapewnienia ciągłości dostaw wody do poszczególnych elementów systemu, umożliwienia racjonalnego działania tych elementów oraz stworzenia rezerwy wody pozwalającej na nieprzerwanie dostaw wody do odbiorców. Zbiorniki te gromadzą wodę w godzinach małych rozbiorów, a następnie uzupełniają niedobory w okresie dużego zapotrzebowania. W zbiornikach może być także gromadzona woda na cele przeciwpożarowe.

Zadanie polega na obliczeniu wymaganej pojemności wyrównawczej i wymiary zbiornika sieciowego dla wodociągu o maksymalnej dobowej wydajności i rozkładzie godzinowego rozbioru wody w dobie maksymalnego zapotrzebowania wody.

założono: V_a = 15 %,

V_ppoż = 10 m³ na każdy 1 l/s poniżej 40 l/s wydajności wodociągu przy liczbie mieszkańców równej 25 001 ÷ 100 000 — wodociąg ma ponad 150 l/s wydajności, stąd V_ppoż = 0 m³.

Metoda analityczna:

Polega na ustaleniu odpowiedniego trybu pracy pomp. Do wykonania obliczeń przyjęto równomierną pracę pomp. Aby obliczyć wydajność godzinową pompy skorzystano ze wzoru:

Aby obliczyć maksymalną ilość wody jaką ma pomieścić zbiornik zsumowano ilość wody napływającej do zbiornika w godzinach pomniejszonego zapotrzebowania wody w mieście. Największą pojemność zbiornika uzyskano w przedziale godzinowym 6 - 7 i wyniosła ona 19,42 % Q_d,max.

W celu obliczenia pojemności wyrównawczej skorzystano ze wzoru:

Ostatecznie uzyskano wynik:

W celu obliczenia wymiarów zbiornika przeprowadzono następujące obliczenia:

Obliczenie pojemności wyrównawczej zbiornika sieciowego przy równomiernej pracy pomp.

Godziny	Wydajność pomp [% Q d max]	Zużycie wody przez miasto [% Q d max]	Przybyło do zbiornika [% Q d max]	Ubyło ze zbiornika [% Q d max]	Jest w zbiorniku [% Q d max]
24 - 1	4,17	1,35	2,82	-	4,30
1 - 2	4,17	1,07	3,10	-	7,12
2 - 3	4,16	1,02	3,10	-	10,22
3 - 4	4,17	1,27	2,90	-	13,33
4 - 5	4,17	1,75	2,42	-	16,22
5 - 6	4,16	3,38	0,78	-	18,64
6 - 7	4,17	4,43	-	0,26	19,42
7 - 8	4,17	5,38	-	1,21	19,16
8 - 9	4,16	5,40	-	1,24	17,95
9 - 11	4,17	5,28	-	1,11	16,71
10 - 11	4,17	4,98	-	0,81	15,60
11 - 12	4,16	5,09	-	0,93	14,79
12 - 13	4,17	5,22	-	1,05	13,86
13 - 14	4,17	5,44	-	1,27	12,82
14 - 15	4,16	5,82	-	1,66	11,55
15 - 16	4,17	6,16	-	1,99	9,89
16 - 17	4,17	5,97	-	1,80	7,90
17 - 18	4,16	7,46	-	3,30	6,10
18 - 19	4,17	5,70	-	1,53	2,80
19 - 20	4,17	5,26	-	1,09	1,27
20 - 21	4,16	4,34	-	0,18	0,18
21 - 22	4,17	3,95	0,22	-	0,00
22 - 23	4,17	1,98	2,19	-	0,22
23 - 24	4,16	2,27	1,89	-	2,41
	100			max	19,42

Metoda graficzna:

Metoda ta polega na wykreśleniu krzywej sumowej, która określa pojemność wyrównawczą zbiornika. Na tym samym układzie współrzędnych odkłada się sumarycznie ilości wody dostarczanej przez pompy w każdej godzinie, licząc od początku doby. Naniesione punkty po połączeniu dają rosnącą krzywą sumową w przedziale od 0 do 100% Q_d,max w godzinach 

0 - 24. Obliczeń dokonujemy zakładając 16-godzinna pracę pomp. Przez pozostałe 8 godzin pompy nie pracują, co powoduje, że stała wydajność pracy pomp wynosi 6,25 %Q_{d max}

W celu wyznaczenia pojemności zbiornika należy przesunąć wykres pracy pompy równolegle, tak aby był on styczny do wykresu krzywej sumowej rozbiorów. Następnie należy określić największą różnicę rzędnych pomiędzy wykresami. Odczytana różnica jest jednocześnie niezbędną pojemnością zbiornika wyrównawczego wyrażoną w % Q_d,max.

Wynik otrzymany tą metodą jest równoważny z tym, który otrzymano przy wykorzystaniu metody analitycznej.

Godziny	Wydajność pomp [% Q d max]	Zużycie wody przez miasto [% Q d max]	Przybyło do zbiornika [% Q d max]	Ubyło ze zbiornika [% Q d max]	Jest w zbiorniku [% Q d max]
24 - 1		1,33		1,33	5,09
1 - 2		1,05		1,05	4,04
2 - 3		1,04		1,04	3,00
3 - 4		1,26		1,26	1,74
4 - 5		1,74		1,74	0,00
5 - 6	6,25	3,34	2,91		2,91
6 - 7	6,25	4,39	1,86		4,77
7 - 8	6,25	5,34	0,91		5,68
8 - 9	6,25	5,37	0,88		6,56
9 - 11	6,25	5,33	0,92		7,48
10 - 11	6,25	5,03	1,22		8,71
11 - 12	6,25	5,19	1,06		9,76
12 - 13	6,25	5,36	0,89		10,65
13 - 14	6,25	5,59	0,66		11,32
14 - 15	6,25	5,96	0,29		11,60
15 - 16	6,25	6,19	0,06		11,66
16 - 17	6,25	5,92	0,33		11,99
17 - 18	6,25	7,41		1,16	10,84
18 - 19	6,25	5,65	0,60		11,43
19 - 20	6,25	5,20	1,05		12,48
20 - 21	6,25	4,24	2,01		14,50
21 - 22		3,87		3,87	10,62
22 - 23		1,97		1,97	8,66
23 - 24		2,24		2,24	6,42

3. Plan zagospodarowania przestrzennego jednostki osadniczej.

Plan zagospodarowania przestrzennego, na którym wyodrębniono tereny z istniejącym rodzajem zabudowy lub przeznaczeniem pod daną zabudowę. W danym ćwiczeniu Zaprojektowano plan zagospodarowania przestrzennego oraz lokalizację elementów systemu wodociągowego: ujęcia wody, stacji uzdatniania wody z pompownią II stopnia, zbiornik wyrównawczy, układ sieci wodociągowej magistralnej i rozbiorczej.

Zbiornik (końcowy) wyrównawczy zostanie zlokalizowany w najwyższym punkcie terenu. Pompownia II stopnia będzie usytuowana na obszarze stacji uzdatniania wody.

Projektując układ sieci wodociągowej, zaplanowano wykonanie z przewodów magistralnych dwóch zamkniętych pierścieni, co zwiększa niezawodność pracy całego układu.

Bilans powierzchni:

zabudowa wielorodzinna wysoka (ZW) - 25,25 ha

zabudowa wielorodzinna niska (ZN) - 21,53 ha

zabudowa jednorodzinna (ZJ) - 31,89 ha

tereny przemysłowe (P) - 24,18 ha

tereny usługowe (U) - 16,72 ha

powierzchnia całego miasta - 119,57 ha

4. Schematy obliczeniowe oraz obliczenia zaprojektowanej sieci wodociągowej.

W tym zadaniu należy obliczyć zapotrzebowanie mieszkańców, usług oraz przemysłu na wodę. Do obliczeń wykorzystałem dane z ćwiczenia pierwszego, a także plan zagospodarowania przestrzennego wykonany w ćwiczeniu trzecim.

Zapotrzebowanie w godzinie maksymalnego rozbioru wody przez miasto Q_h,max

Grupa odbiorców	m^3/h	l/s
zabudowa wysoka	206,4	57,33
zabudowa niska	30,6	8,50
zabudowa jednorodzinna	320,7	89,08
usługi	20,5	5,69
przemysł	29,4	8,17

W celu obliczenia współczynników cząstkowych dla poszczególnych celów zapotrzebowania na wodę skorzystano z następujących wzorów:

Zapotrzebowanie mieszkańców na obszarze zabudowy wysokiej:

Zapotrzebowanie mieszkańców na obszarze zabudowy niskiej:

Zapotrzebowanie mieszkańców na obszarze zabudowy jednorodzinnej:

Zapotrzebowanie przemysłu:

Zapotrzebowanie usług:

Mając podział powierzchni miasta ze względu na rodzaj zabudowy oraz współczynniki jednostkowego zapotrzebowania na wodę dla poszczególnych typów zabudowy można wyznaczyć rozbiory odcinkowe i węzłowe w godzinie maksymalnego zużycia wody przez miasto. Mając na uwadze założenie, że wszystkie przewody są przewodami równomiernie wydatkującymi na całej ich długości.

W tym celu skorzystano ze wzoru:

,

gdzie:

Q - rozbiór wody [l/s]

q_i - wskaźnik jednostkowego zapotrzebowania na wodę dla i - tej powierzchni, cząstkowej

przyporządkowanej danemu odcinkowi [l/s·ha]

F_i - wielkość i-tej powierzchni cząstkowej przyporządkowanej danemu odcinkowi

(z podziału powierzchni) [ha],

n - liczba powierzchni cząstkowych przyporządkowanych danemu odcinkowi.

W celu wyznaczenia rozbiorów w godzinie minimalnego zapotrzebowania na wodę przez miasto, należało otrzymane rozbiory maksymalne przemnożyć przez współczynnik rozbiorów minimalnych A otrzymany ze wzoru:

Natomiast aby otrzymać rozbiory w godzinie maksymalnego zapotrzebowania na wodę przez miasto oraz panujących w tym samym czasie pożarów, należało otrzymane rozbiory maksymalne przemnożyć przez współczynnik pożarowy B otrzymany ze wzoru:

Ponadto wyznaczono kierunki przepływów na magistrali oraz ustalono położenie węzłów zerowych, gdzie spotykają się strumienie wody płynące z różnych kierunków. Po wyliczeniu oraz późniejszym zsumowaniu obliczonych rozbiorów odcinkowych otrzymano wyjściowe wartości zapotrzebowania na wodę przez miasto. Oznacza to, że obliczenia były poprawnie wykonane i można przystąpić do dalszych prac. Następnym krokiem było wyznaczenie przepływów początkowych oraz końcowych projektowanej sieci wodociągowej.

Przepływy początkowe obliczono ze wzoru:

Przepływy końcowe obliczono ze wzoru:

• Dla przepływów maksymalnych:

• Dla przepływów minimalnych:

• Dla sytuacji pożarowej:

Obliczenia hydrauliczne sieci zostały przeprowadzone, w oparciu o wcześniej otrzymane wartości przepływów oraz rozbiorów odcinkowych.

Średnicę, prędkość oraz jednostkowy spadek ciśnienia dla danego przepływu obliczeniowego odczytujemy z nomogramu do obliczania strat hydraulicznych i natężenia przepływu w rurach żeliwnych i stalowych według Colebrooka i White'a.

Żeby odczytać te wartości należy początkowo założyć prędkość v = 1m/s. Wówczas dla tej prędkości i przepływu obliczeniowego dobieramy średnicę (najmniejsza możliwa równa jest 100 mm) i dla tej średnicy oraz przepływu odczytujemy spadek oraz prędkość.

Średnica przewodu wodociągowego policzono ze wzoru:

[mm]

Gdzie:

Q - natężenie przepływu wody, m³/s

v- średnia prędkość przepływu wody w przewodzie, m/s

Średnia prędkość przepływu wody jest wartością zakładaną, od 0,5 do 2,0 m/s.

Zalecana jest prędkość nie większa niż 1,0 m/s.

Całkowite straty ciśnienia przy przepływie wody w przewodach są wynikiem tarcia wewnętrznego cząstek wody (lepkości) i tarcia wody o ścianki przewodu (chropowatość) są to straty liniowe oznaczane jako h_l oraz straty miejscowe h_m, z czego wynika suma strat:

H = h_l + h_m [m]

Wysokość strat ciśnienia obliczono na odcinku przewodu o stałej średnicy i danej długości stosuje się wzór Darcy'ego i Weisbacha:

h_l=
[m]

gdzie:

l-długość odcinka przewodu, m

-współczynnik oporów liniowych, bezwymiarowych

h_l - wysokość strat liniowych, m

g - przyśpieszenie ziemskie, m/s²

v- średnia prędkość przepływu wody w przewodzie, m/s

Jednostkową stratę ciśnienia na odcinku przewodu oblicza się według wzoru:

i = h_l/l [%_o]

Po przekształceniu możemy otrzymać:

i = 0,0827
[%_o]

Współczynnik oporów liniowych
wyznacza się ze wzoru Colebrooka i White'a

Gdzie:

k- chropowatość przewodu, m

d- średnica przewodu, m

Re- liczba Reynoldsa, bezwymiarowe

Liczba Reynoldsa wyraża się wzorem:

Re =
[-]

Gdzie:

d- średnica przewodu, m

v- średnia prędkość przepływu wody w przewodzie, m/s

V- współczynnik lepkości kinetycznej wody zależny od temperatury.

Korygowanie przepływów wykonano metodą Crossa. Podstawę tej metody stanowią dwa warunki:

• Suma dopływów w węźle powinna być równa sumie odpływów z każdego węzła,

• Algebraiczna suma strat ciśnienia w każdym pierścieniu powinna być równa 0.

Metoda ta polega na kolejnych przybliżeniach. Przepływy są korygowane w sposób, iż w kolejnych przybliżeniach do przepływu poprzedniego dodawana jest poprawka obliczona ze wzoru:

gdzie:

h_i - suma wysokości strat ciśnienia na wszystkich odcinkach pierścienia w m

Q_i - przepływ obliczeniowy w i-tym odcinku pierścienia w m.

Wymagania dotyczące średnic, prędkości i materiału przewodów sieci wodociągowej średnice przewodów sieci wodociągowej powinny być korzystne zarówno pod względem technicznym, jak i ekonomicznym. Przy obliczaniu hydraulicznym sieci miano na uwadze oprócz stabilności hydraulicznej również jej koszty inwestycyjne i eksploatacyjne. Zgodnie z zaleceniami polskiej normy, najmniejsze średnice przewodów sieci miejskiej przyjęto 100 mm. Średnia prędkość przepływu wody v jest wielkością założoną w procesie projektowania przewodów i waha się w okolicach 1 m/s.

Wartość ta wynika z warunków ekonomicznych i eksploatacyjnych sieci wodociągowej. Przy określaniu prędkości w przewodach kierowano się zaleceniem polskiej normy

PN-76/M-34034-Rurociągi. Zasady obliczeń strat ciśnienia.

W projekcie konieczne okazało się wykonanie 3 przybliżeń dla Q_h,max oraz 4 przybliżeń dla Q_h,min.

5. Zaprojektowanie uzbrojenia sieci wodociągowej.

Przy sporządzaniu schematu wykorzystano schematy z poprzednich ćwiczeń zawierające rozkład przewodów magistralnych, zaznaczone węzły wraz z ich numeracją, średnicami i długościami przewodów oraz warstwicami. Następnie naniesiono zgodnie z opisanymi kryteriami hydranty, odwodnienia, odpowietrzniki oraz zasuwy. Jeżeli średnica przewodu była większa niż 300mm wtedy równolegle do niej naniesiono przewody rozbiorcze o średnicy 100 mm, na których umieszczono wymagane uzbrojenie sieciowe.

Urządzenie regulujące przepływy: zawory, zasuwy

W trakcie rozmieszczania zasuw na schemacie kierowano się następującymi kryteriami:

- Zasuwy liniowe na przewodach magistralnych umieszczono na początku i na końcu odcinka oraz pomiędzy końcami tak, aby odległości między zasuwami nie wychodziły poza przedział 400 ÷ 700 m.

- Zawory węzłowe umieściłem zgodnie z rozmieszczeniem węzłów przewodów magistralnych w sieci.

Urządzenie czerpalne: hydranty, zdroje uliczne

Głównym kryterium, którym kierowano się przy rozmieszczaniu hydrantów był wymóg by nie były one od siebie więcej niż 100m. Jest to ważne ponieważ hydranty pełnią istotne funkcje zarówno w sytuacjach pożarowych jak i w przypadkach innych awarii.

Urządzenia zabezpieczające : wydłużki, odpowietrzniki, zawory regulacyjne, odwodnienia.

Z tej grupy urządzeń na schemacie umieszczono odpowietrzenia oraz odwodnienia. Odpowietrzenia umieszczono za zasuwą w najwyższym odcinku danego przewodu. Natomiast odwodnienia umieszczono w najniższym miejscu danego przewodu.

Uzbrojenie projektowanej sieci wodociągowej zostało dołączone do projektu.

6. Sporządzenie wykresu linii ciśnień.

Do sporządzenia wykresu linii ciśnień wykorzystano wartości obliczeniowe wyznaczone metodą Crossa.

W celu obliczenia ciśnienia wymaganego posłużono się wzorem:

H_w — wysokość ciśnienia wymaganego w węźle,

(2,8 ÷ 3,0) — wysokość kondygnacji,

n — liczba kondygnacji w danej zabudowie,

(0,8 ÷ 1,5) — straty ciśnienia przy przepływie przez przewody poziome,

1 — strata ciśnienia na wodomierzu głównym,

2,5 — strata ciśnienia na wodomierzu mieszkaniowym,

10 — wysokość wymaganego ciśnienia w dowolnym miejscu instalacji.

W celu uzyskania rzędnej linii ciśnienia należało wykonać następujące obliczenie:

Rz_Lc — rzędna linii ciśnienia w węźle,

h_A-B — straty na odcinku A-B,

Rz_t — rzędna terenu,

H — ciśnienie w węźle.

W projekcie przyjęto:

Strefa zagospodarowania przestrzennego	Liczba kondygnacji	straty ciśnienia przy przepływie przez przewody poziome
Zabudowa wysoka	5	0,8
Zabudowa niska	3	1,1
Zabudowa jednorodzinna	1	1,5

7. Obliczenia pompowego ujęcia wody.

Zadanie polegało na zaprojektowaniu pompowego układu ujęcia wody za pomocą studzien wierconych o wydajności odpowiadającej maksymalnemu dobowemu zapotrzebowaniu na wodę z ćwiczenia nr 1 - Q_d,max = 8810 [m³/d] = 0,1020 [m³/s]

Dane hydrogeologiczne potrzebne do wykonania ćwiczenia:

• wysokość ciśnienia piezometrycznego nad spągiem warstwy wodonośnej H = 39 [m]

• miąższość warstwy wodonośnej m = 18 [m]

• współczynnik filtracji k_f= 12 [m/d] = 0,00014 [m/s]

• średnica zewnętrzna filtru d_z = 508 [mm] = 0,508 [m]

• położenie statycznego zwierciadła wody w studni pod powierzchnia terenu 33 [m]

1. Wyznaczenie charakterystyki studni i filtru

Charakterystyka studni to zależność między jej wydatkiem a wysokością depresji s, która mierzona jest od poziomu statycznej linii ciśnień w głąb ziemi.

Aby wyznaczyć charakterystykę studni, skorzystałem ze wzoru na wydatek:

Zasięg leja depresji obliczyłem ze wzoru:

Charakterystyka filtru to zależność pomiędzy wydatkiem filtru a wysokością filtru.

Dopuszczalna prędkość wlotowa została obliczona ze wzoru

Z wykresu charakterystyki studni i filtru odczytano wysokość depresji s, w wyniku przecięcia się charakterystyki studni i wartości wydatku eksploatacyjnego studni Q_eks.

Przy założeniu, że:

2. Ustalenie niezbędnej liczby studzien:

Dzięki wartościom odczytanym z wykresu charakterystyki studni i filtru, możliwe jest obliczenie niezbędnej liczby studzien do zaspokojenia całkowitego dobowego zapotrzebowania na wodę dla miasta.

Liczbę studzien wyznaczono ze wzoru:

Wydajność studni wyznaczono ze wzoru:

Promień leja depresji:

Liczba studzien:

Wydajność studni:

Dla
odczytano:

Studnie rozmieszczone są blisko siebie więc należy uwzględnić ich współdziałanie zatem dla warunku
oraz dla L/R=0,76 przyjmujemy współczynnik b = 0,86.

Uwzględniając go skorygowana liczba studni zmienia się na n = 11.

Zatem
i odczytane dla niego s = 3,51 [m] i R = 124 [m]

Biorąc pod uwagę, że promień leja depresji jest większy niż odległość między studniami musimy wziąć zastępczy promień leja depresji.

Liczy się go dodając do odległości skrajnych studzien podzielona przez 4 i odczytany promień.

Czyli w naszym przypadku będzie to 200/4 + 124 co daje zastępczy promień równy 174 [m].

Obliczenie wydatku studzien przy uwzględnieniu ich współdziałania:

Obliczenie to wykonuje się w przypadku, gdy odległość pomiędzy studniami jest mniejsza niż promień leja depresji, wytworzonego wskutek użytkowania studni.

t_X - obniżenie zwierciadła wody w studni,

L - odległość pomiędzy dwiema oddziałującymi studniami.

β_X - współczynnik wpływu dla kolejnej studni.

Obliczenia:

dla 1 studni na którą działa tylko studnia nr 2

dla studni 2 na którą działa studnia 1 i 3

Zaprojektowany zespół studzien działa w ten sposób, że studnia 6,7 i 11 działają na identycznej zasadzie jak studnia 1. Natomiast studnia 3,4,5,8,9 i 10 na takiej jak studnia 2.

W celu wyznaczenia sumarycznego wydatku zespołu studzien stosujemy wzór:

Wydatek zaprojektowanego zespołu studzien jest wyższy od Q_d,max, ale mieści się w granicy błędu 2%. Dlatego obliczenia uważam za poprawne.

Obliczenia hydrauliczne przewodów tłocznych:

Wymagane ciśnienie na stacji uzdatniania wody (STU) wynosi 7 m nad powierzchnią terenu, pompy w studniach muszą wytworzyć takie ciśnienie by pokryć te wymagania. Zatem, aby obliczyć linię ciśnień na wlocie do stacji uzdatniania, skorzystano ze wzoru:

Gdzie Rzt- rzędna terenu która w moim projekcie wynosi 119m zatem,

Rzędną linii ciśnienia w pozostałych w pozostałych węzłach przewodu tłocznego obliczone zostały wg wzoru:

∑h_i-st - suma strat ciśnienia na drodze od stacji uzdatniania do punktu i

Suma strat, jak i średnica i straty odcinkowe odczytano z nomogramu do wymiarowania sieci wodociągowej.

Aby obliczyć wymaganą wysokość podnoszenia pompy w studni, skorzystano ze wzoru:

Przykładowe obliczenia dla wysokości podnoszenia:

• studni pierwszej:

dla

• studni siódmej:

dla

Dobór pompy:

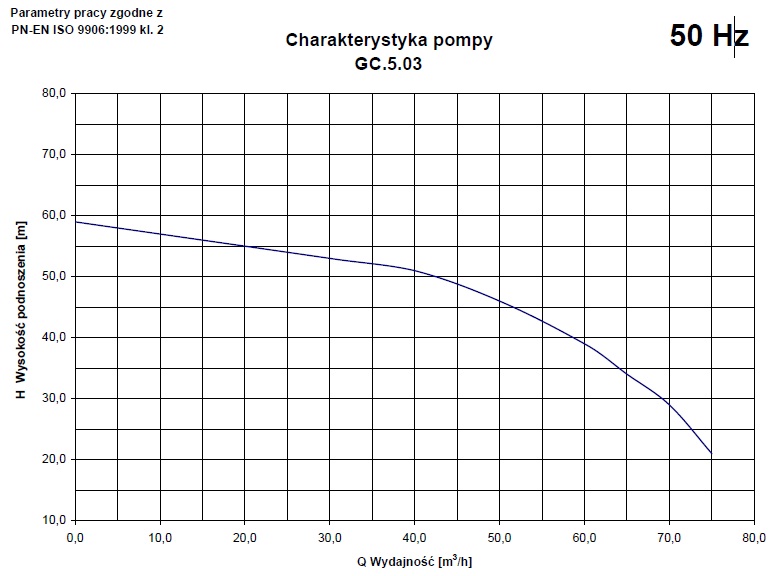
Dla tych wartości dobrałem pompę głębinową GC.5.03 firmy HYDRO-VACUUM.

Jest ona dobrana nieco nad wyrost w stosunku do zapotrzebowań jednak pompa tego samego typu o niższych parametrach nie zapewniałaby już odpowiedniej wysokości podnoszenia.

Dla potrzebnego strumienia Q odczytano z wykresu wysokość pompowania. Jest ona wyższa niż potrzebna, należy więc zastosować dławienie.

Wartości wysokości dławienia H_d obliczyłem na podstawie wzoru:

Gdzie:

H_p - wysokość podnoszenia odczytana z wykresu charakterystyki ,m

H_pw - wymagana wysokość podnoszenia pompy, m

Wartości wysokości dławienia dla pomp wyniosły odpowiednio:

Wszystkie obliczenia zostały przedstawione w tabeli poniżej:

Nr węzła	Nr odcinka	Przepływ na odcinku [l/s]	Długość odcinka L [m]	Średnica D [mm]	Prędkość przepływu v [m/s]	Jednostkowy spadek ciśnienia i [‰]	Straty ciśnienia na odcinku h [m]	Rzędna linii ciśnień [m n.p.m.]	Rzędna wysokości podnoszenia pompy [m n.p.m.]	Wymagana wysokość dławienia Hd [m]
St 1								132,08	134,99	2,91
		St 1 - A	9	48	100	1,15	26,5				0,27
	A																		131,81
												A - B	9	100	100	1,15	26,5	2,65
	B																		129,16
												B - C	18	100	150	1,02	12,6	1,26
	C																		127,90
												C - D	27	150	200	0,86	6,3	0,95
	D																		126,95
												D - E	54	250	300	0,76	2,9	0,73
	E																		126,22
												E - STU	99	100	400	0,79	2,2	0,22
	STU																		126,00
	St 7																		131,35	134,99	3,64
												St 7 - G	9	48	100	1,15	26,5	0,27
	G																		131,08
												G - H	9	100	100	1,15	26,5	2,65
	H																		128,43
												H - I	18	100	150	1,02	12,6	1,26
	I																		127,17
												I - J	27	150	200	0,86	6,3	0,95
	J																		126,22
												J - STU	99	100	400	0,79	2,2	0,22
	STU																		126,00

28

Współczynniki cząstkowe:

Współczynnik cząstkowy	l/sha
qZW	2,34
qZN	0,46
qZJ	2,86
qP	0,33
qU	0,39

k_f - współczynnik filtracji gruntu,

m - miąższość,

s - depresja,

R - zasięg leja depresji,

r - promień studni.

Q_f - eksploatacyjna wydajność studni,

d_f - średnica zewnętrzna filtru,

l_f - długość filtru,

v - średnia prędkość wlotowa do filtru.

---