Ćwiczenia 02 - Rachunek wektorowy

Zadanie 1

Wyznaczyć moment siły F = i + 3j + 2k zaczepionej w punkcie A(2, -2, -3) względem punktu B(0, 2, -5). Określić również ramię tej siły względem punktu B. Współrzędne siły wyrażone są w [N], natomiast punktów w [m].

Rozwiązanie

Na podstawie definicji:

„Momentem M⁰ siły F względem punktu 0 (bieguna) nazywamy iloczyn wektorowy wektora promienia r łączącego biegun z początkiem siły F przez wektor tej siły

.

Innymi słowy, jest to wektor M^O, prostopadły do płaszczyzny utworzonej przez wektor siły F oraz wektor promień r przechodzący przez punkt O. Zwrot wektora momentu wynika z właściwości iloczynu wektorowego.

Po wyrażeniu wektorów r, F i M^O w ortokartezjańskim układzie współrzędnych

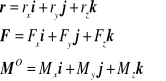
otrzymujemy

”

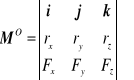
(1)

Z rysunku wynika, że

czyli

Po wstawieniu do wzoru (1) wektora promienia r i danej siły F mamy

Korzystając z postaci wyznacznikowej iloczynu wektorowego otrzymujemy

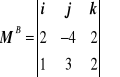
i po obliczeniu

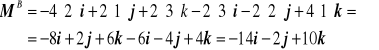
Moduł wektora momentu M^B wynosi więc

a jego kosinusy kierunkowe wynoszą odpowiednio

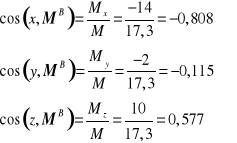
Wykorzystując właściwości momentu siły względem punktu, możemy wyznaczyć ramię h siły F względem punktu B, a mianowicie

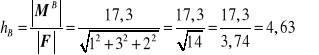
[m]