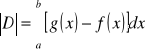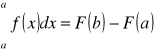
CAŁKI OZNACZONE:

WZÓR NEWTONA-LEIBNIZA:

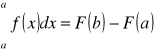
CAŁKOWANIE PRZEZ

CZĘŚCI: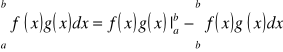

PODSTAWIANIE: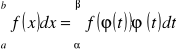

WŁASNOŚCI CAŁEK:

1. Jeśli f jest całkowalna na przedziale [a, b], a funkcja g różni się od funkcji f jedynie w skończonej liczbie punktów z przedziału [a, b], to g też jest całkowalna i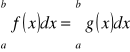
   .

2. Jeśli f jest całkowalna na [a, b], to:

1. Dla dowolnego
   

2. 
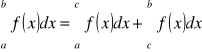
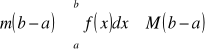
   , gdzie m i M są dowolnymi liczbami, takimi że
   dla
   .

3. Jeżeli funkcje f i g są całkowalne na [a, b], to:

1. 
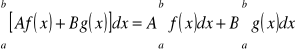
   , dla dowolnych liczb
   .

2. 
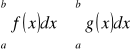
   , gdy
   , dla
   

4. Pole figury: