LOGIKA I METODOLOGIA NAUK #6

Elementy teorii relacji

Relacje są zawsze zbiorami, obiektami abstrakcyjnymi.

x kocha y-a

Ważna jest kolejność!

Relacja to zbiór par (możemy mówić o konkretnej parze).

Relacje - zbiory dystrybutywne, w środku są pary uporządkowane a obiekty są abstraktami

• Pojęcia umożliwiające zdefiniowanie relacji:

- para (n-tka) uporządkowana x ≠ y <x,y> ≠ <y,x>

- iloczyn kartezjański

Symbol - …x…

X x Y = {<x,y>: x
X
y
Y}

Przykłady:

{a,b,c} x {b,d} = {<a,b>, <a,d>, <b,b>, <b,d> <c,b>, <c,d>}

L={ x: x jest człowiekiem} Mamy: LxL = {<x,y>: x,y
L}

*Pojęcie pary uporządkowanej można rozszerzyć na pojęcie n-tki uporządkowanej.

<x₁, x₂, …, x_n>

a b para
do iloczynu kartezjańskiego

Relacja: x bezpośrednio poprzedza y w alfabecie języka polskiego.

Rozważana relacja poprzedzania jest następującym zbiorem: {<a,b>, <c,d>}

Każda relacja jest podzbiorem określonego iloczynu kartezjańskiego.

Definicja

R jest relacją 2-argumentową w zbiorze x wtedy, gdy ∃y₁, ∃y₂ (Y₁, Y₂ x oraz R Y₁ x Y₂)

{ } x { } = { < , >}

{ , } { < , >}

Ø {< , >}

Dziedzina (lewa dziedzina) relacji R:

D_l (R) = {x: ∃y x Ry}

Przeciwdziedzina (prawa dziedzina) relacji R:

D_p (R) = {y: ∃x x Ry}

Pole relacji

P (R) = D_l (R)
D_p (R)

Przykłady:

{a,c,e}, {b,d}

R = {<a,b>, <c,d>} Mamy:

1. D_l (R) = {a,c}

2. D_p (R) = {b,d}

3. P (R) = {a,c}
   {b,d} = {a,b,c,d}

Zbiory: M = mężczyźni, L = ludzie, relacja: x jest synem y-a:

S = {<y>
M x L: x jest synem y-a} Mamy:

1. D_l (S) = M

2. D_p (S) =ludzie mający syna

3. P (S) = M
   ludzie mający syna

Relacje można odwracać (konwers relacji)

R ^-1 (zbiór par, tylko odwrotnych)

R ^-1 = {<y,x>: x Ry}

Przykłady:

1. R = {<a,b>, <c,d>}
   R ^-1 = {<b,a>, <d,c>}

2. S = { <x,y>
   M x L: x jest synem y-a}
   S ^-1 = {<x>
   L x M: y jest matką lub ojcem mężczyzny}

3. W = relacja bycia zwierzchnikiem
   W ^-1 = relacja bycia podwładnym

W = {a,b,c}

• W x W = {<a,a>, <a,b>, <a,c>, <b,a>, <b,c>, <c,a>, <c,b>, <c,c>}

• 
  X jest starszy od y-a

S(W) = {<x,y>: x jest starszy od y-a} = {<b,a>, <c,b>, <c,a>}

• 
  
  D_l (S) = {b,c}

• 
  D_p (S) = {a,b}

• P (S) {b,c}
  {a,b} = {a,b,c}

• Id (W) = {<a,a>, <b,b>, <c,c>}

• D_l (Id) = {a,b,c} = D_p (Id) = P (Id)

• S
  Id = {<b,a>, <c,b>, <c,a>, <a,a>, <b,b>, <c,c>}

• relacja macierzyństwa w zbiorze ludzi

relacja ojcostwa w zbiorze ludzi

• x jest uczniem y-a

x jest nauczycielem y -a

• S
  Id = Ø

• D_l (S) = Ø

• D_p (S) = Ø

• P (S) = Ø

• S - Id = S

• -S = {<a,a>, <a,b>, <b,b>, <b,c>, <c,c>}

konwers relacji S

S^-1 (W) = {<a,b>, <b,c>, <a,c>}

Konwers i dopełnienie to coś różnego!

Relacje można „składać” - otrzymujemy iloczyny względne - symboliczne R ; S

R ; S = {<x,y>: ∃z (x Rz
zSy)}

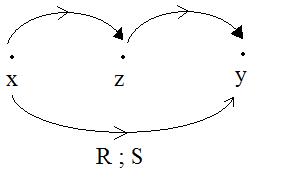
Np.:

• R = relacja bycia ojcem

R ; R = relacja bycia dziadkiem ze strony ojca

• R = relacja bycia terapeutą

S = relacja bycia ofiarą (przemocy)

R ; S = relacja bycia terapeutą ofiary (przemocy)

L

Ar P

<K,J>

<M,J>

<J,M>

<K,M>

<Ar,P>

a

b

c

e

d

a

b

c

d

e

L

K

M

P

J

M

A

a

b

c

a

b

c

a

b

c