ZBIÓR ZADAŃ PRZYGOTOWAWCZYCH DO MATURY Z MATEMATYKI
I. Działania na liczbach
Zaznacz na osi liczbowej zbiory A i B, a następnie wyznacz zbiory A∪B, A∩B, B\A, jeśli
A = <- 3,1), B(0,5〉.Dane są zbiory A = {x∈R: x > - 2 ∧ x ≤ 5} B = {x∈R: x ≤ 0}. Wyznacz zbiory A∪B, A∩B, B\A, A\B.
Zapisz symbolicznie za pomocą przedziałów zbiory: A - zbiór liczb rzeczywistych mniejszych od 2, B - zbiór liczb rzeczywistych większych od - 5 a następnie wyznacz zbiory A∪B, A∩B, B\A.
W układzie współrzędnych naszkicuj wzór A\B jeśli A = {(x, y): x∈R ∧ y∈R ∧ x2 + y - 4x ≤0};
B = { (x, y): x∈R ∧ y∈R ∧ x - y≥0 }.Niech A = {x∈R: x2 - 2x - 3≤0} oraz B = { x∈R: 4 - x2>0}. Wyznacz zbiory A, B, A∩B.
Zaznacz na osi liczbowej zbiór A'∩ B, jeśli A = ( - ∞, - 4) ∪ (4,6) ∪ (6, + ∞), B = (l, 5).
Zaznacz na osi liczbowej zbiory A = {x∈R: |x| >4}, B = {x∈R: |x + l|≤3} oraz zbiory: A∪B, A∩B, A\B.
Niech A = {(x, y): x∈R ∧ y∈R ∧ y ≥ |x + 5| } i B = {(x, y): x∈R ∧ y∈R ∧ y - 3 x< 5 }. Na płaszczyźnie zaznacz zbiór punktów należących do zbioru A∩B.
Liczby całkowite a, b, c przy dzieleniu przez 7 dają reszty odpowiednio 1, 2, 3. Oblicz resztę z dzielenia liczby a2 + b2 + c2 przez 7. (Odp: 0)
Oblicz. a)
; b)
; c)
Oblicz:
liczby a wiedząc, że
13. Usuń niewymierność z mianownika i wykonaj działania: a)
; b)
;
c)
, d)
.
14. Oblicz:
.
15. Dane są liczby p = l +
, q = 2 -
, r = - 3 +
. Zapisz liczbę
w postaci a + b
·
16. Uzasadnij, że
jest równa
+ l.
Oblicz wartość wyrażenia
dla x =
, y =
.Wykaż, że liczba ((l +
)3 + (1 -
)3)
jest liczbą wymierną.Wiedząc, że a, b
C + i a > b porównaj ułamki
.
Dane wyrażenie (3a - l)(3a + l) - 8a2 zapisz w najprostszej postaci, a następnie oblicz jego wartość dla
. Poda wynik z dokładnością do 0,01.Podane iloczyny 4000·200 i 0,0007·0,3 można zapisać w następujący sposób:
4000·200 = 4·103·2·102 = 8·105
0.0007·0,3 = 7·10 - 4·3·10 - 1 = 21·10 - 5
Zapisz podobnie: 80000·6000 oraz 0,013·0,00007.
22. W dziesiątkowym systemie pozycyjnym zapis 100101 oznacza liczbę
l·105 + 0·104 + 0·103 + l·102 + 0·101 + l·10 a w systemie dwójkowym ten sam zapis oznacza liczbę l·25 + 0·24 + 0·23 + l·22 + 0·21 + 1·2 = 37. W systemie dwójkowym zapisano liczby 111 i 1011111. Zapisz te liczby w systemie dziesiątkowym
Rozłóż na czynniki pierwsze liczbę 24180.
Wyznacz największy wspólny dzielnik liczb 32670 i 12375.
Wiemy, że a∈<2, 3〉, b∈<4, 5〉. Jakie wartości może przyjmować wyrażenie a + b, a jakie a : b.
Podaj największą liczbę pięciocyfrową o różnych cyfrach podzielną przez 9.
Nie korzystając z kalkulatora porównaj liczby 230 + 230 i 415.
30. Sumę kolejnych liczb nieparzystych od 1 do 999 czyli S = 1 + 3 + ... + 995 + 997 + 999 można obliczyć grupując składniki parami: S = (1 + 999) + (3 + 997) + .. . + (499 + 501) tak, że suma liczb każdej pary wynosi 1000. Par jest 250, bo składników było 500 stąd S = 250·1000 = 250000. Analogicznie oblicz sumę S = 5 + 10 + .. . + 990 + 995 + 1000.
31. Uzasadnij, że a)
; b)
.
32. Uzasadnij, że kwadrat liczby nieparzystej przy dzieleniu przez 8 daje resztę 1.
Nie korzystając z kalkulatora uzasadnij, że 274 = 9·38·32
34.Dane są liczby x = 2 - 5
i y = l -
. Oblicz x + y, x - y, x · y, x/y, a otrzymane wyniki zapisz w postaci a + b
.
II Procenty
Po podwójnej obniżce ceny, najpierw o 20%, a później o 5%, spodnie kosztują 114zł. Jaka była cena spodni przed obniżkami?
Stopiono 2 kg stopu o zawartości 24% i 5kg stopu o zawartości 35%. Ile procent miedzi zawiera otrzymany stop?
Z naczynia zawierającego 10 litrów 3% wodnego roztworu soli odlano połowę, a następnie dodano 7 litrów czystej wody. Jakie jest stężenie soli w nowym roztworze?
Komputer kupowany za gotówkę kosztuje 2000zł, a kupiony na raty jest o 20% droższy. Przy kupnie na raty trzeba wpłacić 400zł, a resztę w pięciu równych ratach. Jaka jest wysokość jednej raty?
Ile otrzymasz pieniędzy po 3 latach z tytułu lokaty w wysokości 2000zł oprocentowanej 21 % w stosunku rocznym, jeżeli odsetki są dopisywane na koniec rocznego okresu oszczędzania?
Ile procent wszystkich liter w wyrazie Małgorzata stanowią litery a?
Napój pomarańczowy A zawiera 15% soku pomarańczowego. Ile litrów każdego napoju należy wymieszać, aby otrzymać 10 litrów napoju zawierającego 10% soku pomarańczowego?
Pewien zakład pracy zatrudniał 20 pracowników. Ich średnie miesięczne wynagrodzenie wynosiło 600zł. Gdy zatrudniono jeszcze jednego pracownika, to średnia płaca miesięczna wszystkich pracowników wzrosła o 0,5%. Oblicz, jakie wynagrodzenie otrzymał nowo zatrudniony pracownik.
Długopis kosztuje tyle samo co notes. Jeśli długopis podrożeje o 6%, a notes o 4%, to o ile procent więcej trzeba zapłacić za 3 takie długopisy i 3 notesy?
10. Jakim procentem liczby k =
jest liczba l =
?
Rodzice Ewy kupili kuchenkę mikrofalową za 999zł. Tata powiedział, że podatek od tego zakupu wynosi 22% Ewa chciała znać cenę netto i szybko policzyła za pomocą kalkulatora, że będzie to 779,22zł, ale tata się z tym nie zgodził. Jaka jest cena netto kuchenki?
Ojciec Marka chce złożyć w banku 5000zł na okres jednego roku. Ma do wyboru dwa banki. W jednym oprocentowanie półroczne wynosi 8%, a w drugim oprocentowanie roczne 17,5%. Wybór którego banku byś mu doradził, jeśli w pierwszym banku odsetki dopisuje się co pól roku, a w drugim co rok?
Przedsiębiorca mając 720000zł kupił dom. Trzecią część pozostałych pieniędzy umieścił w banku na 8%, a resztę na 10%. Pieniądze oddane na procent przyniosły po roku 2352zł odsetek. Ile zapłacił za dom?
Liczba ludności pewnego miasta wynosi obecnie około 1 %. Czy liczba ludności w tym mieście za pięć lat przekroczy 1050000?
Stężenie pewnego kwasu wynosi 30%. Ile wody należy dolać do 2 litrów tego kwasu, aby stężenie zmniejszyło się do 25%?
Zwiększając o 3 pewną liczbę naturalną n, która jest większa od 50, zwiększamy ją o więcej niż 5,5%. Jaka to liczba?
Jola i Bartek wyruszyli jednocześnie z tego samego domu do szkoły .Długość kroku Joli jest o 10% mniejsza od długości kroku Bartka , ale Jola robi w tym samym czasie o 20% kroków więcej niż Bartek. Kto pierwszy dotrze do szkoły ?
Dwie trzecie pewnego towaru sprzedawca sprzedał z zyskiem 20% , 25% towaru z zyskiem 40% a pozostała część z zyskiem 30% . Jaki procentowy zysk uzyskał ze sprzedaży tego towaru ? Wynik podaj z dokładnością do części dziesiątych.
68% liczby x wynosi
. Znajdź tę liczbę.
III Zadania tekstowe
W pewnym sklepie wszystkie pomarańcze mają jednakową wagę 180 gramów. Klient prosząc o k kg pomarańczy dostaje najmniejszą liczbę pomarańczy n, których łączna masa nie przekracza już k. Ile sztuk pomarańczy dostaje klient, jeśli zechce kupić l,5kg pomarańczy?
Ile kosztuje ogrzewanie pomieszczenia grzejnikiem o mocy 2000W przez 8 godzin, jeśli 1kWh energii kosztuje 30 groszy (1kW = 1000W)?
Na spektaklu teatralnym wszystkie miejsca były zajęte. W każdym rzędzie siedziała jedna dziewczynka, a resztę miejsc zajmowali chłopcy. Rzędów było tyle, ile miejsc w jednym rzędzie. Wiadomo, że na sali siedziało więcej niż 200 osób, a mniej niż 230. Ilu było chłopców i ile dziewcząt w teatrze?
Rozwiąż zadanie z XVIII wieku: „Złodziej uciekający ubiega na dzień mil 5. Pogoń w 8 dni po ucieczce za nim wysłana ujeżdża na dzień mil 7. Za ile dni dogoni złodzieja i jak wiele mil ucieknie złodziej, nim będzie dogoniony?"
Udowodnij, że iloczyn dwóch liczb postaci 4n + l, n
N jest liczbą tej samej postaci.
6. Sprzedawca sprzedaje za 2zł: 5 gruszek lub 8 jabłek. Zosia kupiła 20 sztuk tych owoców i zapłaciła 5,60zł. Ile kupiła jabłek, a ile gruszek?
7. Marek szedł z domu do punktu odległego o 1km z prędkością 2 km/h, a wracał z prędkością 6 km/h. Z jaką średnią prędkością Marek pokonał trasę w obie strony?
8. Odpowiadając na każde z 20 pytań tekstu wyboru można zyskać 5 punktów za dobrą odpowiedź albo stracić 1 punkt za brak odpowiedzi lub złą odpowiedź. Na ile pytań musisz odpowiedzieć dobrze, aby uzyskać co najmniej 70 punktów?
9. Na podstawie wzoru F = m · a, wynikającego z II zasady dynamiki Newtona, wyznacz masę ciała m z dokładnością do 0,05kg wiedząc, że F = 3,l·104kg·m/s2, a = 9,8m/s2.
10. Banknot 10 zł rozmieniono na 11 monet o wartości 50 groszy i 2 zł. Ile było monet każdego rodzaju?
11. Po zważeniu wszystkich uczniów klasy la otrzymano następujące wyniki w kg:
58 48 55 46 75 44 73 78 52 70 67 72 55 80 54 70 66 62 54 58 53 60 68 45 66 58 59 51 64 68.
Policz, ile wyników zawartych jest w każdym z przedziałów: 41 ÷ 50, 51 ÷ 60, 61 ÷ 70, 71 ÷ 80 i zilustruj tę zależność na diagramie słupkowym.
13. Suma cyfr liczby dwucyfrowej jest równa 12. Jeżeli do tej liczby dodamy 36 to otrzymamy również liczbę dwucyfrową zapisaną tymi samymi cyframi, ale w odwrotnym porządku. Jaka to liczba?
14.Piechur w ciągu trzech dni przeszedł 44 km. Drugiego dnia przeszedł o 8 km mniej niż pierwszego dnia, a trzeciego dwa razy tyle co drugiego dnia. Ile kilometrów przeszedł piechur każdego dnia?
Bilet autobusowy normalny z Łodzi do Krynicy Górskiej (odległość 400 km) kosztuje 44zł. Oblicz ile osób musiałoby pokonać tę samą trasę samochodem osobowym, aby koszt spalonej na trasie benzyny był mniejszy niż łączna cena biletów autobusowych dla tej grupy osób. Przyjmij, że samochód spala średnio 81 benzyny na l00km, a cena 11 wynosi 3,50zł i kierowca może zabrać maksymalnie 5 osób.
Głos w powietrzu rozchodzi się z prędkością 330 m/s, a w wodzie w ciągu 0,2s dociera na odległość 287m.
a. W którym z tych dwóch środowisk głos ma większą prędkość i ile razy?
b. W jakim czasie głos pokona 1,5 km w wodzie, a w jakim w powietrzu?
Na mapie w skali 1:100000 dwie miejscowości oddalone są od siebie o 32,4 cm. Jaka jest rzeczywista odległość między tymi miejscowościami w kilometrach?
Trzej przyjaciele kupili wspólnie 360 akcji firmy LUX wnosząc - odpowiednio 15000zł, 20000zł, 25000zł Rozdziel akcje między trzech przyjaciół odpowiednio do wniesionych wkładów pieniężnych,
19. Każda z bakterii pewnego rodzaju dzieli się na dwie co pół godziny. Ile bakterii może powstać z jednej w ciągu pięciu godzin?
Samolot przebywa pewna drogę w 36 minut - . W jakim czasie przebędzie tę samą drogę, jeżeli będzie leciał z prędkością o 25% mniejszą?
Surowiec |
Cena 1 tony w dolarach |
Aluminium |
1410 |
Cynk |
1160 |
Nikiel |
7805 |
Miedź |
1880 |
Ołów |
470 |
Kilku uczniów prenumeruje pewne czasopismo, za które roczna opłata wynosi 480zł. Gdyby przyłączyło się dalszych czterech uczniów do spółki, to koszt na każdego ucznia zmniejszyłby się o 20zł rocznie. Ilu uczniów prenumeruje czasopismo?
22. Oto tabela cen surowców. Ile można kupić ton ołowiu za l0000 ton miedzi?
23. Żeglarz wybierający się w samotny rejs dookoła świata, zabrał pewien zapas żywności. Jeśli będzie zjadał codziennie po l,25kg to zapas wyczerpie się po dwóch miesiącach. Jaka powinna być masa dziennej porcji jedzenia, aby zapas wystarczył żeglarzowi, na 2,5 miesiąca?
24. Koszt wynajęcia autobusu na wycieczkę wynosi 150zł. Gdyby 5 uczniów pewnej klasy zrezygnowało z wycieczki, to każdy z pozostałych płaciłby o 1 zł więcej. Ilu uczniów liczy klasa?
IV Ogólne własności funkcji
Wyznacz dziedzinę funkcji f(x) =
, gdzie g(x) =
h(x) =
.Wyznacz zbiór wartości funkcji: f(x) =
, g(x) = |3x - 2| - 5.Niech f(x) =
. Podaj dziedzinę, miejsca zerowe oraz współrzędne punktu przecięcia wykresu tej funkcji z osią OY.Wyznacz dziedzinę i miejsca zerowe funkcji danej wzorem f(x) =
.Wyznacz miejsca zerowe funkcji f(x) =
.Oblicz miejsca zerowe funkcji: f(z) =
g(x) = 3x(x - 5)(x2 + 9).Czy funkcje f(x) i g(x) są równe jeśli: f(x) =
i g(x) = x + 2 oraz f(x) =
i g(x) = x + 3.Czy funkcje określone wzorami f(x) = x2 - 4 i g(x) = 0,5x2 - 2 są równe? Odpowiedź uzasadnij.
Podaj funkcję wyjściową i zapisz jakie kolejne przekształcenia należy wykonać aby otrzymać wykres funkcji: f(x) = |x2 - |x| + 4|; g(x) = 1 - 2|x - 4|; h(x) = ||x - 3| - 2| - 1; k(x) =
.Oblicz: |3 - 2
|,
,
,
.Doprowadź do najprostszej postaci:
dla x< - 1
dla x< - 4
dla x
( - 4, - 1)
V Funkcja liniowa
1. Rowerzysta porusza się ze stałą prędkością 20km/h. Podaj wzór, który opisuje zależność przebytej drogi y (w kilometrach) od czasu jazdy x (w godzinach).
2. Dana jest częściową tabelka funkcji liniowej, której dziedziną jest zbiór liczb rzeczywistych. Znajdź wzór tej funkcji:
x |
- 2 |
- 1 |
2 |
y |
- 1 |
0 |
3 |
4. Ułóż zadanie tekstowe do podanego równania i rozwiąż je
5. Napisz wzór funkcji liniowej, której wykres jest prostopadły do wykresu funkcji y =
i przechodzi przez punkt o współrzędnych ( - 1, 11).
6. Uzasadnij, że dla każdej funkcji liniowej f oraz dla każdego n
N prawdziwa jest równość
f(n - l) + f(n + l ) = 2f(n).
7. Dla jakich wartości argumentów x jednocześnie: wartości funkcji f(x) =
+ 2 są dodatnie, a wartości funkcji g(x) = 2x - l są ujemne?
8. Wyznacz wzór funkcji liniowej wiedząc, że f(5) - f(4) = 3 oraz f(3) = 2.
9. Podaj definicję funkcji liniowej. Napisz wzór funkcji liniowej, jeśli f(4) = 3 i f(x)>0
10. Narysuj wykres funkcji y = f(x) x∈<- 2, 5〉, y∈<- l, 3〉 i posiadającej następujące własności:
a. odwzorowuje <- 2, 5〉 na <- l, 3〉
b. f( - 2) = l, f(- l) = 0, f(0) = - l
c. dla x
(0,3〉 funkcja jest rosnąca i f(3) = 3
d. dla x
(3,5〉 funkcja jest malejąca i f(5) = 1 Czy istnieje jedna taka funkcja?
11. Dla jakich wartości parametru k jednocześnie funkcja f(x) = (2k - 1)x + 3 jest malejąca, a funkcja
g(x) = kx + (l - 3k) jest rosnąca?
12. Wyznacz wzór funkcji liniowej, której miejsce zerowe jak i współczynnik kierunkowy wynosi
.
13. Dla funkcji f(x) = ax + b wyznacz takie liczby a i b, żeby f(2) = 4 i f(m - l) = f( - 2 + m).
14. Wyznacz takie wartości m, dla których funkcja liniowa f(x) = (lm - 2l - 3)x + 2m jest malejąca i nieparzysta.
Środek transportu |
I |
II |
Wzór funkcji |
y = 50x + 150 |
y = 25x + 250 |
15. Zależność kosztu przewozu y od długości pracy x (w kilometrach ) dwoma różnymi środkami transportu określają funkcje:
Przy jakich odległościach x bardziej ekonomiczny jest II środek transportu?
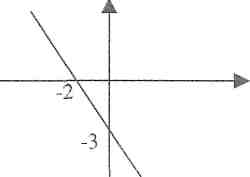
17. Podaj wzór funkcji, której wykres przedstawiono na rysunku
18. Rozwiąż równanie:
Rozwiąż równanie x + y
dla x, y
w zależności od parametru k.
25. Zapisz wyrażenie
w najprostszej postaci, jeśli wiadomo, że x
<- 3, 0〉.
26. Narysuj wykres funkcji określonej wzorem
27. Rozwiąż równania i nierówności:
|3x - 5| = - 5
28. Podaj miejsce zerowe funkcji f(x) = 1 - |2x - 3|.
29. Narysuj wykres funkcji określonej wzorem f(x) =
i podaj zbiór wartości tej funkcji i przedziały, w których funkcja przyjmuje wartości ujemne.
30. Wykonaj wykresy funkcji:
f(x) = 2x - |4x - 8|
f(x) = |x - 1| + |x + 3|
f(x) = -
f(x) = ||1 - x| - 3|
31. Narysuj wykres funkcji f(x) = |x| - 2 i odczytaj z wykresu zbiór rozwiązań nierówności f(x)>0.
32. Sporządź wykres funkcji danej wzorem f(x) =
36. W układzie współrzędnych zaznacz zbiór punktów, których współrzędne spełniają układ warunków
.
37. Oblicz pole trójkąta określonego układem nierówności
38. Przedstaw interpretację graficzną układu nierówności
39. Oblicz pole figury ograniczonej wykresem funkcji f(x) =
40. Dla jakich wartości parametru m rozwiązaniem układu
jest para liczb dodatnich?
41. Dla jakich wartości parametru m rozwiązanie układu równań
jest para liczb ujemnych?
42. Wyznacz parametry m i n, tak aby układ równań
był nieoznaczony.
43. Dla jakich wartości parametru k układ
jest sprzeczny?
44. Wyznacz parametry m i n, tak, aby rozwiązanie układu równań
była para liczb x = 1, y = 4.
45. Dla jakiej wartości parametru k prosta y = x + k przecina prostą y = 2x − 3 w pierwszej ćwiartce układu współrzędnych?
46. W układzie współrzędnych zaznacz zbiór punktów, których pierwsza współrzędna jest większa od 1, a suma współrzędnych jest nie większa od 4.
47. Rozwiąż układy równań i nierówności:
VI Funkcja kwadratowa
1. Napisz wzór funkcji kwadratowej wiedząc, że do jej wykresu należy punkt A = (2, l) i dla x = l funkcja osiąga najmniejszą wartość y = −l.
2. Znajdź współczynniki a, b, c trójmianu kwadratowego y = ax2 + bx + c wiedząc, że jego wykres przechodzi przez punkty A = (2, - 2), B = (5, 1), C = (0, 6).
3. Wiedząc, że x1 = - 1 i x2 = 3 są pierwiastkami trójmianu kwadratowego ax2 + bx + c o współczynniku a = 2, zapisz ten trójmian w postaci kanonicznej.
Rozłóż na czynniki trójmian kwadratowy x2 - ax - 6a2
Pierwiastki trójmianu kwadratowego y = 2x2 + bx + 6 są liczbami całkowitymi. Oblicz b.
Dla jakich wartości parametru k zbiorem wartości funkcji f określonej wzorem
f(x) = (k - 4)x2 - (2 - k)x + l + 0,5k jest przedział <
, +∞)?Wiedząc, że miejsca zerowe funkcji y = x2 + px + q są równe 2 i - 3, wyznacz parametry p i q.
8. Dla jakich wartości parametru k równanie x2 + kx + 9 = 0 ma dwa różne pierwiastki rzeczywiste?
9. Uzasadnij, że trójmian y = - 2x2 + 4x - 6 nie przyjmuje wartości dodatnich. Jaką największą wartość przyjmuje ten trójmian?
10. O jaki wektor należy przesunąć wykres funkcji y = 3x2, aby uzyskać wykres funkcji y = 3x2 + 6x + 10.
11. Dla n∈{1, 2, ... ,40} liczba obliczona według wzoru f(n) = n2 - n + 41 jest liczbą pierwszą.
a. Oblicz największą i najmniejsza liczbę pierwszą, którą można wyznaczyć za pomocą tego wzoru
b. Czy można wyznaczyć tym wzorem liczbę 547?
Rozwiąż nierówność i zaznacz zbiór rozwiązań na osi liczbowej (x + 4)2 < x2 + 4.
Wyznacz wszystkie liczby całkowite dodatnie spełniające nierówność 2 - (x + 3)2> l - (x - 5)2
Rozwiąż nierówność
Równanie (x - a)2 + (y + 2a)2 = a + 4 ma dokładnie jedno rozwiązanie. Znajdź to rozwiązanie.
Rozwiąż układ nierówności
Rozwiąż układ równań:
18. Narysuj w układzie współrzędnych wykresy funkcji f(x) = - x2 + 6x - 5 oraz g(x) = 3x - 3 i zilustruj rozwiązanie nierówności 3f(x) < g(x).
20. Wyznacz te wartości parametru m, dla których równanie (m - l)x2 - 3x - 2 = 0 ma jeden pierwiastek.
21. Rozwiąż algebraicznie układ równań
22. Rozwiąż graficznie nierówność x2 + 1<
.
25. Wśród wszystkich prostokątów o obwodzie 24cm znajdź ten, którego pole jest największe.
26. Kwadrat ma pole 1. Do długości boku tego kwadratu dodajemy liczbę x (x > - l). Oznacz zmianę pola kwadratu przez f(x) i narysuj wykres funkcji y = f(x). Jak zmieni się pole dla x = - 0,3 a jak dla x = 2?
27. W przedsiębiorstwie koszty produkcji wyrażają się wzorem K(x) =
x3 - 3x2 + 12x dochód ze sprzedanej produkcji wzorem D(x) = 12x - x2, a zysk Z(x) jest różnicą dochodu i. kosztów, x oznacza liczbę jednostek produkcji (x>0).
Przy ilu jednostkach x produkcja jest deficytowa (tzn. zysk jest ujemny)
Dla iłu jednostek produkcji dochód jest największy?
28. Wyznacz najmniejszą i największą wartość funkcji f(x) = x2 - 4x + 2 w przedziale <- 1, 3〉.
29. Sadownik ma 800 metrów siatki, którą chce ogrodzić działkę w kształcie prostokąta. Doradź sadownikowi, jakie wymiary powinna mieć ta działka, aby jej pole było największe.
30. Wyznacz taką liczbę, aby różnica między nią i jej kwadratem była jak największa.
31. Ogród w kształcie prostokąta, w którym jeden bok jest o l0m dłuższy od drugiego, należy ogrodzić siatką. Oblicz długość siatki, jeśli pole ogrodu wynosi 1200m2.
32. Badamy położenie poruszającego się ciała względem obserwatora. Odległość ciała (w metrach) podana jako funkcja czasu t (w sekundach) wyraża się wzorem y(t) = t2 + 6t + 10. Wyznacz położenia ciała w 4 i 7 sekundzie oraz średnią prędkość między czwartą a siódmą sekundą.
34. Suma kwadratów trzech kolejnych liczb parzystych wynosi 56. Wyznacz te liczby.
35. Wyznacz zbiór wartości funkcji f(x) = x2 - 5x + 6 określonej na przedziale <-3, l〉.
36. Z wysokości 10m wystrzelono strzałę z łuku pionowo do góry z prędkością początkową 50m/s. Wysokość położenia strzały nad ziemią H (w metrach) zmienia się w zależności od czasu t (w sekundach) zgodnie ze wzorem H = 5 + 50t - 5t2. Po ilu sekundach strzała osiągnie maksymalną wysokość i ile ona będzie wynosiła?
37. Suma długości boku trójkąta i wysokości opuszczonej na ten boku wynosi 100cm. Jaką długość powinien mieć bok, a jaką wysokość, aby pole trójkąta było największe?
39. Sporządź wykres funkcji f(x) = x|x|.
41. Jaki znak ma iloczyn współczynników a i b trójmianu kwadratowego y = ax2 + bx + c, jeżeli wiadomo, że odcięta wierzchołka wykresu tego trójmianu wynosi xw = - 2,3?
42. Do wykresu trójmianu kwadratowego y = - 2x2 + bx + c należą punkty A = (0, 1), B = (2, - 1). Wyznacz współczynniki b i c tego trójmianu.
45. Oblicz współczynniki trójmianu kwadratowego, jeśli do jego wykresu należy punkt A = (3, 0) oraz wiadomo, że funkcja osiąga wartość największą y = 12 dla x = 1.
47. Rozwiąż graficznie nierówność x2 - 4x > 2x - 5.
48. Wyznacz współczynnik c trójmianu kwadratowego y = ax2 + bx + c, jeśli wiadomo, że liczba -b/a jest pierwiastkiem tego trójmianu.
49. W trójkąt równoramienny o podstawie długości a = 12cm i wysokości opuszczonej na tę podstawę długości h = 12cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na podstawie trójkąta, a dwa pozostałe na jego ramionach, po jednym na każdym. Jakie powinny być wymiary prostokąta, aby jego pole było największe?
50. Dla funkcji danej wzorem f(x) = - x2 + 4 wyznacz w przedziale <- 2, 3〉 wartość najmniejszą i największą.
52. Który współczynnik trójmianu kwadratowego jest wyznaczony jednoznacznie przez warunek, że oś OY jest osią symetrii wykresu tego trójmianu, a który, że jego wykres przechodzi przez początek układu współrzędnych? Uzasadnij!
53. Oblicz miejsca zerowe i podaj postać iloczynową trójmianu y = - (x - 1)2 + 4.
54. Zbiorem argumentów, dla których funkcja f(x) = x2 + bc + c przyjmuje wartości ujemne jest przedział (1, 3). Oblicz b i c.
55. Dla jakich wartości parametru m nierówność (m - 1)x2 - mx + m<0 jest prawdziwa dla każdego m∈R?
57. Trójmian kwadratowy y = 2x2 - x zapisz w postaci kanonicznej.
59. Wykonaj wykres funkcji y = |x2 - 4x + 3|.
60. Rozwiąż równania:
x2 - |5x - 6| = 0
x2 + |x - 6| = 0
2x2 - 7|x| - 4 = 0
x2 + |x| - 8 = 0
|x2 - 5x| + 6 = 0
61. Rozwiąż nierówności:
|x2 - 3x - 1|<3
|x2 - 6|>5
x2 - |5x - 6|>0
|x2 - 3x - 4|
x + 1
62. Naszkicuj wykresy funkcji:
f(x) = |4x2 - 9|
f(x) = |x2 - 4x - 5| + 2
f(x) = x2 - 6|x| - 7
f(x) = 2x2 - |4x + 6|
f(x) = |2x + 4| - x2
f(x) = |x2 - 2x| + 5
63. Rozwiąż graficznie i algebraicznie układ równań
65. Rozwiąż algebraicznie układ równań
.
Wykonaj wykres funkcji f(x) = x2 + 2x. Podaj równanie paraboli symetrycznej do wykresu funkcji f względem osi OY.
Wyznacz wszystkie liczby całkowite spełniające układ nierówności
.
Znajdź trzy kolejne liczby parzyste dodatnie tak, aby suma kwadratów dwóch mniejszych liczb była równa kwadratowi trzeciej liczby.
Zbadaj algebraicznie, ile punktów wspólnych ma prosta o równaniu x - 2y = 0 z parabolą o równaniu
y = x2 - 2x.Znajdź wszystkie trójmiany kwadratowe, których pierwiastkami są liczby 3 i - 4.
Określ dziedzinę funkcji y =
Dla jakich wartości a∈R najmniejsza wartość funkcji f(x) = x2 - ax + 2 jest większa od najmniejszej wartości funkcji g(x) = x2 - x + a + 1 ?
Znajdź najmniejszą wartość funkcji f(x) =
Dana jest funkcja f(x) = x2 - 5x + 6. Narysuj wykres funkcji: f(x + 3) - 2, - f(x), f( - x), |f(x)|, f( |x|). Napisz wzory nowych funkcji oraz omów i nazwij przekształcenia, które należało wykonać.
Wyznacz trójmian kwadratowy y = ax2 + bx + c wiedząc, że jego wykres przechodzi przez punkty
(0, 1), (1, - 2) oraz dla x = 1 osiada swoją najmniejszą wartość. Napisz ten trójmian w postaci kanonicznej i iloczynowej.Wyznacz parametr m∈R tak aby prosta mx + (2m - 1)y + 3 = 0 była:
a) prostopadła do prostej 2x - 3y + 1 = 0
b) równoległa do prostej - 4x + my + 1 = 0Omów wykres trójmianu kwadratowego f(x} = a(x - p)2 + q w zależności od parametrów a, p, q. Naszkicuj wykres funkcji y = x2 - 7x + 10.
Dana jest funkcja f(x) = (x - a)2 [a(x - a) - a - l]
dla a = 2 rozwiąż równanie f(x) = 2
dla a = −1 rozwiąż nierówność f(x)< - l
87. Dana jest funkcja postaci f(x) = (m - 2)x2 + 2mx + 4m − 1.
Wyznacz zbiór wartości funkcji f wiedząc, że prosta o równaniu x = −2 jest osią symetrii, jej wykresu
VII Wielomiany
Wykonaj działania i uprość wyrażenia:
Wyznacz ze wzoru zmienną g:
Ze wzoru
wyznacz n.Ze wzoru
wyznacz m1.Dla jakich wartości liczb a i b zachodzi równość wielomianów (ax + 2)(x2 + b) = 2(x3 + x2 + x + 1)?
Wykonaj działania i uporządkuj wyrażenia H(x) = W(x) + G(x) (x - 2) jeżeli W(x) = (4x2 - 1)(x + 1),
G(x) = - 4x3 + 9x2 - x - 2.Rozłóż wielomian na czynniki W(x) = x4 - 10x2 + 9.
Napisz wielomian najniższego stopnia o współczynnikach całkowitych, którego jedynymi pierwiastkami są liczby
.Rozłóż wielomian W(x) = 2x3 - 5x2 - x + 6 i P(x) = x4 - 7x - 8 na czynniki liniowe.
Rozwiąż równania:
x3 - x = 80x
x3 - 100x = x2 - 100
2x4 - x3 + 4x - 2 = 0
Dla jakich wartości m wielomian W(x) = (x - 1)(x - 2)(x + m - 3) ma dwa różne miejsca zerowe?
Wykaż, że funkcja f(x) = x3 + 2x2 + 4x - 2 ma dokładnie jedno miejsce zerowe.
Wykonaj dzielenie wielomianu W(x) = x4 - 3x3 + 7x2 - 7x + 6 przez wielomian P(x) = (x - 1)2 + 2.
Wielomian W(x) = x3 + x2 + kx + 1 jest podzielny przez x + 1. Wyznacz parametr k.
Dla jakich wartości parametrów m i n wielomian W(x) = x3 + x2 + mx + n jest podzielny przez wielomian P(x) = (x - 1)(x + 1).?
Przy dzieleniu wielomianu W(x) przez wielomian Q(x) = x2 - x + 2 otrzymuje się dwumian P(x) = 4x - 4 i resztę R(x) = - 13x + 10.
Oblicz pierwiastki wielomianu W(x).
Dla jakich wartości parametru m wyrażenie W(x) + x - m ma dwa różne miejsca zerowe.
Wiedząc, że pierwiastkami wielomianu W(x) = x3 + ax2 są liczby 2 i - 3 wyznacz parametry a i b oraz trzeci pierwiastek.
Dla jakich wartości parametru m, a, b wielomianu W(x) = (x + 2)2(x - m) i Q(x) = x3 + x2 + ax + b są równe.
Współczynniki a, b, c, d wielomianu W(x)ax3 - bx2 - cx + d tworzą w podanej kolejności ciąg arytmetyczny o różnicy r. Wykaż, że liczba 1 jest pierwiastkiem tego wielomianu. Ile pierwiastków ma ten wielomian, jeśli wiadomo, że
Sprawdź przez który z dwumianów x - 1, x + 1 podzielny jest wielomian W(x) = 8x4 + 17x3 - 3x2 + 2x - 24.
Dla jakich wartości parametrów a i b liczba 2 jest dwukrotnym pierwiastkiem wielomianu W(x) = x3 + 4x2 + ax + b?
Dla jakich wartości a, b, c wielomian W(x) = x3 + ax2 + bx + c jest podzielny przez każdy z dwumianów: x - 1, x + 2, x - 3?
Jednym z pierwiastków wielomianu W(x) = x4 - 6x2 - 8x - 3 jest liczba −1. Zbadaj krotność tego pierwiastka.
Dwie kolejne liczby naturalne mają tę własność, że różnica ich sześcianów równa się 91. Jakie to liczby?
Suma sześcianów dwóch kolejnych liczb całkowitych jest równa 216. Jakie to liczby?
Dana jest funkcja f(x) = x3 - (m - 2)x + 2
dla m = 1 rozwiązać równanie f(x) = 8(x + 1)
zbadaj liczbę pierwiastków równania f(x) = 0 w zależności od parametru m.
Wykaż, że dla dowolnego n
N wartość wyrażenia
jest liczbą naturalną.
VIII Funkcje wymierne
Wyrażenie
dla x
, doprowadź do najprostszej postaci.Wyznacz dziedzinę funkcji
.Określ dziedzinę funkcji
.Wyznacz dziedzinę funkcji
.Wyznacz zbiór wartości funkcji
określonej na przedziale <2, 3〉.Dana jest funkcja
. Określ jej dziedzinę i uporządkuj liczby f( - 100), f(0), f(10), f(100) od najmniejszej do największej.Narysuj wykres i podaj przedziały monotoniczności funkcji
.Narysuj wykres funkcji
i podaj liczbę rozwiązań równania f(x) = m w zależności od parametru m.Rozwiąż układ równań
i przedstaw jego interpretację geometryczną.Rozwiąż równanie
Rozwiąż równanie
Rozwiąż równanie
Rozwiąż nierówność
Rozwiąż graficznie nierówność
Wyznacz najmniejszą liczbę całkowitą spełniającą nierówność
Rozwiąż nierówność
Rozwiąż nierówność
Znajdź punkty przecięcia hiperboli y =
z parabolą y = x2 + x + 1.Jakie liczby rzeczywiste spełniają warunek: „suma pewnej liczby i jej odwrotności jest mniejsza od 2”?
Jeżeli odejmiemy od danej liczby jej odwrotność, to otrzymamy
. Jaka to liczba?
IX CIĄGI
1. Które z wyrazów ciągu (an) są równe 0, jeśli
?
2. Wyraz ogólny ciągu arytmetycznego ma postać
. Określ rodzaj monotoniczności tego ciągu.
Wykaż, że ciąg o wyrazie ogólnym an = 3n + 1 jest ciągiem geometrycznym. Podaj jego pierwszy wyraz i iloraz.
Zbadaj na podstawie monotoniczność ciągu określonego wzorem an = n2 - n + 1.
Niech x1, x2 oznaczają pierwiastki równania x2 - 13x + 9 = 0. Uzasadnij, że ciąg (x1, 3, x2) jest geometryczny.
Zbadaj monotoniczność ciągu
Suma trzech początkowych wyrazów ciągu arytmetycznego wynosi 26. Wyznacz drugi wyraz tego ciągu.
Wyznacz ciąg arytmetyczny, w którym piąty wyraz jest równy 19, a czwarty jest pięć razy większy od pierwszego.
Ciąg (an) określony jest rekurencyjnie w następujący sposób
. Wyznacz wzór na n - ty wyraz tego ciągu oraz zbadaj jego monotoniczność.
10. Ciąg określony jest wzorem
. Które wyrazy tego ciągu różnią się od liczby 2 o mniej niż 0,1?
Oblicz ile wyrazów ciągu an = n2 - 102n + 200 jest ujemnych.
Ciąg liczb „trójkątnych" jest zdefiniowany rekurencyjnie
Wyznacz sześć początkowych wyrazów tego ciągu.
Zbadaj monotoniczność ciągu (an), w którym a1 = l, an + 1 = an + n2 + 2n + l.
Ile wyrazów ciągu
jest mniejszych od 15?
15. Dany jest ciąg
. Zbadaj, czy jest on ciągiem arytmetycznym?
Piąty wyraz ciągu arytmetycznego jest równy 4. Jaka powinna być różnica tego ciągu, by suma kwadratów drugiego i szóstego wyrazu była najmniejsza?
Wyznacz liczby x, y wiedząc, że x + y = 8 oraz to, że liczby x, y, 19 w podanej kolejności tworzą ciąg arytmetyczny.
Rozwiąż w liczbach naturalnych równanie - 3 + 1 + 5 + 9 + .. . + (4n - 7) = 375
Oblicz sumę stu pierwszych wyrazów ciągu arytmetycznego - 100, - 97, - 94...
Wyznacz różnicę ciągu arytmetycznego , w którym suma siódmego i jedenastego wyrazu ciągu wynosi 10, a suma piątego i dziesiątego wyrazu jest równa 1.
Wyznacz dodatnią liczbę x tak, aby ciąg (31997, 32001, x) był geometryczny.
W ciągu geometrycznym, w którym wszystkie wyrazy są dodatnie, mamy S2 = 4, S3 = 13. Oblicz S5.
W kwadrat o boku długości a wpisano koło, następnie w to koło wpisano kwadrat, w kwadrat koło itd. Wykaż, że pola kolejnych kół tworzą ciąg geometryczny i oblicz jego sumę.
W ciągu geometrycznym trzeci wyraz jest równy 0,5, a suma dwóch pierwszych wyrazów wynosi 6. Oblicz iloraz tego ciągu.
Dla jakiej wartości parametru m liczby m, 4m - 2, 9m w podanej kolejności tworzą ciąg geometryczny?
Suma trzech liczb tworzących ciąg geometryczny jest równa 7, a ich iloczyn jest równy 8. Wyznacz ten ciąg.
Wyznacz dodatnie liczby x, y wiedząc, że liczby 2, x, y tworzą ciąg geometryczny o ilorazie różnym od 0, natomiast liczby (2, x + l, y) tworzą ciąg arytmetyczny.
Rozwiąż nierówność x2 + x3 + x4 + ...> - l - x , w której lewa strona jest sumą nieskończonego ciągu geometrycznego zbieżnego.
Oblicz wartość wyrażenia (x1 + x2) + ( x1 + x2)2 + ( x1 + x2)3... będącego sumą nieskończonego ciągu geometrycznego, jeśli wiadomo, że
i
są miejscami zerowymi funkcji f(x) = 4x
- x - 12.Zamień na ułamek zwykły liczbę 0,3(21).
31. Wyznacz zbiór wszystkich liczb x, dla których istnieje suma
32. Oblicz sumę wyrazów nieskończonego ciągu geometrycznego zbieżnego, w którym drugi wyraz jest równy
, a trzeci wyraz
.
33. Oblicz sumę szeregu geometrycznego, którego pierwszy wyraz wynosi
a drugi
34. Suma nieskończonego ciągu geometrycznego jest trzy razy większa od jego pierwszego wyrazu. Wyznacz iloraz tego ciągu.
35. Liczbę 2
+ 2 przedstaw w postaci sumy szeregu geometrycznego o danym ilorazie równym
36. Rozwiąż równanie 0,01x + 0,0001x + 0,000001x + … =
, gdzie lewa strona jest sumą szeregu geometrycznego zbieżnego.
37. Oblicz iloraz nieskończonego ciągu geometrycznego zbieżnego wiedząc, że jego suma wynosi 9, a drugi wyraz jest równy 2.
38. Oblicz sumę 1 -
39. Liczbę 2,0(36) zamień na ułamek zwykły.
40. Dla jakich x szereg geometryczny
jest zbieżny?
41. Rozwiąż równanie a + x + x2 + x3 + … = 4x, gdzie lewa strona jest sumą nieskończonego ciągu geometrycznego.
42. Dana jest funkcja
+ …, gdzie prawa strona jest sumą wyrazów nieskończonego ciągu geometrycznego zbieżnego. Znajdź dziedzinę tej funkcji.
43. Zbadaj monotoniczność i zbieżność funkcji:
a)
b)
44. Ciągi (an) i (bn) są zbieżne oraz
i
Oblicz
.
45. Oblicz
jeśli an = 3n + 4.
46. Oblicz granicę
,
.
Miary trzech kolejnych kątów czworokąta wpisanego w koło tworzą ciąg arytmetyczny o różnicy 47°. Oblicz miary kątów tego czworokąta.
Kiedy cesarz Karol odwiedził Norymbergę miasto podarowało mu puchar, w którym znajdowało się 100 sztuk złota. Pierwsza z nich miała wartość jednego dukata, druga - dwóch, trzecia - trzech, itd. Aż do setnej mającej wartość 100 dukatów. Jaką wartość przedstawiał dar nie licząc pucharu?
Piłka odbijając się od ziemi osiągnęła za każdym razem wysokość wynoszącą 2/3 poprzedniej. Jak wysoko wzniosła się piłka po pierwszym uderzeniu, jeśli po szóstym odbiła się na wysokość 32cm?
Koszt robót przy drążeniu szybu wiertniczego przedstawia się następująco: odwiert pierwszego metra szybu kosztuje a zł, każdego następnego o b zł drożej w stosunku do kosztu robót za poprzedni metr. Jaki jest całkowity koszt budowy tego szybu, jeśli ma on 40 metrów głębokości?
Przypuśćmy, że bibułkę o grubości 1/16 mm składamy na pół, jeszcze raz na pół, i tak dalej, i że moglibyśmy tak ją złożyć 10 razy. Jaka byłaby wtedy grubość warstwy złożonej w ten sposób bibułki?
Swobodnie spadające ciało w ciągu pierwszej sekundy przebywa o 4,9m więcej niż w poprzedniej. Jaką odległość pokona ciało w ciągu 12 sekund?
Troje dzieci pani Kowalskiej rodziło się dokładnie co dwa lata. Średnia arytmetyczna wieku dzieci w x lat po urodzeniu najstarszego dziecka wynosi f(x). Naszkicuj wykres tej funkcji dla x
<0,10>.Ile uderzeń w ciągu doby wykona zegar, który wybija tylko pełne godziny?
Po roku młode drzewko wypuściło pierwszą boczną gałązkę. Każda gałązka mająca co najmniej dwa lata wypuszcza co roku boczny pęd. Ile wszystkich gałęzi będzie miało drzewko po 1,2,3,4,5 latach? Oznaczmy przez un liczbę wszystkich rozgałęzień rozgałęzień - letniego drzewka. Podaj wzór rekurencyjny na un.
Dany jest skończony i uporządkowany zbiór kwadratów, których poła powierzchni tworzą ciąg arytmetyczny. Pole powierzchni pierwszego z nich jest równe 12cm2, a piątego 30cm2. Ile jest kwadratów, jeśli suma ich pól równa się polu kwadratu o boku 2lem.
Ktoś wymyślił sensacyjną wiadomość i zakomunikował ją w ciągu godziny trzem osobom. Zakładając, że każda z powiadomionych osób w ciągu godziny poda tę wiadomość trzem osobom, które jej jeszcze nie słyszały, oblicz w przybliżeniu, po jakim czasie liczba osób znających tę wiadomość przekroczy 250000.
Z miast A i B odległych o 119km wyjeżdżają naprzeciw siebie dwaj kolarze, przy czym drugi kolarz startuje w dwie godziny po wyjeździe pierwszego. Pierwszy kolarz przebywa w ciągu pierwszej godziny 20km, a w każdej następnej o 2km mniej niż w poprzedniej. Dragi kolarz przebywa w pierwszej godzinie l0km, a w każdej następnej o 3km więcej niż w poprzedniej. Po ilu godzinach spotkają się kolarze i w jakiej odległości od miasta B?
W ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego równa się 7, a suma kwadratów wyrazów drugiego i czwartego równa się 40.
a. Suma ilu początkowych wyrazów tego ciągu równa się - 64?
b. Wykazać, że dla dowolnego ciągu arytmetycznego spełniony jest warunek S3m = 3(S2m - Sm).
60. Dany jest nieskończony zbieżny ciąg geometryczny x, 1, ...
a. Dla jakich wartości x pierwszy, drugi i czwarty wyraz ciągu tworzą trzy kolejne wyrazy ciągu arytmetycznego.
b. Dla jakich wartości x trzeci i czwarty wyraz tego ciągu są sinusem i cosinusem tego samego kąta.
c. Naszkicuj wykres funkcji f gdzie f(x) jest sumą wszystkich wyrazów tego ciągu.
61. Dany jest nieskończony ciąg geometryczny x, x(3 - x2), x(3 - x2)2, ...
a. Dla jakich wartości x istnieje suma wyrazów tego ciągu? Oblicz te sumę.
b. Dla jakich wartości x spełniona jest nierówność x + x(3 - x2) + x(3 - x2)2 + …<
c. Dla jakich (90°,180°) liczba 1,5 jest pierwiastkiem równania
x + x(3 - x2) + x(3 - x2 )2 + ... = 6 sin2
+ 4 cos2
+ 3 sin
.
62. Suma czterech początkowych wyrazów rosnącego ciągu arytmetycznego (an) równa się 13
. Iloczyn pierwszego i trzeciego wyrazu tego ciągu jest równy 1
.
a. Oblicz wyraz pierwszy pierwszego różnicę tego ciągu.
b. Dla jakich n
N suma pierwszego początkowych wyrazów tego ciągu nie jest większa od 136?
c. Dla jakich pierwszego ciąg (bn) określony wzorem
jest zbieżny do liczby 3,5?
63. W ciągu arytmetycznym (an) wyraz pierwszy a1 = - 21 a różnica r = 3.
a. Dla jakiej wartości n stosunek
równa się - 5 ?
b. Dla jakiego n suma n początkowych wyrazów tego ciągu jest większa od - 75?
c. W ciągu geometrycznym (bn) I ilorazie q wyraz b1 = 3. Dla jakich wartości q piąty wyraz ciągu geometrycznego jest równy dwunastemu wyrazowi danego ciągu arytmetycznego?
64. W ciągu arytmetycznym wyraz ogólny an = - 4n + 20.
a. Dla jakich n spełnione jest równanie 7an = Sn + 20?
b. Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu podzielnych przez 6.
c. Ile wyrazów tego ciągu należy do przedziału < - 120,120>?
65. Dany jest ciąg o wyrazie ogólnym
a. Dla k = 3 wyznacz granicę ciągu bn określonego wzorem bn =
b. Dla jakich wartości k ciąg an jest rosnący?
c. Trzeci dziesiąty wyraz ciągu an oraz liczba 11,75 wzięte w tej kolejności tworzą ciąg arytmetyczny. Wyznaczyć k.
66. Wyrazy ciągu arytmetycznego (an) spełniają warunki a2 + a4 = 8, a7 = 16.
a. Wyznaczyć wyraz ogólny tego ciągu.
b. Wiadomo, że wyrazy ak, ak + 1, ak + 1 ciąg (an) wzięte w tej kolejności są trzema kolejnymi wyrazami pewnego ciągu geometrycznego. Wyznaczyć k.
c. Sumy częściowe S8 i Sn tego ciągu spełniają warunek Sn - S8 = 140. Wyznaczyć n.
67. Dany jest ciąg (an) o wyrazie ogólnym an = 5 + (n - 1)(k - k2), gdzie k jest parametrem.
a. Wykazać, że ciąg (an) jest ciągiem arytmetycznym. Dla jakich k jest on malejący?
b. Dla k = 2 obliczyć sumę wyrazów od dwudziestego do trzydziestego.
c. Wiadomo, że liczba wyrazów ciągu (an) jest równa 100 i k = 1/2. Dla jakiej wartości m stosunek wyrazu stojącego na m miejscu od początku do wyrazu stojącego na m miejscu od końca jest równy 30/109?
68. Suma n początkowych wyrazów ciągu (an) określona jest wzorem Sn = n2 - 14n.
a. Oblicz trzydziesty pierwszy wyraz ciągu.
b. Na podstawie definicji wykazać, że (an) jest ciągiem arytmetycznym.
c. Wyznaczyć trzy kolejne wyrazy ciągu spełniające warunek: kwadrat środkowego wyrazu jest o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
X Planimetria
Dane są dwa odcinki o długościach 1 i a. Korzystając z twierdzenia Talesa skonstruuj odcinek o długości
a) a2 b)
Skonstruuj trójkąt równoramienny o podstawie długości 4cm i kącie między ramionami 30°.
Skonstruuj czworokąt o kolejnych bokach długości 2cm, (2 + 4
)cm, (2 + 2
)cm, 2cm i kącie 60° miedz; krótszymi bokami. Czy w ten czworokąt można wpisać okrąg? Odpowiedź uzasadnij.Punkt M dzieli średnicę AB okręgu na odcinki o długościach 4cm i 9cm. Oblicz długość cięciwy przechodzące przez punkt M i prostopadłej do AB.
Dwa boki trójkąta mają długości
i 5
, a kąt przeciwległy krótszemu z nich ma miarę 45°. Oblicz długość trzeciego boku trójkąta.Fotografia 12cmxl8cm ma ramkę o szerokości a. Wyznacz tę szerokość, jeśli pole ramki jest równe polu fotografii.
Krótsza przekątna dzieli trapez prostokątny na dwa trójkąty, z których jeden jest równoboczny. Wysokość trapezu jest równa 6
cm. Oblicz pole tego trapezu.Długości boków prostokąta są równe 2cm i 5cm. Oblicz długości boków prostokąta, podobnego do danego, o obwodzie 56cm.
Na jednym z ramion kata o wierzchołku A odłożono odcinki AB i AC o długościach odpowiednio 5
i 16, a na drugim odcinki AD i AF o długościach odpowiednio 8 i 10. Zbadaj czy trójkąty ACD i AFB są podobne.Pole trójkąta prostokątnego równoramiennego jest proporcjonalne do kwadratu przeciwprostokątnej. Znajdź współczynnik proporcjonalności.
Pięciokąt ABCDE ma obwód 15, a pole 32, natomiast pięciokąt KLMNP ma obwód 30, a pole 120. Czy te pięciokąty mogą być podobne?
Wysokość trapezu równoramiennego wynosi 5cm, a jego przekątna 13cm długości. Oblicz pole tego trapezu.
Oblicz długość dłuższej przekątnej równoległoboku , w którym boki mają długość 4cm i 6cm, a miara kąta między nimi 60°.
Dany jest trapez prostokątny ABCD, w którym |
|
i |AB|>|CD|. Wiedząc, że przekątne mają długości 13 i
, a różnica długości podstaw równa się 8, oblicz obwód trapezu. Czy w ten trapez można wpisać okrąg? Uzasadnij.Oblicz obwód rombu wiedząc, że jego pole wynosi 24cm , a krótsza przekątna ma długość 6 cm.
Oblicz pole trójkąta ABC mając dane |AB| = 4, |
= 30°, |
B| = 45°.W trójkącie prostokątnym długości przyprostokątnych wynoszą 8 i 15. Oblicz długość środkowej poprowadzonej z wierzchołka kąta prostego.
W trapezie równoramiennym opisanym na okręgu, ramiona maja po 6cm długości, a jedna z podstaw jest dwa razy większa od drogiej. Oblicz długości podstaw tego trapezu.
W okrąg wpisano czworokąt ABCD, którego miary kątów przy wierzchołkach A, B, C mają się do siebie jak 5:7:9. Znajdź miarę kata przy wierzchołku D.
W trójkącie ABC połączono środki boków, otrzymując trójkąt KLM. Obwód trójkąta KLM jest o 20cm mniejszy od obwodu trójkąta ABC. Oblicz obwód trójkąta ABC.
Dwa boki trójkąta mają długość 1cm i 4cm. Oblicz obwód tego trójkąta, jeżeli wiadomo, że długość trzeciego boku wyraża się liczbą naturalną.
Na okręgu o promieniu r = 2cm opisano trapez równoramienny o ramieniu długości 5cm. Oblicz pole trapezu.
Obwód trapezu opisanego na okręgu wynosi 30cm. Jedno z jego ramion jest dwa razy dłuższe od drugiego ramienia. Oblicz długości ramion trapezu.
W okrąg wpisano czworokąt ABCD, w którym miary kątów przy wierzchołkach A i B wynoszą odpowiednio 65° i 97°. Oblicz miary kątów przy wierzchołkach C i D.
Symetralna przeciwprostokątnej trójkąta prostokątnego dzieli jedną z przyprostokątnych na odcinki o długościach 4cm i 5cm. Oblicz długości boków tego trójkąta. Liczby 2a - 2, 2a + 2, a + 1 są długościami boków trójkąta. Do jakiego przedziału liczbowego należy liczba a?
Dany jest okrąg o środku O i promieniu r. Który z trójkątów OAB, gdzie A i B są punktami należącymi do okręgu, ma największe pole?
W trójkącie ABC na boku BC obrano w ten sposób punkt D, że cosinus kąta BAD jest równy 0,3, a cosinus kąta DAC wynosi
. Oblicz pole trójkąta ABC wiedząc, że |AB| = 5 i |AC| = 6.Dwa wielokąty wypukłe mają razem 24 boki i 117 przekątnych. Ile wierzchołków ma każdy z tych wielokątów?
Jeżeli połączymy środki sąsiednich boków sześciokąta foremnego o polu 8, to otrzymamy nowy sześciokąt. Oblicz jego pole.
Wielokąt foremny ma 54 przekątne. Ile ma boków?
W równoległoboku ABCD przekątne AC i BD mają odpowiednio długości 4cm i 6cm oraz tworzą kąt o mierze 60°. Oblicz długości boków równoległoboku.
W trójkącie ABC o obwodzie 104, dwusieczna kata A dzieli kat BC na odcinki |BD| = 15 i |DC| = 25. Oblicz długości boków trójkąta ABC.
Pole trójkąta prostokątnego wynosi 150, a przeciwprostokątna ma długość 25. W jakim stosunku dzieli tę przeciwprostokątną wysokość opuszczona z wierzchołka kata prostego?
Dana jest prostokątna kartka papieru o wymiarach 30cm i 40cm. Jeśli odetniemy od każdego brzegu jednakowej szerokości paski papieru, to otrzymamy kartkę o powierzchni o połowę mniejszej od danej kartki. Jakiej szerokości pasek odcięliśmy?
W trójkącie prostokątnym ABC wysokość opuszczona z wierzchołka kąta prostego dzieli przeciwprostokątną AB na odcinki równe 2 i 3. Oblicz pole tego trójkąta.
Mając dane R - długość promienia okręgu opisanego na trójkącie oraz miary
i
dwóch kątów w trójkącie, oblicz pole trójkąta.Dana jest długość p dłuższej przekątnej równoległoboku oraz miary kątów
i
, jakie tworzy ona z bokami równoległoboku. Oblicz długości boków tego równoległoboku.Jaką długość może mieć trzeci bok trójkąta rozwartokątnego, jeśli dwa krótsze boki mają długości 5
i 12?Długości boków trójkąta wynoszą 7cm i 8 cm, a kąt między nimi 150°. Oblicz długość wysokości opuszczonej na prostą zawierającą najkrótszy bok.
Kwadrat i trójkąt równoboczny mają te same pola. Wyznacz stosunek ich obwodów.
41. Uzasadnij wzór na pole trójkąta
gdzie
i
są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość o długości h.
42. Dwa boki trójkąta mają długość 8cm i 16cm, a kąt między nimi 60°. Wyznacz długość trzeciego boku i miary pozostałych kątów.
Wysokość trójkąta jest o 6cm dłuższa od boku, do którego została poprowadzona. Oblicz długość tego boku, jeśli pole trójkąta wynosi 140cm2
Oblicz miarę największego kąta w trójkącie o bokach 3, 5 i 7.
Oblicz promień okręgu wpisanego w trójkąt o bokach 6, 5, 5.
Na kole o promieniu r opisano trójkąt prostokątny, którego przyprostokątne mają długości x i y. Wyznacz y jako funkcję x i podaj jej dziedzinę.
Pole prostokąta wynosi 120cm2 a jego przekątna ma długość 17cm. Oblicz długości boków prostokąta.
Obwód trójkąta jest równy 500cm, a jego pole 500cm2. Oblicz długość promienia okręgu wpisanego w ten trójkąt.
W trójkącie ABC połączono odcinkami środki boków i okazało się, że otrzymany trójkąt ma obwód o 14cm mniejszy od obwodu danego trójkąta. Oblicz obwód trójkąta ABC.
Dwusieczna kąta przy podstawie trójkąta równoramiennego tworzy z przeciwległym bokiem kąt 75°. Znajdź miary kątów tego trójkąta.
W trójkącie ABC:
A = 135°, |AC| =
, |AB| = 7. Wyznacz długość boku BC.Długości odpowiednich boków dwóch podobnych wielokątów wynoszą 5 i 15, a różnica ich obwodów wynos 80. Oblicz obwody tych wielokątów.
Na okręgu opisano trapez, którego obwód wynosi 52cm. Oblicz długość odcinka łączącego środki ramion trapezu.
Dwa boki trójkąta maja długości 1cm i 5cm. Oblicz obwód tego trójkąta, jeśli wiadomo, że długość trzeciego boku wyraża się liczbą naturalną.
W trapezie równoramiennym krótsza podstawa ma długość 12cm, a opuszczona z wierzchołka kata rozwartego wysokość dzieli jedną z przekątnych w stosunku 2:3. W jakim stosunku dzieli ta wysokość dłuższą postawę trapezu.
Podstawa trójkąta równoramiennego wynosi 6, a długość ramion jest równa 5. W jakiej odległości od podstaw znajduje się punkt przecięcia wysokości tego trójkąta?
Oblicz pole trójkąta prostokątnego, w którym przeciwprostokątna ma długość 37cm, a suma długość przyprostokątnych wynosi 47cm.
Dany jest trójkąt o bokach długości 4cm, 5cm i 8cm. Rozstrzygnij czy jest to trójkąt ostrokątny, prostokątny; czy rozwartokątny.
Oblicz miary kątów trójkąta, w którym wysokość i środkowa poprowadzone z jednego wierzchołka dzielą kąt przy tym wierzchołku na trzy równe części.
Wyznacz długości przekątnych rombu, którego bok ma długość a i kąt ostry ma miarę
.Plac zabaw w kształcie trapezu równoramiennego podzielono murkiem wzdłuż przekątnej. Oblicz długość tego murku, jeśli wiadomo, że najdłuższy bok placu ma 16m, bok do niego przyległy 6m, a kąt między nimi zawarty 60°.
W trójkącie prostokątnym o bokach długości 6, 8 i 10 wyznacz długość najdłuższej środkowej.
Dwa krótsze boki trójkąta rozwartokątnego mają długości 5 i 7. Jaką długość może mieć trzeci bok?
Przyprostokątne trójkąta prostokątnego mają długości 3 i 6. Oblicz długość odcinka dwusiecznej kąta prostego, zawartego w trójkącie.
Oblicz pole trapezu o długościach podstaw 12 i 3 wiedząc, że można na nim opisać okrąg i w niego wpisać okrąg.
Oblicz pole trójkąta równoramiennego o obwodzie 20, którego kat przy podstawie ma miarę 30°.
Oblicz pole trójkąta, w którym dwa kąty maja miarę 30° i 45° oraz promień okręgu opisanego na trójkącie ma długość 24cm.
Odległość środków dwóch okręgów stycznych wewnętrznie wynosi 6, a mniejszy okrąg dzieli odcinek łączący środki obu okręgów na połowy. Znajdź promienie tych okręgów.
Okrągły obrus o średnicy 150 cm obszyto ozdobną taśmą. Ile metrów bieżących taśmy należy kupić na obszycie pięciu takich obrusów?
Dwa promienie okręgu tworzą kąt 54°. Ile stopni ma kąt między stycznymi do okręgu poprowadzonymi w końcach tych promieni?
Jaka jest skala podobieństwa dwóch kół o promieniach równych 6cm i l0cm?
Pizza ma średnicę 30cm, ale pieczarkami pokryta jest tylko środkowa jej część o promieniu 12cm. Jaki procent pizzy pokryty jest pieczarkami?
Dane są okręgi o1(A, r) i o2(B, R) oraz r = 3k + l, R = 2k + 3, |AB| = 6k - 3. Dla jakiej wartości k okręgi są styczne wewnętrznie, a dla jakiej zewnętrznie?
W okrąg wpisano taki trójkąt ABC, że AB jest średnicą okręgu. Wiedząc, że długość łuku BC stanowi 75 długości okręgu, oblicz miarę kąta ABC.
Znajdź miarę kąta wpisanego w okrąg i opartego na 1/6 okręgu.
Przez punkt położony na okręgu poprowadzono styczną i cięciwę. Znajdź kąt pomiędzy nimi, jeśli cięciwa równa jest co do długości promieniowi.
W okrąg wpisano sześciokąt foremny oraz kwadrat. Obwód sześciokąta wynosi 24. Oblicz pole kwadratu.
Dane są dwa okręgi o(A, r1.) i o(B, r2) takie, że r1 = 3k + l, r2 = 2k + 3, |AB| = 6k - 3. Dla jakich wartości parametru k okręgi te nie mają punktów wspólnych i są położone na zewnątrz siebie?
Dla jakiej wartości k prosta 1 jest styczna do okręgu o(A, r), jeśli wiadomo, że r = 2k - l i odległość punktu A od prostej 1 równa jest 5 - k?
W okrąg, którego promień ma l0cm, wpisano prostokąt. Środki kolejnych boków prostokąta połączono odcinkami. Oblicz obwód otrzymanego czworokąta.
Na okręgu o promieniu 6cm opisano trójkąt równoramienny o kącie między ramionami 120°. Oblicz długość podstawy tego trójkąta.
Cięciwa okręgu jest odległa od środka okręgu o 8cm i jest o 2 cm dłuższa od promienia okręgu. Jaką długość ma promień tego okręgu?
Dwa zewnętrznie styczne okręgi są styczne do ramion kata. Odległość ich środków od wierzchołka kata wynosi odpowiednio 10 i 15. Oblicz długości promieni tych okręgów.
Dane koło o promieniu R podziel okręgiem współśrodkowym na dwie części o równych polach.
Dwa przecinające się okręgi mają promienie R i r (R>r), a odległość środków tych okręgów wynosi a. Oblicz odległość wspólnej cięciwy od środka większego okręgu.
W okrąg o promieniu długości 15cm wpisano trójkąt równoramienny o kącie między ramionami 150°. Oblicz długość podstawy tego trójkąta.
Cięciwa dzieli okrąg w stosunku 1:3. Oblicz stosunek pól figur, na które ta cięciwa podzieliła koło.
Oblicz pole wycinka kołowego, który zakreśli mała wskazówka zegarka od godziny 15.00 do 16.30. Długość wskazówki wynosi 2cm.
Cień drzewa ma 20m, w tym samym czasie cień człowieka o wzroście 180cm ma długość 2,5m. Jaka jest wysokość drzewa?
Czy istnieje wielokąt, który ma 50 przekątnych?
Na brzegu jeziora mieszkało sześciu rybaków (domy żadnych trzech nie zawierały się w jednej prostej). Zimą gdy tafla lodu pokryła jezioro rybacy odwiedzając się nawzajem wydeptywali ścieżki tak, że domy każdych dwóch rybaków były połączone ścieżką wzdłuż linii prostej. Ile było ścieżek?
Na samym brzegu strumienia rosła topola. Wiatr złamał ją na wysokości trzech metrów nad ziemią i topola upadła prostopadle do brzegu strumienia tak, że jej wierzchołek oparł się o drugi brzeg. Strumień ma szerokość czterech metrów. Jak wysoka była topola?
Pan Jan wytyczy na płaskiej działce okrągły klomb o średnicy 7,6m, a na jego terenie założy oczko wodne w kształcie sześciokąta foremnego o najdłuższej przekątnej 2m. Ścieżki zajmą powierzchnię 3m2. Ile, co najmniej, będą kosztować nasiona trawy potrzebne do obsiania tego klombu, jeśli nasiona trawy sprzedawane są w opakowaniach 0,5kg (co wystarcza na obsianie 20m2 powierzchni) po 11,50zł i w opakowaniach l kg po 22zł?
Karol wyszedł na spacer wokół trójkątnej działki leśnej. Wyruszył z punktu A i przeszedł 360m w kierunki północnym, wykonał zwrot w prawo o 120° i przeszedł dalej 960m i po ponownym zwrocie w prawo wrócił do punktu A. Jak długo trwał spacer, jeśli przyjmiemy, że Karol szedł po obwodzie trójkąta ze średnią prędkością 5,4km/h i nie zatrzymywał się?
Żelazny pręt o długości 2m zgięto dokładnie pośrodku tak, że między jego połówkami powstał kąt 120°. Jaka jest odległość między końcami pręta po zgięciu?
W jakiej odległości od punktu startu znalazł się samochód, jeżeli po starcie przebył l00km na północ. 300km na zachód i wreszcie 500 km na południe?
Wyznacz skalę mapy, na której jezioro Śniardwy zajmuje powierzchnię 546cm2. Przyjmijmy, że powierzchnia jeziora Śniardwy w rzeczywistości wynosi 114km2.
Dwa odcinki jednakowej długości są równoległe, ale nie leżą na jednej prostej. Podaj trzy izometrie przekształcające jeden odcinek na drugi.
Znajdź wszystkie liczby k, by przekształcenie F określone wzorem F((x, y)) = ( - ky, x) było izometrią.
XI Geometria analityczna
Dla jakiej wartości parametru n punkty A = (2, 1) B = ( - 3, 2) C = (2n - 1, - n) są wierzchołkami trójkąta prostokątnego o kącie prostym przy wierzchołku A?
Zbadaj czy wektory
i
SA równoległe wiedząc, że
+ [1,5],
= [2,10].Dany jest wektor
= [ - 8,6]. Wyznacz wektor jednostkowy równoległy do
o zwrocie przeciwnym do
.Niech A = ( - 3, 4), B = (2, - 6). Wyznacz współrzędne punktu C tak, aby
=
.Niech A = ( - 4, 3), B = (2, 1), C = (1, - 3). Wyznacz współrzędne punktu D tak, aby wektor
był wektorem przeciwnym do wektora
.Niech
= [ - 2, 5],
= [1, 3]. Oblicz współrzędne i długości wektora 3(2
-
) - 5
.Znajdź wektor o długości 10 prostopadły do wektora
= [3, 4].Kąt między dwoma wektorami
i
jest równy 120o, a długości tych wektorów wynoszą odpowiednio 1 i
. Oblicz długość wektora
-
.Bok kwadratu ABCD ma długość a. Oblicz iloczyn skalarny
o
.Niech
. Uzasadnij, że podwojona suma kwadratów długości wektorów
i
jest równa sumie kwadratów długości wektorów
i
.Oblicz długości boków trójkąta ABC zbudowanego na wektorach
= [ - 3, 2] i
= [5, 1].Punkt O jest środkiem ciężkości trójkąta ABC. Wykaż, że
+
.Wiedząc, że A = (5, 3), B = (3, - 2), C = (3, 5), znajdź kąt między wektorami
i
.Wektory
= [7, 1] i
= [6, - 6] zawierają się odpowiednio w dwóch bokach trójkąta
i
. Oblicz cosinus kąta zawartego między tymi bokami.Oblicz iloczyn skalarny wektorów
jeśli wiadomo, że
.Wektory
i
tworzą kąt
. Wiedząc, że
i
. Oblicz
Dane są wektory
= [ - 3, 2] i
= [4, - 1]. Wyznacz wektor
prostopadły do wektora
i taki, że
= 10.Dane są punkty A = (1, 1) i B = (3, 5). Wyznacz na osi OY taki punkt C, dla którego trójkąt ABC jest trójkątem prostokątnym.
Dane są punkty A = (1, 1) i B = (3, 5). Wyznacz na prostej x - 3y - 6 = 0 taki punkt C, dla którego trójkąt ABC jest trójkątem prostokątnym.
Wyznacz taką wartość m, aby proste k: y = 3x - 5 i l: y = mx - 2y + 9 były równoległe.
Napisz równanie prostej 2x + y - 4 = 0 w postaci odcinkowej
. Podaj a i b. Narysuj tę prostą w układzie współrzędnych.Wyznacz równanie prostej prostopadłej do prostej y =
.Zbadaj, czy prosta o równaniu 4x - y - 3 = 0 jest symetralną odcinka o końcach A = ( - 3, 2) i B = (5, 0).
Dla jakiej wartości parametru p proste o równaniach 3x - 4y + 5 = 0 i (2p + 1)x - y + 3 = 0 są równoległe?
Zbadaj czy punkty A = ( -7, -2), B = ( -3, 1), C = (5, 7) są współliniowe.
Narysuj prostą o równaniu y = 2x - 3. Podaj równanie prostej symetrycznej do niej względem
osi OX
prostej x = 2.
Wyznacz równanie osi symetrii trójkąta równoramiennego o wierzchołkach A = ( -2, -3),
B = ( -1, 2) i C = (4, 1).
Dany jest trójkąt o wierzchołkach A = ( -1, 3), B = (1, -3), C = (5, 5). Wyznacz równanie prostej zawierającej środkową AD tego trójkąta.
Wyznacz te wartości parametru m, dla których prosta y = mx + 5 wraz z osiami układu współrzędnych ogranicza trójkąt o polu 10.
Wyznacz równanie prostej przechodzącej przez punkt K = (3, 3) równoległej do prostej wyznaczonej przez punkty A = ( -1, 4) i B = (1, 1).
Znajdź odległość punktu A = ( -1, 4) i B = (1, 1).
Napisz równania stycznych do okręgu x2 + y2 = 4 i przechodzących przez punkt P = (0, 4).
Znajdź równanie prostej, która przechodzi przez punkt (2, - 3) i jest nachylona do osi OX pod kątem 30o.
34. Na prostej o równaniu y = x - 6 znajdź taki punkt M, żeby kwadrat odległości M od punktu od punktu A = (2, 2) był najmniejszy.
35. Napisz równanie prostej zawierającej wysokość CD trójkąta ABC o wierzchołkach
A = ( - 2, 1), B = (4, 3), C = (1, 4).
36. Zbadaj czy proste o równaniach x + 2y + 8 i
są symetryczne względem prostej o równaniu
y =
.
37. Oblicz odległość między prostymi równoległymi: prostą y = -2 + 1 oraz prostą wyznaczoną przez punkty K = (1, 3) i L = (0, 5).
38. Dla jakich wartości parametru a współczynnik kierunkowy prostej przechodzącej przez punkty
A = ( -5, 0), B = (0, a) należy do przedziału < -1, 1>?
39. Zbadaj wzajemne położenie okręgów o równaniach x2 + y2 - 2x + 6y - 6 = 0 i x2 + y2 - 4x - 5 = 0.
40. Napisz równanie okręgu, którego średnicą jest odcinek prostej x - 2y - 6 = 0 wycięty przez hiperbolę o równaniu x y = 8.
41. Wyznacz równania stycznych do okręgu o równaniu x2 + y2 - 4x - 1 = 0 i prostopadłych do prostej o równaniu 2x - y - 4 = 0.
42. Dla jakich wartości parametru m równanie x2 + y2 + 2mx + 4mx + 5 = 0 przedstawia okrąg?
43. Dla jakich wartości m prosta y = m - x jest rozłączona z okręgiem x2 + y2 - 4x = 0.
44. Podaj interpretację graficzną układu równań
. Ile rozwiązań ma ten układ?
45. Zbadaj wzajemne położenie okręgów x2 + y2 - 2x = 0 i x2 + y2 - 6x = 0.
46. Oblicz pole koła określonego nierównością x2 + y2 - 2x + 4y + 1
0.
47. Wyznacz współrzędne środka i długość promienia okręgu określonego równaniem
x2 + y2 - 2x + 8y + 1 = 0.
48. Podaj interpretację geometryczną układu nierówności
49. Zbadaj, ile punktów wspólnych mają okręgi o równaniach
.
50. Zilustruj w układzie współrzędnych zbiór A
jeśli A = {(x, y):x
, B =
Czy otrzymana figura jest ograniczona? Czy otrzymana figura jest wypukła?
51. Napisz równanie okręgu, którego średnicą jest odcinek AB o końcach A = ( - 1, 3) i B = (1, - 1).
52. Napisz równanie okręgu przechodzącego przez punkt A = (7, 9) i stycznego do osi OX w punkcie B = (4, 0).
53. Mając dane równanie okręgu i równanie prostej zawierającej cięciwę tego okręgu:
oblicz długość cięciwy.
54. Dany jest okrąg o równaniu x2 + y2 = 4. Narysuj okrąg o środku w pierwszej ćwiartce układu współrzędnych i średnicy długości 2
styczny zewnętrznie do danego okręgu w punkcie jego przecięcia z prostą o równaniu x - 3y = 0.
55. Określ wzajemne położenie okręgu o równaniu x2 + y2 = 8 i prostej o równaniu x - y = 4.
56. Suma pól dwóch kół, których okręgi są styczne zewnętrznie wynosi
cm2. Oblicz długość promieni tych okręgów, jeśli odległość tych środków wynosi 12.
57. Odcinek AB jest średnicą okręgu o równaniu: x2 + y2 - 2x + 4y - 4 = 0 i A = (0,2
- 2). Oblicz współrzędne punktu B.
58. Napisz równanie okręgu o środku w punkcie o współrzędnych (3, 4) stycznych do osi OX. Podaj współrzędne punktów przecięcia tego okręgu z prostą o równaniu y = 2.
59. Punkty M = (3, 1), N = (6, 5) są kolejnymi wierzchołkami trapezu KLMN. Stosunek długości podstaw trapezu jest równy 1:2. Dłuższa podstawa trapezu zawiera się w prostej o równaniu 4x - 3y - 8 = 0. Oblicz pole trapezu.
60. Jeden z boków prostokąta ABCD ma długość 2
oraz A = ( - 1, 2), B = (3, 1). Znajdź współrzędne pozostałych wierzchołków tego prostokąta.
61. Oblicz pole czworokąta ABCD, jeżeli A = (0, 0), B = (2, 0), C = (1, 1), D = (2, 3).
62. Sprawdź czy czworokąt ABCD o wierzchołkach A = (2, 4), B = (12, - 4), C = (7, 5), D = (12,1).
63. Dane są punkty A = ( - 4, 1), B = (0, - 2), C = ( - 2, 2), D = (3, - 1), E = (5, 2) i F = (1, 3). Zbadaj czy trójkąt ABC i DEF są przystające.
64. Punkt S = ( - 1, 0,5) jest środkiem równoległoboku ABCD, w którym A = ( - 3, - 3), B = (1, - 1). Oblicz współrzędne pozostałych wierzchołków tego równoległoboku.
65. Punkty A = ( - 4, - 1), B = (2, - 1), C = ( - 3, 4) są wierzchołkami pewnego trójkąta. Oblicz jego pole.
66. Znajdź obraz A'B'C' trójkąta ABC, gdzie A = ( - 2, 3), B = (0, - 1), C = (2, 1) w jednokładności o skali - 2
i środku w punkcie (0,0). Jaką figurą jest czworokąt AC'A'C?
67. Wyznacz współrzędne punktu P, którego obrazem w jednokładności o środku S = ( - 1, 4) i skali
k = 3 jest punkt P' = (5, 3).
68. Wyznacz współrzędne obrazu punktu A w jednokładności o środku w punkcie (0,0) i skali k =
.
69. Prosta 1 przechodzi przez punkty A = ( - 3, 3) i B = (1, 1). Napisz równanie, która jest obrazem prostej 1 w jednokładności o środku O = (0, 0) i skali k = 2.
70. W czworokącie ABCD dane są: A = ( - 1, 3), B = (2, 1) oraz wiadomo, że C' = (5, - 3) jest obrazem punktu C w symetrii względem osi OX, a D' = ( - 2, 5) jest obrazem punktu D w symetrii względem osi OY. Oblicz obwód czworokąta ABCD i podaj równania jego osi symetrii.
71. Dane są punkty A = ( - 2, 1), B = (0, - 1), C = ( - 3, - 2), K = (2, 1), L = (4, - 1), M = (5, 2) są wierzchołkami trójkątów ABC i KLM. Wykaż, że te trójkąty są przystające.
72. Punkty A = (2, 4), B = ( - 2, 6), C = ( - 2, 2) są wierzchołkami równoległoboku ABCD. Oblicz współrzędne wierzchołka D i obwód tego równoległoboku.
73. Prostokąt A'B'C'D' jest obrazem prostokąta ABCD o wymiarach 4cm i 6cm w jednokładności o środku w punkcie A i skali k = - 0,5. Oblicz obwód i pole prostokąta A'B'C'D'.
74. Oblicz pole kwadratu, którego jednym z wierzchołków jest punkt A = (1, - 3) i którego przekątna zawiera się w prostej o równaniu y = 2x.
75. Dany jest trójkąt ABC o wierzchołkach A = (1, 0), B = (6, 0), C = (2,
). Jakie są miary kątów wewnętrznych tego trójkąta? Odpowiedź podaj w przybliżeniu z dokładnością do 1o.
76. Podstawą trójkąta równoramiennego ABC jest AB, gdzie A = (2, 1) i B = (5, 2). Ramię tego trójkąta zawiera się w prostej o równaniu 2x - y - 3 = 0. Oblicz pole trójkąta ABC.
77. Prosta x + y - 1 = 0 zawiera podstawę trójkąta równoramiennego. Jedno ramię trójkąta ma równanie x - 2y - 2 = 0. Znajdź równanie prostej zawierającej drugie ramię wiedząc, że przechodzi ona przez punkt P = ( - 2, 0).
78. W trójkącie ABC o wierzchołkach w punktach A = ( - 3, - 1), B = (1, 2), C = ( - 4, 7) punkt D jest środkiem boku BC. Oblicz pole trójkąta ABD.
79. Oblicz długość odcinka, którego końcami są punkty przecięcia paraboli y = x2 - 5x + 4 z prostą przechodzącą przez punkt P = (3, 7) i nachyloną do osi OX pod kątem 45o.
80. Oblicz współrzędne pozostałych wierzchołków równoległoboku ABCD gdzie B = ( - 1, 3),
C = (5, - 2) oraz M = (2, 0) jest punktem przecięcia przekątnych równoległoboku.
81. Sprawdź algebraicznie czy trójkąt o wierzchołkach A = (5, - 4), B = ( - 1, 2), C = ( - 4, - 1) jest trójkątem prostokątnym.
82. Dla jakich wartości parametrów a i b punkty A = (2, 3a - 2b) i A' = (a - b, 1 - 2a) są symetryczne względem:
Punktu (0, 0)
osi OX
83. W układzie współrzędnych zaznacz zbiór punktów, których pierwsza współrzędna jest większa od drugiej i suma obu współrzędnych jest mniejsza od 3.
84. Punkty A = (5, - 1), B = (1, 1) są symetryczne względem pewnej prostej. Wyznacz jej równanie.
85. Dla jakich wartości parametru k punkty A = (0, 0), B = (4, k) i C = (k, 9) leżą na jednej prostej?
86. Znajdź współrzędne punktu, który otrzymasz po obróceniu punktu P = (1, 0) wokół początku układu współrzędnych o kąt
.
87. Niech SA oznacz przekształcenie geometryczne, które jest symetrią względem punktu A = ( - 2, - 3) oraz niech X = (1, 2).
88. Wyznacz współrzędne punktu X' = SA(X).
89. Wyznacz współrzędne punktu A', który jest symetryczny do punktu A = (5, 8) względem prostej o równaniu 2x - y + 3 = 0.
90. Przekształcenie F jest takim przekształceniem płaszczyzny na płaszczyznę, w którym obrazem dowolnego punktu P = (x, y) jest punkt P' =
Oblicz współrzędne punktu A' = F(A), jeśli A = (3, - 3).
Podaj punkty stałe tego przekształcenia.
Znajdź równanie linii będącej obrazem prostej y = x + 5 w przekształceniu F.
XII Trygonometria
Oblicz wartość wyrażenia
.Oblicz (ctg251o
Oblicz stosując wzory redukcyjne
.Dla kąta rozwartego x zachodzi równość 2sin2x - 1 =
Oblicz cos tego kąta.Wiadomo, że x jest kątem ostrym oraz, że a = tgx + ctgx i b =
, Sprawdź, czy a2 = b2.Stosując wzory redukcyjne oblicz 2sin150o - 3cos120o + tg135o.
Wiadomo, że tgx + ctgx = 4. Oblicz
.Miary łukowe trzech kątów wynoszą
, 0,8
, 2.5. Zamień je na miary stopniowe i uporządkuj od największej do najmniejszej.Wiedząc, że tgx = - 3 oraz x
oblicz sinx.Wyznacz wartości funkcji trygonometrycznych kąta MON, jeśli M = (5, 0), O = (0, 0), N = ( - 4, 2).
Stosując wzory redukcyjne oblicz sin103o
.Oblicz wartość wyrażenia bez użycia tablic 3 -
Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego x wiedząc, że ctg =
.Wyznacz najmniejszą i największą wartość funkcji f określonej wzorem f(x) = 7 - 2cosx.
Wyznacz zbiór wartości funkcji f(x) = 3sinx - 3.
Narysuj wykres funkcji f(x) = 2sin
Wiedząc, że sinx cosx =
oblicz wartość wyrażenia sin4x + cos4x.Sprawdź następującą równość
.Uzasadnij tożsamość:
b)
c)
Wykaż, że dla x
prawdziwa jest równość tgx
.Wykaż tożsamość:
sin2x =
.
Od północy wskazówka obróciła się o kąt
. Która jest godzina?Pewnego dnia poziom wody (w metrach) na ławicy piaskowej u wejścia do portu wyrażał się wzorem y = 14 + 10sin
gdzie t oznacza liczbę godzin, jaka upłynęła od godziny 1200. Oblicz poziom wody w godzinach: 1400, 1500, 1600. O której godzinie tego dnia woda osiągnęła największy poziom?Sprawdź, że ctg10o - ctg20o =
.Rozwiąż równanie 1 + cos2x = cosx.
Uzasadnij, że sin2<2sin1.
Dla jakiej wartości parametru a istnieje rozwiązanie równania sinx = 2a - 3?
Ustal znak liczby ctg(cos0,3). Odpowiedź uzasadnij.
Dla jakich wartości parametru a
<0, 2
> równanie x2 -
x - cosa = 0 ma jeden pierwiastek podwójny?Wyznacz zbiór wartości funkcji określonej wzorem f(x) = sinx + cosx.
Sporządź wykres funkcji f w przedziale < - 2
> jeżeli f(x) = |sinx| - sinx.Narysuj wykres funkcji f(x) = -2sinxcosx dla x
i podaj jej miejsca zerowe oraz przedziały, w których funkcja przyjmuje wartości dodatnie.Rozwiąż równanie cos
.Zilustruj w układzie współrzędnych zbiór A =
Oblicz sin2x i cos2x, jeżeli sinx =
i 90o<x<180o.Wyznacz wszystkie liczby z przedziału (0,
) spełniające nierówność tg x > ctg x.Naszkicuj wykres funkcji f(x) = cos2x + |sinx|sinx dla x
<0,2
>.Naszkicuj wykres funkcji
b)
i omów własności.
49. Naszkicuj wykres
40. Rozwiąż równanie 2sin4x - 5sin2x + 2 = 0.
41. Określ zbiór wartości funkcji
.
42. Rozwiąż równanie 3sinx = 2cos2x.
43. Wyznacz największą ujemną liczbę spełniającą równanie
44. Rozwiąż równanie cos2x = cos x.
45. Uzasadnij tożsamość trygonometryczną
.
46. Dla jakich wartości parametru m równanie 3cosx - 2 = m ma rozwiązanie?
47. Wykonaj wykresy funkcji f(x) = x2 + 1 oraz g(x) = cos i rozwiąż równanie x2 + 1 = cos x.
48. Wiedząc, że tgx = 3, oblicz cos2x.
59. Rozwiąż nierówność cos<0,5, w przedziale <0,2
.
50. Wyznacz dziedzinę i zbiór wartości funkcji y =
.
51. Oblicz wartości pozostałych wartości funkcji trygonometrycznych kąta x, jeżeli sinx = 0,4 i x
52. Wyznacz okres zasadniczy funkcji g(x) = sin x + cos x.
53. Rozwiąż równanie cos3x = 0,5.
54. Wyznacz wszystkie liczby z przedziału
które spełniają nierówność tgx> - 1.
55. Mając dane tg
i tg
Oblicz tg
i tg
56. Wiedząc, że sinx + cos = a oblicz sin3x + cos3x.
57. Wyznacz okres funkcji f(x) = cos4x i rozwiąż równanie cos4x = -
dla x
58. Dla jakich wartości parametru m
R nie istnieje rozwiązanie równania sin3x =
69. Dla jakich x
60. Rozwiąż równanie 2cos
61. Rozwiąż równanie sin2x + cos = 0.
62. Rozwiąż nierówność 2sin2x + 1<0 dla x
63. Rozwiąż równanie ctg +
64. Dana jest funkcja
Wykazać, że jeżeli nie istnieje taka liczba całkowita k, że
to
Rozwiązać równanie f(x) = 3.
Wyznaczyć zbiór wartości funkcji.
65. Dana jest funkcja f(x) = sin2x.
Rozwiąż równanie f(2x) = f '(x).
Rozwiąż równanie 1 + f(x) + f2(x) + f3(x) + … = 2. którego lewa strona jest sumą nieskończonego szeregu geometrycznego.
Przy założeniu, że x
rozwiąż nierówność 3 -
66. Dane są funkcje f(x) = cos2x -
i g(x) = sinx.
Rozwiąż równanie 2f(x) = g(x) przy założeniu x
Wyznacz zbiór wartości parametru k, dla których równanie f(x) = g(x) + k nie ma rozwiązania.
Obliczyć wartość funkcji h(x) = 2f(x) + g(x) dla x =
67. Dana jest funkcja
Wyznacz dziedzinę funkcji.
Wykaż, że dla każdego x należącego do dziedziny f zachodzi równość
Rozwiąż równanie f(x) = 2 - cos2x.
XIII Funkcja wykładnicza
Rozwiąż nierówność
Rozwiąż nierówność
Rozwiąż graficznie nierówność
Rozwiąż równanie
Uzasadnij że
dla każdych x, y
.Wykonaj wykresy funkcji y = x2, y = x - 1 i rozwiąż nierówność
Dla jakich wartości argumentu x funkcja
ma wartości większe od 16?Wykonaj działania
Porównaj liczby
i zapisz w kolejności od największej do najmniejszej.Która z dwóch następujących liczb jest większa 2300 czy 3200?
Średnią geometryczną liczb dodatnich a1, a2,…,an gdzie n
{2, 3,…} nazywamy liczbę
. Oblicz średnią geometryczną liczb
3, 81, 90,
Wyznacz liczbę p spełniającą warunek
Wiadomo, że
. Oblicz w.Wyznacz wszystkie liczby całkowite p, które spełniają warunek
Uzasadnij, że liczba 8100 - 899 - 898 jest podzielna przez 55.
Sprawdź, że
.Rozwiąż równanie
Rozwiąż równanie
Wyznacz dziedzinę funkcji y =
Rozwiąż równanie f(0,25) + f(f(a4)) - 10f
gdzie f(x) =
i a
.Rozwiąż równanie
Przedstaw wyrażenie
Rozwiąż równanie 9x -
Rozwiąż nierówność
jeżeli
Wyznacz dziedzinę funkcji
Rozwiąż równanie (0,25)x + 4 =
.Wyznacz dziedzinę funkcji f, jeśli
Dla jakich x
R ciąg (16, 2x - 1, 4x - 3) jest ciągiem geometrycznym?Rozwiąż równanie 5x - 1 -
30. Oblicz
31. Rozwiąż równanie 32x + 2 - 10
32. Rozwiąż równanie
33. Naszkicuj wykres i podaj zbiór wartości funkcji f(x) = 2 - 3x.
34. Korzystając z własności funkcji wykładniczych określ znak liczby
35. Rozwiąż nierówność
36. Rozwiąż równanie 4x -
37. Oblicz
38. Rozwiąż nierówność
39. Wykonaj wykres funkcji
.
40. Rozwiąż nierówność
41. Wykonaj wykres funkcji f(x) = 2 - (0,5)x + 1 i omów jej własności.
42. Wyznacz najmniejszą liczbę całkowitą spełniającą nierówność
43. Oblicz wartość wyrażenia
44. Rozwiąż nierówność 9x
3x - 1 + 8.
45. Rozwiąż nierówność 0,5
46. Rozwiąż równanie
47. Wykres funkcji f(x) = ax + 2 - 1 przechodzi przez punkt (3, 31). Dla jakich x wartości funkcji są ujemne?
48. Rozwiąż równanie 2x + 4x = (2x + 1)2 - 2.
49. Rozwiąż nierówność
50. Rozwiąż nierówność
51. Rozwiąż nierówność 9x + 9
52. Rozwiąż nierówność 2|x - 1|<(0,5)3x - 2.
53. Wykonaj wykres funkcji
Czy funkcja jest różnowartościowa?
54. Wyznacz zbiór wartości funkcji f(x) =
dla x
< - 1, 2>.
55. Znajdź sumę wszystkich liczb całkowitych spełniających nierówność 2x +
56. Rozwiąż równanie 3x + 2 + 9x + 1 = 810.
57. Rozwiąż nierówność 4x + 2x + 1<8x.
58. Rozwiąż nierówność 2x + 2 - 5x + 1
.
59. Dla jakich wartości parametru m równanie ma dwa różne pierwiastki:
9x - 3x + 2 - 2m2 + 8 = 0.
60. Określ liczbę rozwiązań równania p(4x - 2x) = 1 - p w zależności od parametru p
61. Wyznacz zbiór wartości parametru m, dla których równanie m2x + (m + 3)2 - x = 4 ma co najmniej jedno rozwiązanie.
62. Rozwiąż równanie
63. Ile rozwiązań ma równanie 4x - 3x = 2
.
64. Wiedząc, że
Rozwiąż równanie f(2x) = - 3.
65. Rozwiąż równanie
66. Dla jakich wartości parametru m równanie (0,5)
67. Znajdź sumę wszystkich liczb całkowitych spełniających nierówność 2x +
68. Dana jest funkcja postaci
. Dla jakich wartości parametru a:
Nierówność f(x)<0 jest spełniona dla każdego x
Równość f(x) = 0 ma dokładnie jedno rozwiązanie.
Równanie f(x) = 0 ma dwa pierwiastki różnych znaków.
69. Dana jest funkcja
Dla jakich wartości parametru a:
a) Nierówność f(x)<0 jest spełniona dla każdego x
b) Równanie f(x) = 0 ma dokładnie jeden pierwiastek?
c) Równanie f(x) = 0 ma dwa pierwiastki różnych znaków.
70. Dane są funkcje
i g(x) = 42x - k.
a) Dla k = 2 rozwiąż nierówność f(x) =
b) Dla k =
rozwiąż nierówność f(x)
.
c) Wyznacz wszystkie wartości parametru k, dla których równanie f(x) = 21 - k ma dwa różne pierwiastki ujemne.
71. Dane są funkcje f(x) = 3x i g(x) = 6x - 2x + 1 + 8.
a) Rozwiąż nierówność [f(x)]2 - 6f(x) = 27.
b) Rozwiąż nierówność 4f(x)<g(x).
c) Sporządź wykres funkcji h(x) = |1 - f(x - 1)|. Korzystając z wykresu funkcji wyznacz liczbę pierwiastków równania h(x) = a w zależności od parametru a.
XIV Funkcja logarytmiczna
1. Dla jakich wartości parametru p funkcja y = log(2p - 3) x jest malejąca?
Rozwiąż układ równań
.Określ dziedzinę funkcji:
b)
.
Rozwiąż nierówność f(g(x))> - 2, jeżeli
, a g(x) = 5 + x2.Dla jakich wartości parametru k równanie logk + logx = 2log(x + 1) ma jeno rozwiązanie?
Rozwiąż równanie |x|log2(x + 3) = 2x.
Dla jakich wartości a zachodzi nierówność f(2a - 7)>2 jeżeli f(x) = - log2x.
Oblicz
Rozwiąż układ równań
.Wyznacz dziedzinę funkcji
Dla jakich wartości x
R ciąg (log2, log(2x - 1), log(2x + 3)) jest ciągiem arytmetycznym?Zbadaj dla jakiej wartości parametru a równanie x2 - 4x - loga = 0 ma rozwiązanie.
Określ znak liczby
.Sprawdź, że liczba a = log6216 - 5
jest wymierna.Dla jakich x funkcja f(x) = log(x - 1)4 przyjmuje wartość 2?
Wyznacz dziedzinę funkcji
Udowodnij, że jeżeli log34 = a to log227 =
.Oblicz log3(tg240o) - log
(tg240o).Rozwiąż równanie 2log5(x - 3) + log5(x + 3)2 = 0.
Dla jakich x funkcji f(x) = log0,5(x2 - 8) są dodatnie?
W układzie współrzędnych zaznacz zbiór punktów o współrzędnych (x, y), dla których sens ma wyrażenie log(log(y - x) - 1).
Dla jakich wartości parametru a równanie x2 + 2x - log9a2 = 0 nie ma rozwiązań?
Wykonaj wykres funkcji y = |log2|x||.
Rozwiąż nierówność log2sinx< - 1, x
Rozwiąż równanie log2x + logx = 0.
Rozwiąż nierówność log4(x - 1)<1 - log4(x + 2).
Rozwiąż równanie log5(log3(log2x)) = 0.
Rozwiąż nierówność
Wyznacz miejsca zerowe funkcji f(x) = log3x - log(2x + 3).
Niech log2 = a i log3 = b. Z użyciem liter a i b zapisz liczbę log
Oblicz
.Rozwiąż nierówność log3(2x - 4)<2.
Rozwiąż równanie log2(9 - 2x) = 3 - x.
Zbadaj istnienie pierwiastków równania x2 - 4x - log2a = 0 w zależności od parametru a.
Rozwiąż nierówność
Rozwiąż równanie:
b)
Rozwiąż nierówność:
b)
Oblicz sumę tych wszystkich liczb naturalnych n<100, które spełniają nierówność log2n + logn16>4.
XV Rachunek prawdopodobieństwa
1. Pewnego dnia Piotr miał gorączkę. Oto tabela obrazująca jego temperaturę w poszczególnych godzinach:
Godzina |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
Temp.[°C] |
38,4 |
38,6 |
39,0 |
38,9 |
38,5 |
38,5 |
38,4 |
38,0 |
Sporządź wykres tej zależności i połącz punkty odcinkami. Na podstawie otrzymanej linii odczytaj, jaką temperaturę miał Piotr o godzinie 15.00. O której godzinie Piotr miał temperaturę 38,4°C?
2. Badania wykazały, że co piąty Polak kupuje na kredyt z przeznaczeniem na: samochód - 28% kredytobiorców, dom i mieszkanie - 24%, meble - 20%, podróże i wakacje - 10% a pozostali kredytobiorcy na zakup sprzętu AGD. Narysuj wykres słupkowy ilustrujący ile procent kredytobiorców przeznacza kredyt na poszczególne cele. Jaki procent wszystkich Polaków bierze kredyt na wakacje i podróże?
3. Ostatnie cyfry kwadratów kolejnych liczb naturalnych tworzą ciąg 1, 4, 9, 6, 5,... Wykonaj histogram słupkowy obrazujący częstość występowania danej cyfry wśród stu początkowych wyrazów tego ciągu.
Prawdopodobieństwo, że w danym dniu świeci słońce w miejscowości M wynosi 5:6. Przyjeżdżamy na 14 - dniowy urlop do M. Jakie jest prawdopodobieństwo, że słońce będziemy mieli dokładnie przez 10 dni?
Mamy dwie urny z białymi i czarnymi kulami. W pierwszej urnie jest 5 kul białych i 3 czarne, a w drugiej jest 6 kul białych i 2 czarne. Z losowo wybranej urny losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na ty, że będzie to kuła czarna.
Trzykrotnie rzucamy kostką do gry. Oblicz prawdopodobieństwo wyrzucenia sumy oczek większej od 10, jeśli wiadomo, że suma oczek w dwóch pierwszych rzutach jest równa 5.
Rzucamy jeden raz kostką do gry. Niech A - zdarzenie polegające na wyrzuceniu nieparzystej liczby oczek. B - zdarzenie polegające na wyrzuceniu liczby oczek podzielnej przez 3. Czy zdarzenia A i B są niezależne?
Z urny zawierającej dziewięć jednakowych kul ponumerowanych od 1 do 9 losujemy kolejno trzy kule bez zwracania. Oblicz prawdopodobieństwo tego, że numery wszystkich wylosowanych kul będą parzyste.
W rajdzie pieszym uczestniczy grupa młodzieży składająca się z pięciu harcerek i czterech harcerzy. Maszerują w szyku zwanym „gęsiego". Ile istnieje różnych sposobów ustawienia się, jeżeli harcerze nie mogą sąsiadować z harcerzami a harcerki z harcerkami?
Ile istnieje różnych liczb 4-cyfrowych o nie powtarzających się cyfrach, zaczynających się od cyfry 1, 3 lub 5?
W Masie liczącej 20 chłopców należ wybrać dwie 6-osobowe drużyny do turnieju siatkówki: drużyna pierwsza zagra w I lidze, a druga w II lidze. Ile istnieje sposobów sformowania wspomnianych drużyn, jeżeli każdy uczeń może być zawodnikiem tylko jednej drużyny?
Na pewnej uczelni obowiązuje następująca skala ocen: 2, 3, 4, 5. Egzamin nie jest zdany, gdy otrzymana z niego ocena jest równa 2. Czterech studentów tej uczelni stawiło się na egzamin. Na ile sposobów mogą im być wystawione oceny, jeżeli wszyscy zdali egzamin?
Rozwiąż równanie
gdzie
oznacza liczbę wszystkich k-elementowych kombinacji zbioru n-elementowego.Ile różnych liczb 5-cyfrowych można utworzyć z cyfr: 0, 1, 2, 3, 4 takich, aby żadne cyfry w liczbie się nie powtarzały?
Rzucamy czterokrotnie monetą. Wypisz zdarzenia elementarne, które sprzyjają zdarzeniu A'
B gdy A - zdarzenie polegające na wyrzuceniu co najmniej dwóch reszek, B - zdarzenie polegające na wyrzuceniu nieparzystej liczby orłów.Strzelec trafia w tarczę z prawdopodobieństwem 0,9. Na każde 10 strzałów trafiających w tarczę 2 trafiają w dziesiątkę. Oblicz prawdopodobieństwo, że strzelając jeden raz strzelec trafi w dziesiątkę.
Z pięciu prętów o długościach 1, 2, 3, 4, 5 wybieramy losowo trzy. Oblicz prawdopodobieństwo tego, że można z nich zbudować trójkąt prostokątny.
Z talii 52 kart pięć razy losujemy jedną kartę i po każdym losowaniu zwracamy ją do talii i tasujemy. Jakie jest prawdopodobieństwo tego, że uda nam się w ten sposób trzykrotnie wylosować króla?
Wykonujemy serię 12 rzutów dwiema kostkami. Jakie jest prawdopodobieństwo tego, że co najmniej raz suma oczek na obu kostkach będzie większa od 10?
Co jest bardziej prawdopodobne: w rzucie dwiema kostkami wyrzucenie sumy oczek nie mniejszej niż li czy w rzucie czterema monetami wyrzucenie co najmniej trzech orłów?
Z urny zawierającej cztery kule: 2 białe i 2 czarne losujemy cztery razy bez zwracania po jednej kuli. Jakie jest prawdopodobieństwo tego, że białe kule będą wylosowane przed czarnymi?
Dwaj strzelcy równocześnie strzelają jeden raz do tarczy. Jeden z nich trafia do celu 7 razy na 10 strzałów, drugi 8 na 10 strzałów. Jakie jest prawdopodobieństwo tego, że przynajmniej jeden z nich trafi do tarczy?
29. Rzucamy trzykrotnie kostką. Jakie jest prawdopodobieństwo wyrzucenia sumy oczek większej niż 14, jeśli w pierwszych dwóch rzutach suma ta wynosiła 10?
XVI Analiza matematyczna
Czy zbiór
jest sąsiedztwem punktu x0.Oblicz granicę
Oblicz granicę funkcji
.W zależności od parametru k oblicz granicę funkcji
.Dla jakiej wartości parametru k zachodzi równość
Oblicz granicę
Oblicz
Oblicz granicę funkcji
Oblicz granicę funkcji h(x) =
Oblicz granicę funkcji f w punkcie x0 = 1, jeśli
.Oblicz f '(1) dla funkcji określonej wzorem
Dana jest funkcja f określona wzorem
Oblicz f `( - 1).Wykaż, że pochodna funkcji f(x) = 2tgx + x2sinx jest funkcją parzystą.
Dana jest funkcja określona wzorem f(x) = x2 - 2x - 2. Rozwiąż nierówność
2 + f(1 - x)>f `(2x) + f `(x).
Korzystając z definicji pochodnej funkcji w punkcie oblicz f `(2) jeśli f(x) = x2 + 1.
Dla jakiej wartości parametru m liczba x = 1 jest miejscem zerowym pochodnej funkcji f(x) = x3 - 2mx2 + 2?
Uzasadnij istnienie rozwiązania równania x3 + 3x + 2 = 0.
Oblicz pochodną funkcji
Oblicz pochodną funkcji f w punkcie x = 2, jeśli
oraz g(2) = h(2) = 3 i
g'(2) = 8 = - 2h'(2)
Wyznacz miejsce zerowe pochodnej funkcji P(r) = 2
Wyznacz pochodną funkcji
Na podstawie definicji oblicz pochodną funkcji f(x) = x2 + x w punkcie x0.
Niech f(x) =
. Rozwiąż nierówność f(x)<f `(x).Wyznacz pochodną funkcji g(x) =
Wyznacz pochodną funkcji y =
.Znajdź pochodną funkcji f(x) = xsinx.
Znajdź równanie stycznej do krzywej y = x + sinx w punkcie x = 0.
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji f(x) = cos22x cos w punkcie M = (x0, f(x0)), jeśli x0 =
Do wykresu funkcji f(x) = 2x2 + 1 poprowadzono styczną w punkcie A = ( - 1, 3). W jakim punkcie styczna ta przecina oś OY?
Zbadaj, czy istnieje styczna do krzywej o równaniu y =
i równoległa do prostej o równaniu
y = - x?
Sprawdź, czy styczna do wykresu funkcji określonej wzorem f(x) = 2x2 + x - 1 w punkcie A = (1, 2) jest prostopadła do prostej o równaniu x + 4y + 8 = 0.
Oblicz tangens kąta przecięcia się wykresów funkcji f i g w punkcie, którego odcięta jest liczbą parzystą, jeśli f(x) = x2, a g(x) = 3x - 2.
33. Współczynnik kierunkowy stycznej do wykresu funkcji f(x) = x3 + 2x2 - x - 2 wynosi a = - 2. Wyznacz punkty styczności stycznej z wykresem funkcji f.
34. Wykaż, że krzywe o równaniach y = x - x2 i y = x2 - x przecinają się pod kątem prostym.
35. Znajdź tangens kąta między krzywymi o równaniach y = x2 i y =
36. Uzasadnij, że prosta y = 2x - 1 jest styczna do paraboli y = x2.
37. Wyznacz równanie stycznej do hiperboli y =
w punkcie M = (2, 3).
38. Wyznacz współczynnik kierunkowy stycznej do krzywej y = x2 w punkcie A = (1, 1).
39. Wyznacz parametry a i b wiedząc, że funkcja y = x3 + ax + b w punkcie x = 3 osiąga ekstremum równe 1.
40. Wyznacz wartości parametru k wiedząc, że w punkcie x = 1 funkcja f(x) = x3 + 2x2 osiąga ekstremum. Czy jest to maksimum czy minimum?
41. Wyznacz asymptoty wykresu funkcji
42. Zbadaj ekstrema funkcji f(x) = (x2 - 2x + 2) - 1.
43. Wyznacz najmniejszą i największą wartość funkcji f(x) = cosx - sinx.
44. Wyznacz ekstrema funkcji
45. Wyznacz najmniejszą i największą wartość funkcji f(x) = cos - sinx.
46. Dla jakich wartości m funkcja określana wzorem
jest funkcją rosnącą w zbiorze liczb rzeczywistych?
47. Funkcja f określana wzorem
posiada ekstremum dla x = 1. Zbadaj czy jest to maksimum czy minimum?
48. Czy istnieje asymptota pozioma wykresu funkcji
. Uzasadnij odpowiedź.
49. Wyznacz współczynnik funkcji postaci f(x) = 12x3 + bx2 + cx + d tak, aby osiągnęła ona w punktach x = 1 i x =
ekstrema i aby liczba 1 była jej miejscem zerowym.
50. Zbadaj monotoniczność funkcji określonej wzorem f(x) = 5x + cos4x.
51. Czy Prosta o równaniu x = 6 jest asymptotą pionową wykresu funkcji określonej wzorem
52. Uzasadnij dlaczego funkcja f(x) = 3x + 2sinx nie posiada ekstremów.
53. Wyznacz równania asymptot wykresu funkcji określonej wzorem
54. Ustal najmniejszą i największą wartość funkcji
w przedziale < - 0,5; 0,5>.
55. Wyznacz przedziały monotoniczności funkcji f(x) = 2x3 - 9x2 - 60x + 6.
56. Określ przedziały monotoniczności funkcji y = 2x3 - 3x2 - 12x + 1.
57. Wyznacz najmniejszą i największą wartość funkcji
w przedziale <0, 3>.
58. Podaj ekstrema funkcji
.
59. Wyznacz asymptoty wykresu funkcji
60. Wyznacz przedziały monotoniczności funkcji
.
61. Z dużego arkusza blachy należy wyciąć prostokąt o polu równym 2025cm2. Jak należy dobrać wymiary tego prostokąta, aby jego obwód był najmniejszy?
62. Wyznacz wymiary prostokąta o obwodzie 20cm tak, aby jego pole było największe?
63. Ze wszystkich prostokątów o danym polu S wybierz ten, który ma najmniejszy obwód.
64. Jaki prostokąt o obwodzie 36cm ma najkrótszą przekątną?
65. Suma długości boku trójkąta i wysokości opuszczonej na ten bok wynosi 100cm. Ile centymetrów powinien mieć bok, a ile wysokość, aby pole trójkąta było największe?
66. Uzupełnij wzór funkcji
tak, by jej dziedziną był zbiór liczb rzeczywistych i żeby była ciągła w każdym punkcie dziedziny.
67. Narysuj wykres pewnej funkcji f, która spełnia następujące warunki:
Dziedziną jest zbiór R/{ - 3, 1}.
jest ciągła w swojej dziedzinie.
,
,
68. Zbadaj ciągłość funkcji określonej wzorem
69. Dlaczego funkcja f określona wzorem
nie jest ciągłą w punkcie x0 = 0?
70. Zbadaj ciągłość funkcji
71. Zbadaj ciągłość funkcji określonej wzorem
72. Wykonaj wykres funkcji
i zbadaj jej ciągłość.
73. Dla jakiej wartości parametru m funkcja
74. Dla jakich wartości b funkcja f będzie ciągła w punkcie x0 = 1 jeżeli
dla x
75. Wykonaj wykres funkcji
dla tej wartości parametru m, dla której funkcja f jest ciągłą.
XVII Stereometria
Oblicz pole powierzchni graniastosłupa prostego, którego przekątna ściany bocznej ma długość b, zaś podstawą jest trójkąt równoboczny o boku długości a.
Na sześcianie o krawędzi o długości a opisano kulę w ten sposób, że wierzchołki sześcianu należą do powierzchni kuli. Oblicz objętość kuli.
Wśród prostopadłościanów o podstawie kwadratowej i danej objętości V znajdź prostopadłościan, dla którego suma długości wszystkich krawędzi jest najmniejsza.
Przekątna prostopadłościanu ma długość 8, a miara kąta jaki tworzy ona ze ścianą boczną wynosi 30°. Oblicz objętość prostopadłościanu, jeśli jego wysokość ma długość 2
Z prostokątnego arkusza tektury wykonano otwarte pudełko wycinając w czterech rogach kwadraty o boku 4cm i zaginając brzegi. Objętość tego pudełka równa się 1536cm2. Jakie wymiary miał ten arkusz , jeśli wiadomo, że jego długość była dwa razy większa niż szerokość.
Wymiary prostopadłościanu są trzema kolejnymi liczbami naturalnymi. Jakie są długości krawędzi, jeśli prostopadłościan ma objętość mniejszą niż 120?
Jeżeli każdą krawędź sześcianu powiększymy o 3cm, to objętość sześcianu powiększy się o 819cm2. Ile wynosi długość krawędzi sześcianu?
W graniastosłup prawidłowy trójkątny wpisano walec w ten sposób, że podstawy walca są wpisane w podstawy graniastosłupa. Oblicz pole powierzchni bocznej tego walca jeżeli każda krawędź graniastosłupa wynosi a.
Oblicz pole powierzchni całkowitej S sześcianu, którego przekątna ma długość 8
.W graniastosłupie prawidłowym czworokątnym przekątna o długości 4cm jest nachylona do płaszczyzny podstawy pod kątem 30°. Oblicz objętość graniastosłupa.
Dany jest sześcian o boku długości a. Wyznacz tangens kąta między przekątnymi tego sześcianu.
Objętość prostopadłościanu wynosi 216. Długości krawędzi są wyrazami ciągu geometrycznego i ich suma wynosi 21. Znajdź pole powierzchni całkowitej tego prostopadłościanu.
W sześcianie o boku a ścięto każde naroże płaszczyzną przechodzącą przez środki trzech krawędzi zbiegających się w jednym narożu. Oblicz objętość powstałej w ten sposób bryły.
Oblicz stosunek objętości sześcianu do objętości kuli opisanej na tym sześcianie.
Przekrój ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i wierzchołek ostrosłupa jest trójkątem równobocznym o polu S. Oblicz objętość ostrosłupa.
Wysokość ściany bocznej prawidłowego ostrosłupa czworokątnego ma długość a i tworzy z płaszczyzną podstawy kąt o mierze a. Oblicz objętość ostrosłupa.
Oblicz pole ostrosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość a i tworzy z krawędzią boczną kąt o mierze
.W ostrosłupie prawidłowym sześciokątnym krawędź podstawy ma długość 4, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma 30°. Oblicz objętość tego ostrosłupa.
Czworościan foremny ma krawędź długości 2. Oblicz pole powierzchni tego przekroju czworościanu, który zawiera jego pamięć i wysokość.
Wysokość ostrosłupa prawidłowego trójkątnego równa się połowie krawędzi podstawy. Oblicz kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.
Oblicz objętość ostrosłupa czworokątnego prawidłowego jeżeli krawędź boczna o długości 5cm jest nachylona do płaszczyzny podstawy pod kątem 60°.
Oblicz pole przekroju czworościanu foremnego o krawędzi a jedną z płaszczyzn symetrii.
Objętość czworościanu foremnego jest równa 18
. Oblicz objętość kuli wpisanej w ten czworościan.
24. Oblicz objętość prawidłowego ostrosłupa czworokątnego, wiedząc że przekrój ostrosłupa płaszczyzną przechodzącą przez przekątną podstawy i wierzchołek ostrosłupa jest trójkątem równobocznym o polu S.
Krawędź boczna ostrosłupa trójkątnego prawidłowego ma długość 6cm i tworzy z płaszczyzną podstawy kąt o mierze 30°. Oblicz objętość ostrosłupa.
O ile trzeba zwiększyć długość promienia kuli, aby jej objętość zwiększyła się dwukrotnie?
Podaj określenie kąta między prostą a płaszczyzną. Powierzchnia boczna stożka po rozcięciu wzdłuż tworzącej jest półkolem. Oblicz kąt nachylenia tworzącej stożka do płaszczyzny podstawy.
Oblicz objętość stożka o wysokości H, wiedząc że jego przekrój osiowy jest:
a. trójkątem równobocznym
b. trójkątem prostokątnym
Tworząca stożka ma długość 1. Dla jakiej długości wysokości stożek ten ma maksymalną objętość?
Przekrój osiowy stożka jest trójkątem równobocznym o boku a. Oblicz pole powierzchni całkowitej stożka.
W kulę o promieniu R wpisano walec. Jaką wysokość powinien mieć ten walec, by jego objętość była maksymalna?
Przekrój osiowy stożka jest trójkątem równoramiennym prostokątnym, którego przyprostokątna ma długość a. Oblicz pole powierzchni stożka.
Ile trzeba zwiększyć długość r promienia kuli, aby jej objętość zwiększyła się dwukrotnie?
Kulę o promieniu r przetopiono na walec, którego przekrój osiowy jest kwadratem. Jaka jest wysokość walca?
Wysokość walca jest o 3cm większa od średnicy jego podstawy. Pole powierzchni całkowitej walca wynosi 120
cm2. Oblicz wymiary walca.
Rozwinięta płaszczyzna boczna stożka jest ćwiartką koła. Oblicz cosinus kąta rozwarcia stożka.
Podaj definicję poszczególnych brył obrotowych. Oblicz objętość bryły powstałej przez obrót trapezu prostokątnego o podstawach a = 3cm i b = 4cm oraz dłuższej przekątnej d = 6cm wokół krótszej podstawy.
Oblicz maksymalną objętość walca wpisanego w stożek o promieniu podstawy r = 2cm i wysokości h = 6cm.
Promień podstawy stożka ma długość r. Przekrój osiowy stożka jest trójkątem prostokątnym. Wyznacz pole tego przekroju.
W stożek, którego przekrój osiowy jest trójkątem równobocznym wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.
Oblicz objętość bryły powstałej przez obrót trapezu równoramiennego o podstawach a, b (a>b) i wysokości c dookoła krótszej podstawy.
Przekątna prostokąta o długości d = 6 tworzy z jednym z boków kąt o mierze 60°. Oblicz pole powierzchni całkowitej bryły powstałej po obrocie tego prostokąta dookoła krótszego boku.
Trójkąt o ramionach 6cm i kącie rozwartym 120° obraca się dookoła podstawy. Oblicz pole powierzchni powstałej bryły.
Przekrój osiowy stożka wpisanego w kulę o promieniu r = 5cm jest trójkątem równoramiennym prostokątnym. Oblicz pole powierzchni bocznej stożka.
Wiedząc, że objętość stożka jest równa V i tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem a , oblicz pole powierzchni bocznej stożka.
Walec ma pole powierzchni całkowitej 24cmk2, a jego przekrój osiowy ma pole 8cm2. Oblicz długość podstawy i długość wysokości walca.
Dany jest czworościan foremny ABCD, którego krawędź ma długość a. Punkt K jest środkiem wysokości DD1 tego czworościanu.
a. Wyznacz miarę kata AKB.
b. Wyznacz stosunek długości promienia kuli wpisanej w czworościan do długości wysokości tego czworościanu.
c. Płaszczyzna równoległa do podstawy czworościanu i przechodząca przez punkt K dzieli go na dwie bryły. Oblicz stosunek objętości otrzymanych brył.
48. W stożku jest dana miara kąta rozwarcia a oraz pole przekroju osiowego P.
a. Oblicz objętość kuli wpisanej w ten stożek jeśli
= 60° a P = 12
.
b. Oblicz objętość i pole powierzchni bocznej stożka
c. Wiadomo, że
= 120°. Stożek przecięto płaszczyzną równoległą do płaszczyzny podstawy. Oblicz objętość bryły od wierzchołka do tej płaszczyzny wiedząc, że pole otrzymanego przekroju wynosi 75
.
49. Dany jest ostrosłup prawidłowy czworokątny.
a. Oblicz promień kuli wpisanej objętość ten ostrosłup jeżeli wiadomo, że pole powierzchni jednej ściany bocznej jest równe S, zaś kat nachylenia tej ściany do płaszczyzny podstawy ma miarę
.
b. Oblicz objętość tego ostrosłupa mając dane: pole P przekroju osiowego tego ostrosłupa, przekątną podstawy oraz miarę kąta nachylenia krawędzi bocznej do płaszczyzny podstawy równą
.
c. Oblicz miarę kąta nachylenia płaszczyzny ściany bocznej do płaszczyzny podstawy jeśli kąt dwuścienny między sąsiednimi ścianami ma miarę 120o.
50. Dany jest graniastosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość a.
a. Wiedząc, że przekątna ściany bocznej tworzy z dragą ścianą boczną kąt o mierze a. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
b. Płaszczyzna przechodząca przez krawędź podstawy graniastosłupa podzieliła go na dwie bryły, których stosunek objętości wynosi 1/3. Oblicz miarę kąta nachylenia tej płaszczyzny do płaszczyzny podstaw, jeśli wiadomo, że wysokość graniastosłupa jest dwa razy dłuższa od krawędzi podstawy.
c. Oblicz pole powierzchni kuli opisanej na tym graniastosłupie, wiedząc, że jego pole powierzchni bocznej jest cztery razy większe od pola powierzchni podstawy.
Akademia Górniczo - Hutnicza im. Stanisława Staszica w Krakowie 2000
Czas rozwiązywania: 150min. Każde zadanie warte jest 15punktów.
Kandydaci rozwiązują 4 wybrane zadania.
ZADANIE 1
Oblicz sumę nieskończonego ciągu geometrycznego a + aq + aq2 + ..., w którym
natomiast q jest pierwiastkiem równania:
ZADANIE 2
Grupę k obiektów kosmicznych obserwuje m stacji radiolokacyjnych. Każdy obiekt jest niezależnie od innych wykrywany przez stację radiolokacyjną z prawdopodobieństwem p. Oblicz prawdopodobieństwa następujących zdarzeń:
A - co najmniej jeden obiekt zostanie wykryty,
B - nie każda stacja wykryje wszystkie obiekty,
C - losowo wybrana stacja wykryje n obiektów (n mniejsze lub równe k)
D - wszystkie obiekty zostaną wykryte.
ZADANIE 3
Wyznacz zbiór tych wartości parametru k, dla których dziedziną funkcji
jest zbiór:
a) wszystkich liczb rzeczywistych,
b) wszystkich liczb rzeczywistych dodatnich.
ZADANIE 4
Spośród trójkątów o wierzchołkach A(m - 2,m - 2), B(m + 6,1), C(9,m + 4) wybierz ten, w którym kosinus kąta wewnętrznego przy wierzchołku A wynosi 0,8, a długość okręgu na nim opisanego jest równa 10p. Napisz równanie okręgu wpisanego w wybrany trójkąt.
ZADANIE 5
Wyznacz promień najmniejszej kuli, w której mieszczą się cztery kule o promieniu r ułożone w ten sposób, że każda z nich jest styczna do trzech pozostałych.
Zadanie 01
Zaznacz w układzie współrzędnych zbiory : A = { (x , y) ; x∈R i y∈R i x + y ≤ 1 } oraz
B = { (x , y) ; x∈R i y∈R i 4x2 + 4y2 - 4x ≤ 15 } Zaznacz osobno zbiór B\A
(*) Niech m∈N. Oznaczmy zbiory :
Am = { (x , y) ; x∈R i y∈R i |x| + |y| ≤ m } oraz
Bm = { (x , y) ; x∈R i y∈R i 4x2 + 4y2 - 4x ≤ 4m + 1 }
Dla jakich wartości m zachodzi zawieranie Am ⊂ Bm
Zadanie 02
Dla jakich wartości parametru k istnieją dwa różne pierwiastki rzeczywiste równania:
x2 - ( k + 7 )x + k + 6 = 0 spełniające nierówność (x1 + x2)2 ≥ 6x1x2 - 2
Zadanie 03
Zbadaj liczbę rozwiązań układu równań :
w zależności od parametru m. Dla jakich całkowitych wartości parametru m rozwiązaniem tego układu jest para liczb dodatnich ?
Zadanie 04
Naszkicuj wykres funkcji
, następnie na podstawie wykresu podaj liczbę rozwiązań równania
, w zależności od parametru m
Zadanie 05
Rozwiąż układ równań :
Dla jakich wartości parametru m punkt przecięcia się prostych danych równaniami układu należy do prostej x + 2y - 3 = 0.
Zadanie 06
Dany jest wierzchołek kwadratu A(1; - 3) i prosta y = 2x, w której zawiera się przekątna BD. Wyznacz współrzędne pozostałych wierzchołków kwadratu i oblicz jego pole.
Zadanie 07
Dany jest okrąg o równaniu x2 + y2 = 8 i prosta y = - x + 8. Napisz równanie okręgu o najmniejszym promieniu stycznego jednocześnie do danego okręgu i danej prostej.
Zadanie 08
Dany jest ciąg o wyrazie ogólnym:
, oblicz granicę tego ciągu, zbadaj jego monotoniczność i podaj, które wyrazy ciągu są mniejsze od
.
Zadanie 09
W ostrosłupie trójkątnym prawidłowym krawędź podstawy ma długość a, zaś kąt nachylenia krawędzi bocznej do podstawy ma miarę α . Wyznacz objętość ostrosłupa. Oblicz ją dla a = 6 i α = 450.
Zadanie 10
Dwoma wierzchołkami trójkąta ABC są punkty, w których prosta x + y = 4 przecina parabolę y = x2 - 6x + 8, zaś trzecim jest wierzchołek tej paraboli. Wyznacz wierzchołki trójkąta, zbadaj czy jest on prostokątny i oblicz jego pole.
Zadanie 11
Pierwiastkami wielomianu W(x) = x3 + ax2 + bx + 4 są liczby x1 i x2, gdzie x1 to prawdopodobieństwo wyrzucenia takich samych wyników przy dwukrotnym rzucie monetą, zaś x2 to rozwiązanie równania 2x - 2 + 2x + 1 - 2x = 20. Wyznacz współczynniki a, b i rozwiąż nierówność W(x) > 0.
Zadanie 12
W ciągu arytmetycznym a8 = 23, S8 = 100. Ile wyrazów tego ciągu daje w sumie 392 ?
Zadanie 13
W okrąg o równaniu x2 + y2 = 25 wpisano prostokąt, w ten sposób, że dwa jego wierzchołki należą do prostej o równaniu 2x - y = 5. Oblicz pole tego prostokąta.
Zadanie 14
Podstawą ostrosłupa jest kwadrat o boku a = 2
. Krawędź boczna tworzy z podstawą kąt
. Oblicz objętość ostrosłupa.
Zadanie 15
Rozwiąż równanie : 2 + 5 + 8... + x = 187 wiedząc, że lewa strona jest sumą ciągu arytmetycznego.
Zadanie 16
Oblicz pole trójkąta wyznaczonego przez punkty A(1; - 1); B(4;5); C(1;4).
Zadanie 17
Podaj wszystkie liczby naturalne należące do przedziału
gdzie a jest wartością wyrażenia :
, natomiast b jest pierwiastkiem równania :
log4{log3[log2(x - 2)]} = 0
Zadanie 18
Dla jakiej wartości parametru m równanie mx2 + (2m - 4)x + m - 3 = 0 ma dwa pierwiastki spełniające warunek :
Zadanie 19
Dane są zbiory :
A = { x ; x∈R i x3 - 3x2 - 4x + 12>0 } B = { x ; x∈R i
}
C = { x ; x∈R i |x + 1|<2 }. Wyznacz : (A∪B)∩C
Zadanie 20
Dla jakich wartości parametru m równanie mx4 + (3 - m)x2 + m = 0 ma 4 różne pierwiastki rzeczywiste ?
Zadanie 21
Dane są punkty A(8; - 1) ; B(10;11) oraz prosta l o równaniu x - y + 3 = 0
Wyznacz punkt C leżący na prostej l , równoodległy od A i B
Wykaż, że trójkąt ABC jest prostokątny
Oblicze pole trójkąta ABC
Napisz równanie okręgu opisanego na tym trójkącie.
Zadanie 22
Długości krawędzi kartonika na sok owocowy tworzą ciąg geometryczny. Oblicz długości tych krawędzi wiedząc, że pojemność kartonika to jeden litr, a na jego wykonanie potrzeba 700 cm2 kartonu.
Zadanie 23
Wyznacz argument x, dla którego wyrażenia log2(x - 6), log2(2x), log2(x2 + 8x), są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma ilu wyrazów tego ciągu jest równa 330?
Zadanie 24
Z liczb 1,2,3,4,5 losujemy bez zwracania kolejno dwie liczby. Oblicz prawdopodobieństwo zdarzeń:
A - suma wylosowanych liczb jest większa od 7;
B - za pierwszym razem wylosowano liczbę nieparzystą;
A/B - suma wylosowanych liczb jest większa od 7 pod warunkiem, że pierwsza liczba jest nieparzysta. Zbadaj niezależność zdarzeń A i B.
Zadanie 25
Podstawą graniastosłupa prostego jest trójkąt ABC, w którym |AC| = 2 , kąt CAB = 600 , kąt ABC = 450 . Przekątna największej ściany bocznej tworzy z płaszczyzną podstawy kąt 600. Oblicz objętość i pole powierzchni bocznej tego graniastosłupa.
Zadanie 26
W ostrosłupie prawidłowym czworokątnym pole powierzchni jednej ściany bocznej równa się S. Kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 2α . Oblicz objętość tego ostrosłupa.
Zadanie 27
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna o długości d tworzy z wysokością kąt α . Wyprowadź wzór na objętość walca. Oblicz ją dla
i α = 600 .
Zadanie 28
Funkcja
osiąga ekstremum dla x = - 1. Wyznacz współczynnik m , przy wyznaczonym m zbadaj przebieg zmienności funkcji i naszkicuj jej wykres.
Zadanie 29
Zbadaj przebieg zmienności funkcji :
Zadanie 30
Zbadaj przebieg zmienności funkcji :
Na podstawie wykresu określ liczbę rozwiązań równania
w zależności od parametru k.
Zadanie 31
Z kawałka drutu o dł. 72 cm zrobiono szkielet prostopadłościanu o podstawie kwadratowej. Wyznacz objętość prostopadłościanu jako funkcję krawędzi podstawy x. Dla jakiego x objętość prostopadłościanu jest maksymalna.
Zadanie 32
Jakie powinny być długości przyprostokątnych w trójkącie prostokątnym, którego przeciwprostokątna ma długość
, aby stożek otrzymany w wyniku obrotu dookoła jednej przyprostokątnej miał maksymalną objętość.
Zadanie 33
Pierwszy wyraz ciągu arytmetycznego jest równy mniejszemu, a piąty większemu pierwiastkowi równania log(x + 6) - 2 = 0,5log(2x - 3) - log25. Wyznacz ten ciąg. Ile wyrazów tego ciągu daje w sumie 150 ?
Zadanie 34
Rozwiąż równanie: 1 + 5 + 9 + ... + x = 153.
Zadanie 35
Dla jakich wartości parametru m odcięta wierzchołka paraboli y = x2 -2(m - 1)x + m3 - 3 należy do przedziału
, gdzie a jest granicą ciągu
, zaś b jest rozwiązaniem równania
Zadanie 36
Suma długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka wynosi 18. Długość jednej z nich jest 2 razy większa niż drugiej. Wyznacz długości krawędzi prostopadłościanu tak, by miał on maksymalną objętość.
Zadanie 37
Właściciel sklepu kupuje aparaty fotograficzne u producenta po 100 zł. za sztukę i sprzedaje 40 sztuk miesięcznie po 160 zł. Właściciel oszacował, że każda kolejna obniżka ceny aparatu o 1 zł. zwiększa sprzedaż o jedną sztukę. Jak powinien sprzedawca ustalić cenę aparatu, aby jego zysk był największy ?
Zadanie 38
Suma dziewięciu pierwszych wyrazów ciągu arytmetycznego wynosi 18, a suma siedmiu pierwszych wyrazów tego ciągu jest równa 0. Wyrazy a7, a8, a9 są miarami długości boków trójkąta . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim.
Zadanie 39
W graniastosłupie prawidłowym, trójkątnym pole powierzchni bocznej równa się sumie pól obu podstaw. Oblicz cosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.
Zadanie 40
Dana jest funkcja f(x) = x3 + kx2 + m. Liczba -2 jest miejscem zerowym funkcji i jej pochodnej. Naszkicuj funkcję g(x) = |f(x)|
Zadanie 41
Dane są zbiory:
oraz
Wyznacz zbiór
Zadanie 42
Rozwiąż równanie cos2x + sinx = p2 + 4q + 3 wiedząc, że p jest większym pierwiastkiem równania
, zaś
.
Zadanie 43
Dwusieczna kąta prostego w trójkącie prostokątnym o przeciwprostokątnej dł. 35cm dzieli tą przeciwprostokątną w stosunku 3:4. Oblicz stosunek pola koła wpisanego w ten trójkąt do pola koła opisanego na nim.
Zadanie 44
Dana jest prosta k: 2x - y + 1 = 0 i okrąg x2 + y2 - 4x - 1 = 0. Wykaż, że prosta jest styczna do okręgu. Napisz równanie okręgu symetrycznego do danego względem prostej k.
Zadanie 45
Mamy trzy identyczne pudełka i w każdym 10 losów. W pierwszym są trzy losy pełne, w drugim cztery, a w trzecim siedem. Możemy wylosować trzy losy jednym ze sposobów:
losujemy jedno pudełko i z niego trzy losy,
z każdego pudełka losujemy po jednym losie,
zsypujemy wszystkie losy do jednego pudełka i losujemy trzy losy.
Który ze sposobów daje największe prawdopodobieństwo wylosowania trzech pełnych losów?
Zadanie 46
W ostrosłup prawidłowy czworokątny o krawędzi podstawy a i wysokości h wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe do płaszczyzny podstawy. Wyznacz stosunek objętości ostrosłupa do objętości sześcianu.
Zadanie 47
Pierwiastkiem wielomianu W(x) = x3 + ax2 + bx + c jest liczba r = - 2. Wyznacz współczynniki a, b, c oraz wiedząc, że liczby: 1, a, b, c tworzą ciąg geometryczny rozwiąż nierówność
Zadanie 48
Ankieta przeprowadzona w pewnej szkole na temat nowej matury dała następujące wyniki: 80% uczniów było przeciw wprowadzeniu nowej matury, wśród nich 60% to dziewczęta. Natomiast wśród zwolenników nowej matury dziewczęta stanowiły 40%. Spośród badanych wylosowano
jedną osobę. Oblicz prawdopodobieństwo zdarzenia, że jest to:
zwolennik nowej matury,
dziewczyna przeciwna nowej maturze
dziewczyna
chłopak popierający wprowadzenie nowej matury
Zadanie 49
Rozwiąż nierówność:
.
Zadanie 50
Dla jakich wartości parametru m równanie : x2 + (2m - 3)x + 2m + 5 = 0
ma dwa różne pierwiastki ujemne.
Zadanie 51
Oblicz sumę wszystkich liczb naturalnych mniejszych od 1000, które nie są podzielne przez 3.
Zadanie 52
Dla jakich wartości x liczby: 9,
,
są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz różnicę tego ciągu.
Zadanie 53
Trapez ABCD, w którym AB || CD jest wpisany w okrąg o promieniu R. Mając dane: |BD| = 14,kąt
BAD = 600,
oblicz pole i obwód trapezu oraz wyznacz długość R promienia okręgu.
Zadanie 54
Pole przekroju ostrosłupa prawidłowego trójkątnego płaszczyzną przechodzącą przez krawędź boczną i wysokość ostrosłupa wynosi
. Ściana boczna jest nachylona do podstawy pod kątem
. Oblicz objętość, pole powierzchni całkowitej tego ostrosłupa oraz objętość kuli wpisanej w ten ostrosłup.
Zadanie 55
Rzucono trzema kostkami do gry. Oblicz prawdopodobieństwo zdarzeń:
A - suma wyrzuconych oczek jest co najmniej równa 17,
B - iloczyn wyrzuconych oczek jest dokładnie równy 24.
Zadanie 56
W prostokątnym układzie współrzędnych podaj geometryczną interpretację zbiorów:
. Wykaż, że zbiór
jest jednoelementowy.
Zadanie 57
Dane są równania prostych: 3x + 5y -19 = 0 i 3x - 9y + 51 = 0 zawierających boki równoległoboku oraz równanie jednej z przekątnych:3x - 2y - 5 = 0.
wyznacz współrzędne wierzchołków równoległoboku,
napisz równanie drugiej przekątnej,
oblicz pole równoległoboku.
Zadanie 58
Suma trzech liczb tworzących ciąg arytmetyczny jest równa 15, jeżeli do drugiej z nich dodamy 1, a do trzeciej 5, to otrzymamy ciąg geometryczny. Wyznacz te liczby.
Zadanie 59
Podstawą graniastosłupa jest romb. Przekątne sąsiednich ścian bocznych wychodzących z jednego wierzchołka mają długości równe d i tworzą kąt
oraz są nachylone do podstawy pod kątem
. Oblicz objętość graniastosłupa.
Zadanie 60
Dla jakich wartości parametru m funkcja: y = (m2 + 5m - 6)x2 - (m - 1)x - 2 przyjmuje tylko wartości ujemne ?
Zadanie 61
Dla jakich wartości x liczby: log2, log(3x - 3), log(3x + 9) są kolejnymi wyrazami ciągu arytmetycznego?
Zadanie 62
Obwód równoległoboku wynosi 72 cm . Stosunek długości jego wysokości 5:7, a stosunek jego kątów wewnętrznych 1:2. Oblicz długości boków i wysokości równoległoboku.
Zadanie 63
Dla jakich wartości parametru m dwa różne pierwiastki równania:
spełniają warunek:
?
Zadanie 64
Wyznacz liczby całkowite należące do zbioru
, gdzie:
Zadanie 65
Zadrukowana część stronicy książki ma mieć pole 384 cm2. Marginesy boczne mają mieć szerokość 1 cm, a dolny i górny po 1,5 cm . Wyznacz wymiary stronicy tak, aby na produkcję książki zużyć jak najmniej papieru.
Zadanie 66
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens wynosi
. Wiedząc, że krawędź podstawy ma długość a oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Zadanie 67
W nieskończonym ciągu arytmetycznym (an) czwarty wyraz jest równy 4007, a siódmy wyraz wynosi 7004. O nieskończonym ciągu (bn) wiadomo, że jest monotoniczny i jego trzeci wyraz jest równy 1,25 i suma trzech pierwszych jego wyrazów jest równa 8,75. Z wyrazów ciągów (an) i (bn) utworzono nowy ciąg o wyrazie ogólnym
. Oblicz granicę ciągu cn.
Zadanie 68
W trójkącie prostokątnym równoramiennym ABC wierzchołek kąta ostrego A(3; 1). Przyprostokątna BC zawiera się w prostej o równaniu: x - y + 1 = 0. Napisz równania prostych zawierających pozostałe boki trójkąta.
Zadanie 69
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość
, a kąt między wysokościami sąsiednich ścian bocznych wychodzących z wierzchołka ostrosłupa ma 600. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
Zadanie 70
Turysta przebył pieszo trasę liczącą 600 km . Gdyby codziennie szedł o10 km więcej byłby w drodze o 5 dni krócej. Ile dni był turysta w drodze ?
Zadanie 71
Dla jakich wartości parametru m równanie: 2x + 2x - 1 + 2x - 2 + .... = 22x - 1 + m ma dwa różne rozwiązania ?
Zadanie 72
Zbadaj przebieg zmienności funkcji:
Zadanie 73
Dany jest trójkąt równoboczny ABC o boku a. Na bokach AB, BC, AC obrano odpowiednio punkty C1, A1, B1 tak, że:
. Punkty przecięcia się odcinków AA1, BB1, CC1 są wierzchołkami trójkąta PQR. Oblicz stosunek pola trójkąta PQR do pola trójkąta ABC.
Zadanie 74
Podstawą graniastosłupa prostego jest równoległobok ABCD, którego obwód wynosi 36 cm, wysokość graniastosłupa H = 8 cm . Przekątne graniastosłupa mają odpowiednio 18 cm i
cm . Oblicz pole równoległoboku ABCD.
Zadanie 75
Dany jest trójkąt prostokątny ABC, kąt ABC jest dwa razy większy od kąta CAB. Obwód koła wpisanego w ten trójkąt wynosi 2π.Z wierzchołka C poprowadzono prostą, która przecina przeciwprostokątną AB w punkcie D i tworzy z krótszą przyprostokątną kąt 300 . Oblicz pole koła opisanego na tym trójkącie, oraz stosunek długości odcinka
Zadanie 76
Napisz równanie stycznych do okręgu
i prostopadłych do prostej
.
Zadanie 77
Do urny, w której są dwie kule wrzucono białą kulę. Oblicz prawdopodobieństwo wyciągnięcia z urny kuli białej, jeśli wiadomo, że następujące zdarzenia są jednakowo prawdopodobne: przed wrzuceniem nie było w urnie kuli białej, była jedna kula biała, były dwie kule białe.
Zadanie 78
Wykaż, że styczne do wykresu funkcji
w punktach A(x0; 1) przecinają się w początku układu współrzędnych.
Zadanie 79
Punkty A (0; - 1) i B ( - 2; 1) należą do okręgu
Znajdź współrzędne takiego punktu C należącego do tego okręgu, by trójkąt ABC o podstawie AB był równoramienny.
Zadanie 80
Para liczb (x; y) jest rozwiązaniem układu równań
,Dla jakich wartości parametru m punkt P(x; y) należy do wnętrza koła o środku w początku układu współrzędnych i promieniu
.
Zadanie 81
Dane są krzywe o równaniach f(x) = x3 oraz g(x) = x2 - 4x + 4. Oblicz pole trójkąta wyznaczonego przez oś OX i styczne do tych krzywych w ich wspólnym punkcie.
Zadanie 82
Rozwiąż układ równań:
Zadanie 83
Dla jakich wartości parametru m suma sześcianów pierwiastków równania
jest równa - 26.
Zadanie 84
Rozwiąż równanie:
.
Zadanie 85
Dane są dwa wierzchołki trójkąta ABC: A( - 1; 1) oraz B(5; 7). Wysokości trójkąta przecinają się w punkcie P(3; 3). Wyznacz współrzędne punktu C oraz napisz równanie okręgu opisanego na trójkącie ABC.
Zadanie 86
Dla jakich wartości parametru m równanie
ma dwa różne pierwiastki rzeczywiste.
Zadanie 87
Dla jakich wartości parametru m równanie:
ma rozwiązanie.
Zadanie 88
Trzy pierwiastki wielomianu o współczynnikach całkowitych tworzą ciąg arytmetyczny. Ich suma wynosi 21, a iloczyn 315. Wykaż, że dla każdej całkowitej liczby nieparzystej wielomian ten przyjmuje wartość podzielną przez 48.
Zadanie 89
Dla jakich wartości parametru m punkt przecięcia się prostych:2x - 3my - 5 = 0 i 6x + 2y - 5 = 0 ma obie współrzędne dodatnie ?
Zadanie 90
Rozwiąż równanie:
.
Zadanie 91
Z cyfr 1, 2, 3, 4, 5 losujemy kolejno dwie bez zwracania i układamy z nich liczbę dwucyfrową (pierwsza wylosowana cyfra, to cyfra dziesiątek). Sprawdź czy zdarzenia: A - otrzymana liczba jest parzysta i B - otrzymana liczba jest podzielna przez 3 są niezależne.
Zadanie 92
W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość d i tworzy z przekątną podstawy kąt α.Oblicz objętość graniastosłupa.
Zadanie 93
W malejącym ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego wynosi 7, a suma kwadratów wyrazu drugiego i czwartego równa się 40. Ile wyrazów tego ciągu należy dodać, aby otrzymać - 64 ?
Zadanie 94
Trapez równoramienny opisany na okręgu o promieniu 2 cm, ma obwód 20 cm .Oblicz pole tego trapezu.
Zadanie 95
Wszystkie wyrazy pewnego ciągu arytmetycznego są dodatnimi liczbami całkowitymi. Suma wyrazu pierwszego i trzeciego wynosi 4 , a iloczyn tych wyrazów 3. Znajdź największą liczbę n, dla której spełniona jest nierówność: a1 + a2 + a3 + .... + an < 105.
Zadanie 96
Napisz równania stycznych do okręgu x2 + y2 - 6x + 4y - 12 = 0 poprowadzonych w punktach przecięcia się tego kręgu z prostą x - y + 2 = 0. Oblicz pole czworokąta, którego wierzchołkami są punkty styczności, środek okręgu oraz punkt przecięcia się stycznych.
Zadanie 97
Ciąg an jest określony wzorem: an = - 6n + 48. Dla jakich n zachodzi równość:
27an = a1 + a2 + a3 + … + an - 1 ?
Zadanie 98
Średnio dwie kobiety na 1000 i pięciu mężczyzn na 100 to daltoniści. Z grupy o jednakowej liczbie kobiet i mężczyzn wylosowano jedną osobę i okazało się, że jest ona daltonistą. Jakie jest prawdopodobieństwo, że jest to mężczyzna ?
Zadanie 99
Tworząca stożka ma długość l i jest nachylona do podstawy pod kątem α . Stożek przecięto płaszczyzną prostopadłą do wysokości tak, że pole powierzchni bocznej stożka zostało podzielone na dwie równe części. Oblicz wysokość otrzymanego stożka ściętego.
Zadanie 100
Dla jakich wartości parametru
najmniejsza wartość funkcji f(x) = x2 - 2x + cos2α + sinα + 3 jest równa 2 ?
Wskazówki do rozwiązania zadań
Zadanie 01
Zbiór A, to półpłaszczyzna ograniczona prostą y = - x + 1, zbiór B, to koło ośrodku S(
; 0) i promieniu r = 2. Różnica B - A jest odcinkiem koła (bez cięciwy).
(*):
Zbiory Am, to kwadraty o wierzchołkach (m ; 0), (0 ; m), ( - m ; 0), (0 ; - m).
Zbiory Bm, to koła o środku S(
; 0) i promieniu
, stąd
. Nierówność jest spełniona dla
i m
N.
Czyli m = 0.
Zadanie 02
Równanie ma 2 pierwiastki, gdy
czyli (k + 7 )2 - 4(k + 6) > 0, stąd
.Warunek zadania zapiszemy korzystając z wzorów Viete'a:
, stąd.
Odpowiedź:
Zadanie 03
Układ ma rozwiązanie dla m
6 :
,
.
,
.
Odpowiedź: m∈{ 1, 2, 3 }.
Zadanie 04
Dla
funkcja ma postać y = x2 + 2x - 1,dla
funkcja ma postać y = x2 - 2x + 1, dla
,
. Wierzchołek pierwszej paraboli W( - 1; - 2), drugiej P(1;0).
Przesuwając prostą y = m wzdłuż osi OY zauważamy, że równanie :
nie ma pierwiastków dla
,
ma jeden pierwiastek dla m = - 2,
ma dwa pierwiastki dla
,
ma trzy pierwiastki dla m = 0 lub
,
ma cztery pierwiastki dla
.
Zadanie 05
Układ ma rozwiązanie dla m
1:
,
Warunek zadania jest spełniony dla m = 3.
Zadanie 06
Przekątne kwadratu są prostopadłe, czyli prosta AC ma równanie
(zawiera dany punkt A). Przekątne przecinają się w punkcie S( - 1; - 2), długość odcinka
, stąd i z równania prostej AC mamy punkt C( - 3; - 1). Analogicznie:
oraz prosta BD pozwalają wyznaczyć B(0;0) i D( - 2; - 4).Pole kwadratu P = 10.
Zadanie 07
Środkiem okręgu jest punkt O(0;0). Prosta prostopadła do danej i przechodząca przez środek okręgu ma równanie y = x. Przecina okrąg w punktach A(2;2) i B( - 2; - 2), a prostą y = - x + 8 w punkcie C(4;4). Odległość
, zaś
.Stąd środkiem szukanego okręgu jest środek odcinka AC, punkt P(3;3), a promień jest połową jego długości:
.
Zadanie 08
Korzystając z określenia działania ! mamy:
,
Ciąg jest rosnący, 14 - ty wyraz jest równy
, a1 do a13 są mniejsze.
Zadanie 09
Podstawą ostrosłupa jest trójkąt równoboczny, czyli
. Wysokość ostrosłupa wraz z krawędzią boczną i odcinkiem równym
wysokości podstawy tworzy trójkąt prostokątny, w którym jest dany kąt
. Stąd wyznaczamy wysokość ostrosłupa
. Więc
. Podstawiając dane wielkości V = 18.
Zadanie 10
Dwa wierzchołki trójkąta wyznaczamy rozwiązując układ równań:
Stąd A(1;3) i B(4;0). trzeci to wierzchołek paraboli C(3;1). Wyznaczając długości boków trójkąta
,
,
sprawdzamy na podstawie twierdzenia Pitagorasa, że trójkąt jest prostokątny oraz obliczamy
.
Zadanie 11
Liczba x1 = P(A), gdzie
. Stąd x1 =
. Rozwiązaniem równania wykładniczego jest x2 = 4.Podstawiając x1 i x2 do W(x) otrzymujemy układ równań:
Stąd a = 2,5; b = - 7. Wielomian ma postać W(x) = x3 -2,5x2 -7x + 4 i jest podzielny przez trójmian (x -
)(x - 4) = x2 -4,5x + 2. Po wykonaniu dzielenia otrzymujemy trzeci pierwiastek x3 = - 2. Natomiast rozwiązaniem nierówności W(x) > 0 jest
.
Zadanie 12
Wiedząc, że
i S8 = 100 i a8 = 23 mamy a1 = 2 i r = 3.
Rozwiązując równanie na n - tą sumę ciągu arytmetycznego
obliczamy n = 16.
Zadanie 13
Rozwiązując układ równań
wyznaczamy dwa wierzchołki prostokąta A(0; - 5) i B(4;3), wierzchołek D leży na prostej prostopadłej do danej i przechodzącej przez punkt A, czyli prostej y = -
x - 5 i jest rozwiązaniem układu:
czyli D( - 4; - 3). Wyznaczamy długości boków prostokąta
,
i obliczamy pole P = 40.
Zadanie 14
Przekątna podstawy d = 4
, połowa przekątnej, krawędź boczna i wysokość ostrosłupa tworzą trójkąt prostokątny w którym jest kąt
i
, stąd h = 6.
.
Zadanie 15
Lewa strona jest sumą n wyrazów ciągu arytmetycznego, w którym a1 = 2, r = 3, Sn = 187 i x = an . Ze wzoru na sumę
wyznaczamy n = 11 czyli x = a11 = 32.
Zadanie 16
Obliczamy długość podstawy
. Piszemy równanie prostej AB : y = 2x - 3 i prostej do niej prostopadłej, przechodzącej przez C czyli prostej CD
.
Punkt D jest punktem przecięcia się tych prostych i końcem wysokości CD.
Z układu równań wyznaczamy D(3;3) i
.
.
Zadanie 17
Korzystając ze wzorów redukcyjnych obliczamy wartość a = 3, rozwiązaniem równania logarytmicznego jest b = 10. Szukane liczby to : 3, 4, 5, 6, 7, 8, 9 .
Zadanie 18
Równanie ma 2 pierwiastki gdy
,
czyli m < 4 . Warunek zadania można zapisać w postaci
czyli korzystając ze wzorów Viete'a
, stąd m > 3. Więc
.
Zadanie 19
Zbiór A jest zbiorem liczb spełniających nierówność wielomianową
(x - 3)(x - 2)(x + 2) = 0, czyli
,
aby wyznaczyć zbiór B należy nierówność wykładniczą sprowadzić do nierówności kwadratowej i otrzymamy
,zaś
. Stąd
.
Zadanie 20
Jest to równanie dwukwadratowe podstawiamy z = x2 i zakładamy warunki
, z1z2 > 0 i z1 + z2 > 0 oraz
. Po rozwiązaniu otrzymujemy
.
Zadanie 21
Z układu równań
otrzymujemy współrzędne punktu C(3;6).
Obliczamy długości boków trójkąta
,
i na podstawie twierdzenia Pitagorasa sprawdzamy, że jest to trójkąt prostokątny,
.
Średnica okręgu opisanego na trójkącie prostokątnym jest przeciwprostokątna trójkąta, stąd
, zaś środek ma współrzędne S(9;5), więc równanie okręgu ma postać:
(x - 9)2 + (y - 5)2 = 37.
Zadanie 22
Ze wzoru na wyrazy ciągu geometrycznego długości krawędzi można zapisać: a = a1, b = a2 = a1q, c = a3 = a1q2. Warunki zadania zapiszemy w postaci układu równań:
Odp. a = 5, b = 10, c = 20.
Zadanie 23
Rozwiązując równanie logarytmiczne: log2(x2 + 8x) + log2(x - 6) = 2log2(2x)otrzymujemy x = - 6 (sprzeczne) lub x = 8 Stąd a1 = log22 = 1 , a2 = log216 = 4 , a3 = log2128 = 7.
W szukanym ciągu a1 = 1 , r = 3 , Sn = 330 dla n = 15.
Zadanie 24
,
,
czyli
,
,
oraz zdarzenia A i B są zależne.
Zadanie 25
Korzystając z twierdzenia sinusów obliczamy pozostałe boki trójkąta podstawy,
,
gdzie
oraz wyznaczamy wysokość graniastosłupa
, pole podstawy
czyli
stąd mamy
oraz
.
Zadanie 26
Wysokość ściany bocznej dzieli ją na dwa trójkąty prostokątne,
korzystając z twierdzenia Pitagorasa oraz wzoru na pole trójkąta
wyliczamy długość krawędzi podstawy
oraz wysokość
ściany bocznej
, natomiast wysokość ostrosłupa
, czyli
.
Zadanie 27
Boki prostokąta mają długości h - wysokość walca i
- obwód
podstawy.
natomiast
. Objętość walca
. Dla podanych wartości
.
Zadanie 28
Funkcja osiąga ekstremum w miejscu zerowym pochodnej
f '( - 1) = 0 gdy m = - 3 i ma postać
x |
|
|
- 1 |
|
0 |
|
3 |
|
|
f'(x) |
|
+ |
0 |
- |
|
- |
0 |
+ |
|
f(x) |
|
|
|
|
9 |
|
0 |
|
|
Zadanie 29
x |
|
|
- 2 |
|
- 1 |
|
0 |
|
1 |
|
2 |
|
|
||
f'(x) |
|
+ |
|
+ |
|
+ |
0 |
- |
|
- |
|
- |
|
||
f(x) |
- 1 |
|
0 |
|
|
|
|
- 4 |
|
|
|
|
0 |
|
- 1 |
Zadanie 30
x |
|
|
0 |
|
2 |
|
|
|
f'(x) |
|
- |
0 |
+ |
|
- |
|
|
f(x) |
2 |
|
0 |
|
|
|
|
2 |
Równanie
ma :
2 rozwiązania dla
1 rozwiązanie dla k = 0
nie ma rozwiązania dla
Zadanie 31
Niech x - krawędź podstawy, h -wysokość prostopadłościanu,
wówczas : 8x + 4h = 72, stąd h = 18 -2x czyli V(x) = x2(18 - 2x).
Funkcja V(x) osiąga maksimum dla x = 6.
Zadanie 32
Przyjmując w danym trójkącie przyprostokątne r - promień podstawy stożka oraz h - wysokość stożka mamy r2 + h2 = 12 i
czyli
. Objętość jest maksymalna dla
i
.
Zadanie 33
Równanie logarytmiczne sprowadzamy do postaci x2 - 20x + 84 = 0 i otrzymujemy x1 = a1 = 6 oraz
x2 = a5 = 14, stąd różnica ciągu r = 2.Korzystając ze wzoru na sumę n wyrazów ciągu arytmetycznego wyznaczamy n = 10.
Zadanie 34
Patrz zadanie 15. Odpowiedź x = 33
Zadanie 35
Korzystając z własności ! wyraz ciągu zapiszemy w postaci:
i liman = - 2 czyli a = - 2.
Lewa strona danego równania jest sumą nieskończonego ciągu
geometrycznego o ilorazie
, czyli
więc
równanie przyjmuje postać:
. Rozwiązaniem
równania jest x = 2 czyli b = 2. Odcięta wierzchołka paraboli
należy do przedziału
jeżeli
oraz
więc
.
Zadanie 36
Z treści zadania a + b + c = 18 oraz b = 2a, więc c = 18 - 3a.
Objętość prostopadłościanu
,
objętość jest maksymalna dla a = 4, b = 8, c = 6.
Zadanie 37
Oznaczmy liczbę kolejnych obniżek - x. Wówczas (60 - x ), to zysk z jednego sprzedanego aparatu, natomiast (40 + x ), to ilość sprzedanych aparatów. Tworzymy funkcję f(x) = ( 60 - x )(40 + x ) i znajdujemy dla jakiego x ma ona największą wartość. Należy wyznaczyć współrzędne wierzchołka otrzymanej paraboli (położony jest najwyżej ) lub obliczyć pochodną.
Odp. x = 10, czyli cena powinna wynosić 160 - 10 = 150 zł.
Zadanie 38
Korzystając ze wzoru na sumę ciągu arytmetycznego tworzymy
układ równań:
i otrzymujemy a1 = - 6 i r = 2, dalej a7 = 6, a8 = 8, a9 = 10.
Otrzymany trójkąt jest prostokątny, promień okręgu opisanego, to połowa
przeciwprostokątnej R = 5, zaś promień okręgu wpisanego wyznaczamy
korzystając z faktu, że jego środkiem jest punkt przecięcia się
dwusiecznych, czyli podobieństwa odpowiednich trójkątów, r = 2.
Odpowiedź:
Zadanie 39
Niech a - krawędź podstawy, zaś h - wysokość graniastosłupa.
Ze związku między polami powierzchni mamy
, natomiast
przekątna
. Korzystając z twierdzenia cosinusów w trójkącie,
którego bokami są przekątne ścian bocznych wychodzące z jednego
wierzchołka i krawędź podstawy, otrzymujemy
.
Zadanie 40
Pochodna funkcji f”(x) = 3x2 + 2kx i f”( - 2) = 0, stąd k = 3.
Podstawiając do wzoru na funkcję i obliczając podobnie mamy m = - 4.
Funkcję można przedstawić w postaci f(x) = (x + 2)(x + 2)(x - 1).
Dla x = 0 ma min y = - 4.
Zadanie 41
Nierówność ze zbioru A można zapisać w postaci:
czyli
Z założeń do nierówności ze zbioru B mamy,
z rozwiązania
czyli
.
Odpowiedź:
.
Zadanie 42
Rozwiązaniem równania wykładniczego jest x = - 1 i x = 1, czyli p = 1.
Granica ciągu q = - 1, więc równanie przyjmie postać:
cos2x + sinx = 0.
Odpowiedź:
lub
lub
Zadanie 43
Dwusieczna dzieli bok BC trójkąta ABC na odcinki |BD| = 20 i |CD| = 15
oraz kąt prosty na dwa kąty po 450.
Korzystając z twierdzenia sinusów wyliczamy, że |AB| : |AC| = 4:3,
dalej z twierdzenia Pitagorasa mamy |AB| = 28 i |AC| = 21.
Dalej - patrz zadanie 38.
Zadanie 44
Prosta jest styczna jeżeli układ równań
ma jedno rozwiązanie. Jest nim punkt A(0 ;1).
Wyznaczamy środek okręgu S(2;0) i promień
. Środek S1(x ;y)
okręgu symetrycznego leży na prostej prostopadłej do danej i
przechodzącej przez punkt styczności oraz jego odległość od A wynosi
czyli jest rozwiązaniem układu równań:
Stąd S1( - 2 ;2), a więc okrąg ma równanie x2 + y2 + 4x - 4y + 3 = 0
Zadanie 45
zdarzenie A - wylosowanie trzech pełnych losów
- prawdopodobieństwo całkowite:
P(A) = P(A/B1)P(B1) + P(A/B2)P(B2) + P(A/B3)P(B3)
- zdarzenia niezależne:
Pi(1) - wylosowanie pełnego losu z i - tego pudełka,
P(A) = P1(1) P2(1) P3(1)
- prawdopodobieństwo jako stosunek ilości zdarzeń sprzyjających do wszystkich zdarzeń
Odpowiedź: Najkorzystniejszy jest pierwszy sposób losowania.
Zadanie 46
Przekrój osiowy bryły jest trójkątem równoramiennym o podstawie a i
wysokości h, w który wpisano kwadrat o boku b.
Z twierdzenia Talesa :
, gdzie
.
Czyli
, więc
Zadanie 47
W( - 2) = 4a - 2b + c - 8, oraz w danym ciągu a1 = 1, a = a2 = q, b = a3 = q2,
c = a4 = q3, stąd mamy q = 2, a = 2, b = 4, c = 8.
Rozwiązaniem nierówności jest
Zadanie 48
Zadanie można łatwo rozwiązać za pomocą grafu, lub ze wzorów
prawdopodobieństwo z definicji klasycznej P(A) = 0,2
ze wzoru na prawdopodobieństwo warunkowe
ze wzoru na prawdopodobieństwo całkowite
jak punkt b: P(A) = 0,12.
Zadanie 49
Z założenia o istnieniu logarytmu
mamy x < 4
z rozwiązania nierówności logarytmicznej
mamy
czyli
.
Zadanie 50
Warunki zadania:
dwa pierwiastki gdy
tego samego znaku gdy
dwa pierwiastki ujemne gdy
Odpowiedź:
Zadanie 51
Niech S oznacza szukaną sumę, S1 - sumę wszystkich liczb naturalnych mniejszych od 1000, zaś S2 - sumę wszystkich liczb naturalnych mniejszych od 1000 i podzielnych przez 3.
Wówczas S = S1 - S2 oraz
,
,
Odpowiedź: S = 332667.
Zadanie 52
Zapisujemy warunek. by liczby tworzyły ciąg arytmetyczny w postaci równania wykładniczego:
, wprowadzamy za 2x nową zmienną i rozwiązujemy otrzymane równanie kwadratowe.
Odp.
, lub
oraz
,
Zadanie 53
Korzystamy z twierdzenia cosinusów w trójkącie ABD do wyznaczenia ramienia |AD| = 10, a potem podstawy |AB| = 16. Prowadzimy wysokość DE i wyznaczamy ją z trójkąta AED.
oraz odcinek |AE| = 5,czyli podstawa |CD| = 6. Pole trapezu
, a obwód Ob = 42. Promień R można wyznaczyć korzystając z trójkątów AGO i DFO, gdzie O - środek okręgu, a FG wysokość trapezu przechodząca przez środek O,
.
Zadanie 54
Przekrój jest trójkątem, o bokach hp - wysokość trójkąta podstawy, hs - wysokość ściany bocznej, b - krawędź boczna. Wysokość w tym trójkącie jest jednocześnie wysokością H ostrosłupa. Korzystając z danego pola trójkąta i związków trygonometrycznych mamy:
,
, H = 6 oraz z faktu, że podstawa jest trójkątem równobocznym krawędź podstawy a = 12. Objętość ostrosłupa
, pole
. Promień kuli wpisanej w ostrosłup obliczamy korzystając z podobieństwa trójkątów: r = 2 ( w przekroju koło jest styczne tylko do dwóch boków trójkąta hp i hs).
Zadanie 55
Zdarzeń elementarnych jest tu
,
,
Do zbioru B należą wszystkie trójki złożone z liczb 1,4,6 oraz 2,3,4
i 2,2,6. Jest ich
.
,
.
Zadanie 56
Geometrycznym przedstawieniem zbioru A jest parabola o wierzchołku
W(1; - 1) wraz z wnętrzem, natomiast dla zbioru B półpłaszczyzna
ograniczona prostą y = - 2x + 2, wraz z tą prostą.
Układ równań:
ma tylko jedno rozwiązanie, czyli
zbiór
jest jednoelementowy, jest to punkt P(2; - 2)
Zadanie 57
Rozwiązując odpowiednie układy równań wyznaczamy współrzędne
wierzchołków: A( - 2; 5), B(3;2), D(7;8) .Piszemy równani dwóch
pozostałych prostych zawierających boki równoległoboku i wyznaczamy
punkt C(12;5). Szukana przekątna AC ma równanie y = 5.
Pole równoległoboku P = 42.
Zadanie 58
Należy rozwiązać układ równań:
Odp. x = 12, y = 5, z = - 2, lub x = 3, y = 5, z = 7.
Zadanie 59
Z trójkąta o bokach a - bok rombu, h - wysokość graniastosłupa i d
wyznaczamy:
,
. Z trójkąta o bokach d, d, x,
gdzie x - przekątna rombu, wyznaczamy
, druga przekątna
rombu
. Objętość graniastosłupa:
Zadanie 60
Warunki zadania są spełnione gdy:
a < 0, czyli gdy
, czyli gdy
.
Odpowiedź:
.
Zadanie 61
Należy zapisać warunek na ciąg arytmetyczny w postaci równania
logarytmicznego: log(3x + 9) - log(3x - 3) = log(3x - 3) - log2,
Założenie 3x - 3 >0, czyli x > 1,
Rozwiązaniem równania jest x = 2.
Zadanie 62
Kąty równoległoboku mają odpowiednio
. Wprowadźmy
oznaczenia: boki równoległoboku a i b, wysokość opuszczona na bok
a - h, na bok b - H. Wówczas: a + b = 36,
,
oraz
. Stąd: a = 21, b = 15,
,
.
Zadanie 63
Po sprowadzeniu obu stron równania do wspólnej podstawy i
uporządkowaniu otrzymamy równanie kwadratowe:
, ma ono dwa pierwiastki gdy
.
Warunek zadania rozwiązujemy po przekształceniu do postaci:
korzystając z wzorów Viete'a.
Odpowiedź: m = - 3.
Zadanie 64
Zbiór A, to rozwiązanie nierówności wielomianowej,
.
Zbiór B, to rozwiązanie nierówności logarytmicznej wraz z założeniem
o istnieniu logarytmu,
.
Zbiór C, to:
.
Oraz:
Odpowiedź: Szukane liczby, to: - 1, 0, 3.
Zadanie 65
Niech x - jeden bok zadrukowanej części, y - drugi bok,
wówczas
. Wymiary stronicy zapiszemy jako funkcję:
f(x,y) = (x + 2)(y + 3), czyli inaczej:
. Pochodna funkcji:
.
Funkcja ta osiąga minimum dla x = 16.
Odpowiedź: Wymiary stronicy, to x + 2 = 18 i y + 3 = 27.
Zadanie 66
Podstawą ostrosłupa jest trójkąt równoboczny o boku a,
wysokość podstawy
oraz
, gdzie H - wysokość
ostrosłupa, stąd
. Z tw. Pitagorasa wysokość ściany bocznej
, czyli
.
Odpowiedź:
oraz
Zadanie 67
W ciągu arytmetycznym:
, czyli a1 = 1010 i r = 999.
Dowolny wyraz an = 11 + 999n.
Analogicznie w ciągu geometrycznym:
, stąd
lub
ale ta odpowiedź jest sprzeczna
z założeniem o monotoniczności ciągu więc b1 = 5.
Dowolny wyraz
. Stąd
.
Odpowiedź: dla
jest
, czyli
.
Zadanie 68
Równanie prostej AC prostopadłej do BC i przechodzącej przez punkt A:
y = - x + 4.
Współrzędne punktu C stanowią rozwiązanie układu tych dwóch prostych:
. Trójkąt jest równoramienny, więc |AC| = |BC| oraz punkt B leży
na prostej BC, czyli y = x + 1. Stąd B1(0;1) lub B2(3;4). Prosta AB ma
równanie: y = 1 lub x = 3.
Odpowiedź: prosta BC: y = x + 1, prosta AC: y = - x + 4,
prosta AB: y = 1 lub x = 3.
Zadanie 69
Podstawą trójkąta, którego ramionami są wysokości sąsiednich ścian
bocznych jest odcinek łączący środki krawędzi podstawy a o długości
, jest to trójkąt równoboczny stąd wysokość ściany bocznej
. Z trójkąta utworzonego przez wysokość ściany bocznej, połowę
krawędzi podstawy i krawędź boczną wyznaczymy: a = 12 i
.
Wysokość ostrosłupa H wyznaczamy z trójkąta o bokach H, hs,
: H = 6.
Odpowiedź: V = 288,
Zadanie 70
Niech x - liczba dni w trasie, y - liczba przebytych dziennie kilometrów.
Odpowiedź: x = 20 dni.
Zadanie 71
Lewa strona równania jest sumą ciągu geometrycznego zbieżnego o
ilorazie
i wyrazie a1 = 2x.
więc równanie po
uporządkowaniu ma postać:
.
Po podstawieniu z = 2x mamy:
.
Aby spełniony był warunek zadania to równanie musi mieć dwa dodatnie
pierwiastki czyli:
, z1 + z2 >0 oraz z1z2 >0.
Odpowiedź:
.
Zadanie 72
x |
|
|
|
|
- 2 |
|
0 |
|
2 |
|
|
|
|
f'(x) |
- |
- |
- |
- |
0 |
+ |
+ |
+ |
0 |
- |
- |
- |
- |
f(x) |
|
|
0 |
|
- 4 |
|
0 |
|
4 |
|
0 |
|
|
Zadanie 73
Z twierdzenia cosinusów wyznaczamy bok |CC1| w trójkącie ACC1.
. Należy zauważyć, że trójkąty ACC1 oraz AC1P są podobne,
oraz AC = a,
, korzystając z podobieństwa tych trójkątów
mamy:
czyli
oraz
czyli
.
Stąd obliczamy bok trójkąta PQR: b = |CC1| - |AP| - |PC1| czyli
.
Stosunek pól tych trójkątów
.
Zadanie 74
Oznaczmy: boki równoległoboku a i b, wysokość h, przekątne
graniastosłupa c i d oraz przekątne równoległoboku x i y. Wówczas mamy:
a + b = 18, h = 8, c = 18,
. Z trójkątów o bokach h, c, x
oraz h, d, y obliczamy
i
. Z twierdzenia cosinusów dla
trójkątów o bokach a, b, x oraz a, b, y i zależności a = 18 - b, wyliczamy:
a = 8 , b = 10 (lub a = 10, b = 8) oraz
( gdzie
jest ostrym kątem
równoległoboku). Z jedynki trygonometrycznej
, czyli pole
równoległoboku
Zadanie 75
W danym trójkącie kąty mają odpowiednio
i
, promień
koła wpisanego r = 1.
Możemy boki trójkąta zapisać w postaci: a = x + r , b = y + r , c = x + y,
gdzie x i y to odcinki wyznaczone przez promienie prostopadłe do boków
trójkąta. Wówczas (x + 1)2 + (y + 1)2 = (x + y)2 oraz
.
Stąd mamy:
,
oraz
,
,
. Promień koła opisanego
, pole
.
Trójkąt BDC jest podobny do trójkąta ABC stąd
. natomiast
więc
.
Zadanie 76
Prosta prostopadła do danej ma równanie
. Po wstawieniu równania
prostej do równania okręgu otrzymujemy równanie kwadratowe z parametrem b,
które ma jedno rozwiązanie dla b1 = 4 i b2 = - 6, czyli szukane styczne to:
,
.
Zadanie 77
Korzystamy, ze wzoru na prawdopodobieństwo całkowite, przy czym:
P(B1) = P(B2) = P(B3) =
.
Natomiast P(A/B1) =
, P(A/B2) =
, P(A/B3) = 1
Czyli P(A) =
.
Zadanie 78
Wyznaczamy punkty styczności jako rozwiązanie równania :
;
Otrzymujemy A1(1;1), A2( - 1;1). Równanie stycznych piszemy wg. wzoru:
y - y1 = f `(x1)(x - x1) i otrzymujemy dwie styczne y = x oraz y = - x, które
przecinają się w początku układu współrzędnych.
Zadanie 79
Współrzędne punktu C(x; y) wyznaczamy rozwiązując układ równań:
i otrzymujemy :
oraz
.
Zadanie 80
Rozwiązaniem układu równań jest para:
. Punkt P(x; y) należy do koła o promieniu
jeżeli
. Odpowiedź:
.
Zadanie 81
Punkt wspólny krzywych: A(1; 1).
Styczna do funkcji f(x) ma równanie: y = 3x - 2.
Styczna do funkcji g(x) ma równanie: y = - 2x + 3.
Wierzchołkami trójkąta są punkty:
.
Odpowiedź: Pole trójkąta
.
Zadanie 82
Rozpatrujemy dwa przypadki:
I
wówczas y = x2 - 2x + 1.
II
wówczas y = - (x2 - 2x) + 1.
Odpowiedź:
lub
lub
.
Zadanie 83
Równanie ma dwa pierwiastki dla
.
Korzystamy z zależności:
oraz wzorów Viete'a.
Odpowiedź: m = 3,5
Zadanie 84
Dla
i
wyrażenie pod logarytmem jest sumą nieskończonego
ciągu geometrycznego. Z założenia wynika też
.
Po uproszczeniu równani ma postać
.
Odpowiedź: x = 1.
Zadanie 85
Piszemy równania prostych: BP:
, AP:
oraz
prostych do nich prostopadłych odpowiednio: AC:
i BC:
. Wyznaczamy punkt C z układu prostych AC i BC.
C(11; 5). Równanie okręgu:
.
Zadanie 86
Wprowadzamy nową zmienną
oraz określamy warunki zadania:
1)
2)
3)
4)
.
Odpowiedź:
Zadanie 87
Po przekształceniu i uporządkowaniu równanie ma postać
.
Dla m = - 1 jest sprzeczne, równanie ma rozwiązanie gdy
.
Odpowiedź:
Zadanie 88
Pierwiastkami tego wielomianu są liczby 5, 7, 9. Można go więc zapisać w
postaci: W(x) = (x -5)(x - 7)(x - 9)P(x), gdzie P(x) dowolny wielomian.
Dla dowolnej liczby nieparzystej x trzy pierwsze czynniki są kolejnymi
liczbami parzystymi, a ich iloczyn jest zawsze podzielny przez 48.
Zadanie 89
Układ ma rozwiązanie dla
,
,
.
Warunek zadania jest spełniony dla
.
Zadanie 90
cos2x = 1 - sin2x; wprowadzamy nową zmienną
i
,
po rozwiązaniu równania kwadratowego i podstawieniu mamy:
.
Zadanie 91
,
,
, czyli zdarzenia nie są niezależne.
Zadanie 92
Przekątna podstawy
, pole podstawy,
.
Krawędź podstawy
i wysokość graniastosłupa
(z tw. Pitagorasa)
. Stąd objętość
.
Zadanie 93
Ciąg arytmetyczny jest malejący jeżeli jego różnica jest liczbą ujemną.
Z rozwiązania układu równań
mamy r = 4 i a1 = 6.
Dalej ze wzoru na sumę ciągu arytmetycznego otrzymujemy n = 8.
Zadanie 94
W czworokącie opisanym na okręgu sumy długości przeciwległych boków
są równe, czyli a + b = 2c.
Odpowiedź : Pole trapezu P = 20 cm2.
Zadanie 95
Z układu równań
wyznaczamy a1 = 1 oraz r = 1.
Po rozwiązaniu nierówności Sn < 105 otrzymujemy n < 14.
Odpowiedź : Największą liczbą spełniająca nierówność jest n = 13.
Zadanie 96
Z układu równań
wyznaczamy punkty styczności:
A(0; 2) i B( - 1; 1), środek okręgu ma współrzędne S(3; - 2), styczne są prostopadłe
do prostych AS i BS i mają równania :
oraz
, styczne
przecinają się w punkcie
. Pole czworokąta ABSO jest sumą pól
przystających trójkątów prostokątnych ASO i BSO i wynosi
.
Zadanie 97
Ze wzoru ogólnego wyznaczamy a1 = 42, a2 = 36, czyli r = - 6.
Prawa strona równania jest sumą n - 1 wyrazów ciągu czyli ma postać
oraz
i
Podstawiając do danej równości otrzymujemy n = 7 lub n = 64.
Zadanie 98
Korzystamy ze wzoru na prawdopodobieństwo warunkowe
gdzie
- wybrano mężczyznę daltonistę natomiast B - wybrano daltonistę
.
Zadanie 99
Niech l - tworząca stożka, r - promień podstawy, h - wysokość. Natomiast
L, R, H - niech będą odpowiednimi wielkościami w małym stożku powstałym
po cięciu przy wierzchołku. Wówczas
czyli rl = 2RL oraz
i
Stąd
więc
, analogicznie
i
oraz szukana wysokość stożka ściętego hs = h - H, więc po podstawieniu
mamy hs =
.
Zadanie 100
W danym równaniu a = 1, b = 2,
, najmniejsza wartość
funkcji jest równa
, po podstawieniu otrzymujemy równanie
trygonometryczne:
i korzystając ze wzoru na funkcje
wielokrotności kąta
mamy dalej równanie
Odpowiedź:
lub
lub
.
35
Wyszukiwarka