Zadania na ćwiczenia 2

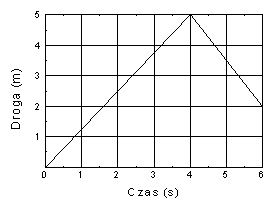
Na rysunku po prawej przedstawiono wykres zależności drogi od czasu dla pewnego ciała. Oblicz prędkość ciała w trzeciej i piątej sekundzie ruchu oraz prędkość średnią dla całego ruchu.
Tramwaj rusza z miejsca z przyspieszeniem 0,3 m/s2. W ciągu jakiego czasu przejedzie on pierwszy oraz dziesiąty metr swojej drogi? Jaką prędkość osiągnie na końcu dziesiątego metra?
Cząstka porusza się ruchem prostoliniowym wzdłuż osi OX. Wiadomo, że ![]()
gdzie A = 3 m/s, B = 2 m/s2 i C = 1 m/s3. Obliczyć prędkość oraz przyśpieszenie tej cząstki po pierwszej, drugiej i trzeciej sekundy ruchu. Obliczyć średnią prędkość oraz średnie przyśpieszenie tej cząstki w czasie pierwszej, drugiej i trzeciej sekundy ruchu.
Z wieży o wysokości h rzucono jednocześnie dwa ciała: jedno pionowo w górę z szybkością v1 i drugie w dół z szybkością v2. Obliczyć odstęp czasu Δt oddzielający momenty upadku tych ciał o ziemię. Opór powietrza zaniedbać.
Ciało zostało wyrzucone z wieży o wysokości H=20 m pod kątem od poziomu w górę, z prędkością początkową v=30 m/s. Zaproponować odpowiedni układ odniesienia. Wyrazić w tym układzie warunki początkowe w postaci wektorowej. Podać wektorowe równanie toru. Zapisać warunek upadku ciała na ziemię. Znaleźć równanie krzywej opisującej tor, obliczyć maksymalną wysokość oraz zasięg ruchu.
Pocisk wystrzelono z szybkością v0 pod kątem θ do poziomu. Po czasie t0 = 10 s pocisk uderzył w Ziemię w odległości l = 2 km od miejsca wystrzału. Znaleźć v0, θ i maksymalną wysokość h, na jaką pocisk wzniósł się w czasie lotu. Opór powietrza zaniedbać, a przyśpieszenie ziemskie przyjąć równe g = 10 m/s2.
Opisać wektorowo ruch “jednostajny” po okręgu o promieniu r = 3 m z częstotliwością 1/20 s-1 w układzie współrzędnych związanym z punktem na okręgu. Znaleźć w tym układzie wektory położenia, prędkości i przyspieszenia w chwili t1 = 5 s, jeśli w chwili t0=0 s ciało znajdowało się w początku układu współrzędnych. Znaleźć wektory położenia, prędkości i przyspieszenia średniego w przedziale od t0 do t1. Wyniki zobrazować graficznie.
Opisać wektorowo ruch (i) kamyka który wbił się w bieżnik opony 155x13 (promień r=32 cm ) oraz (ii) ruch końca wentyla tej opony w układzie współrzędnych (nieruchomym) związanym z drogą, dla samochodu poruszającego się ze stałą prędkością v= 60 km/godz. (Wskazówka: ruch ten jest złożeniem ruchu obrotowego i postępowego, krzywa opisująca tor nazywa się cykloidą). Naszkicować tor ruchu. Obliczyć a i v. Dla przypadku (i) przedyskutować kiedy prędkość i przyspieszenie są najmniejsze i największe.