Dawid Trzcionka

91610

WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH

-SEMINARIUM-

SEM. ZIMOWY 2000/2001

Prowadzący

Dr inż. Wojciech J. Krzysztofik

ZADANIE 3/1

Sygnał f(t)=4sin4π*10³t [V] moduluje częstotliwościowo falę nośną c(t)=6cos5π*10⁶t [V]. Szerokość zmodulowanego s_FM(t) wynosi B=16kHz. Obliczyć wartość stałej k funkcjonału modulacji. O ile prążków bocznych poszerzy się pasmo, gdy częstotliwość sygnału modulującego zmaleje dwukrotnie?

Wstęp teoretyczny

Sygnał zmodulowany

s(t)=c(t)m[f(t)]

gdzie

c(t) - funkcja nośna

m[f(t)] - funkcjonał modulacji

Funkcjonał modulacji ma postać

Zatem wyrażenie na sygnał zmodulowany przyjmuje postać

s_FM(t)=A₀cosΦ_FM(t)=A₀cos(ω₀t+*Φsinωt).

*f=*ω/2π=kA dewiacja częstotliwości jest ustalona

*Φ=*ω/ω dewiacja fazy zależy od częstotliwości sygnału modulującego

Po wprowadzeniu pojęcia wskaźnika modulacji β

β=*ω/ω=*f/f przy modulacji FM

wyrażenie na sygnał zmodulowany kątowo zapisujemy

s_FM(t)=A₀cos(ω₀t+βsinωt).

Rozwiązanie zadania

Dane: Szukane:

f(t)=4sin4π*10³t [V] k=?

c(t)=6cos5π*10⁶t [V]

B=16kHz dla s_FM(t)

ω=2πf

f_f=10³ [Hz] - częstotliwość sygnału modulującego

f_c=10⁶ [Hz] - częstotliwość fali nośnej

β=*ω/ω=kA/ω

Szerokość pasma sygnału FM można oszacować

B=2f(β+1)=2f(kA/ω+1).

Podstawiając wartości

ω=4π*10³

A=4

f=ω/2π=2*10³ Hz

B=16kHz=16*10³ Hz

Otrzymujemy

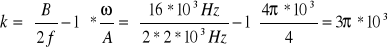
k=3π*10³

Jeśli przyjąć, że widmo sygnału jest określone przez wszystkie prążki, których amplituda jest większa niż 5% amplitudy fali nośnej przed modulacją, to między liczbą par uwzględnionych prążków a dewiacją fazy zachodzi następująca zależność

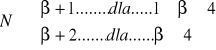
Dla naszych wartości mamy

Korzystamy z pierwszego przybliżenia

N=β+1=3+1=4

Jeżeli częstotliwość sygnału modulującego zmaleje dwukrotnie:

N=β+2=6+2=8

Odp. Jeżeli częstotliwość sygnału modulującego zmaleje dwukrotnie, to liczba prążków wzrośnie dwukrotnie.