Rozwiązywanie układów równań metodą operacji elementarnych (na wierszach)

(metoda Jordano-Gaussa).

Dokonując operacji elementarnych na układzie

Ax=b

możemy go przekształcić w układ równoważny

Cx=d,

gdzie macierz C jest macierzą bazową (wierszowo zredukowaną macierzy A)

Układ Cx=d nazywamy postacią bazową układu Ax=b.

Postać bazowa Cx=d jest jednoznacznie wyznaczoną przez macierz blokową E=[ Cd ], którą otrzymujemy dokonując operacji elementarnych na wierszach macierzy uzupełnionej A^U (=[ Ab]). Z postaci bazowej układu można natychmiast odczytać rozwiązanie układu lub stwierdzić, że układ jest sprzeczny.

Jeżeli układ równań jest nieoznaczony (tzn. rz(A) < n), to wśród rozwiązań wyróżniamy tzw. rozwiązanie bazowe.

Rozwiązaniem bazowym układu równań liniowych nazywamy takie rozwiązanie, w którym wszystkie zmienne swobodne (niebazowe) są równe zeru.

Przykładowe zadanie:

Rozwiązanie układu równań metodą operacji elementarnych

Jordano-Gaussa

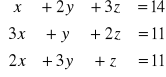
Przekształcamy związaną z układem macierz współczynników

W₂^' = W₂ + (-3)W_{1 ;} W₃^' = W₃ + (-2)W₁

=>
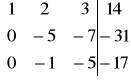
W₂^' =W₂+(-6)W₃

=>
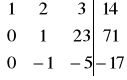
W₁^' = W₁ + (-2)W_{2 ;} W₃^' = W₃ +W₂

=>
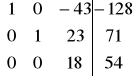
W₃^' =W₃:18

=>
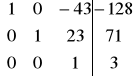
W₁^' = W₁ + 43W_{3 ;} W₂^' = W₂ +(-23)W₃

=>
=>