1. Opisać układ Lagrange'a, prędkość i przyśpieszenia w tym układzie.

Metoda Lagrange'a - jedna z metod badania stosowana przy opisie ruchu płynu. Metoda Lagrange'a nazywana tez metodą analizy wędrownej, polega na badaniu i opisie własności fizycznych poruszającego się pewnego elementu płynu. W tym celu niezbędne jest dokonanie wyboru cząstki, np. przez opisanie współrzędnych położenia a,b,c dla chwili to, a następnie jej śledzenie w kolejnych chwilach t. W wyniku zastosowanej metody otrzymuje się opis ruchu płynu w postaci f=f(a,b,c,t), gdzie f jest współrzędną położenia lub własnością płynu w chwili t.

Zmiennymi Lagrange'a w przestrzeni nazywa się czwórkę liczb a,b,c,t, z których trzy pierwsze opisują jednoznacznie wytypowany element płynu.

Współrzędne położenia elementu płynu w kolejnych chwilach czasowych, wyrażające parametryczne równanie toru cząstki, określają następujące równania

x=x(a,b,c,t) y = y(a,b,c,t) z= z(a,b,c,t)

Składowe prędkości poszczególnych elementów płynu wynoszą

Vx=δ x/ δt Vy= δy/ δt Vz= δz/ δt

a składowe przyśpieszeń

ax= δ²x/ δt² ay= δ²y/ δt² az= δ²z/ δt²

inne parametry stanu ruchu płynu, np. gęstość i ciśnienie wyraża się zgodnie ze wzorem zależnościami

ρ= ρ(a,b,c,t) p=p(a,b,c,t)

System zmiennych Lagrange'a pozwala śledzić zmiany położenia poszczególnych obiektów np. balonów meteorologicznych w atmosferze.

2. Opisać układ Eulera, prędkości i przyśpieszenia w tym układzie.

Metoda Eulera - jedna z metod badania stosowana przy opisie ruchu płynu.

Metoda Eulera, nazywana tez metoda analizy lokalnej, opisuje zmiany wielkości fizycznych płynu w poszczególnych punktach przestrzeni, w której odbywa się ruch. Metoda ta polega więc na badaniu pól wielkości fizycznych, a nie indywidualnych cech poszczególnych elementów płynu. W wyniku jej zastosowania otrzymuje się opis ruchu w postaci funkcji

Vx=vx(x,y,z,t) Vy=Vy(x,y,z,t) Vz=Vz(x,y,z,t)

ρ = ρ(x,y,z,t) p=p(x,y,z,t)

gdzie x,y,z,t są nazywane zmiennymi Eulera.

Zamiast x,y,z można wprowadzić dowolny układ współrzędnych przestrzennych, np. walcowy, sferyczny.

Ze zmiennych Eulera korzysta się przy analizie ruchu płynu, np. w przewodach.

Dla znanego pola prędkości, przyśpieszenie elementu płynu wyrażone w zmiennych Eulera należy zapisać jako:

a=dv(x,y,z,t)/dt = δv/ δt+ δv/ δx dx/dt+ δv/ δy dy/dt+ δv/ δz dz/dt

jeżeli Vx=dx/dt Vy=dy/dt Vz=dz/dt

to otrzymuje się

dv/dt= δv/ δt+ Vx δv/ δx+Vy δv/ δy+ Vz δv/ δz

Wielkość dv/dt jest nazywana pochodną substancjalną prędkości i wyraża rzeczywiste przyśpieszenie cząstki δv/ δt jest pochodną lokalną, a suma trzech pozostałych członów - pochodną konwekcyjną związaną z przesunięciem elementu po jego torze.

3. Linia prądu i tor, kiedy one są tożsame?

Linią prądu nazywa się linię pola wektorowego prędkości, która w danej chwili w każdym swym punkcie jest styczna do wektora V odpowiadającego temu punktowi. Jeżeli element długości tej linii ds. ma składowe dx,dy,dz to równanie linii prądu wyznaczone z warunku styczności można zapisać jako

dx/ Vx(x,y,z,t) = dy/ Vy(x,y,z,t) = dz/Vz(x,y,z,t)

Czas w powyższych zależnościach odgrywa rolę parametru

Torem nazywa się drogę, którą opisuje dany element płynu. Jeżeli w polu prędkości elementarne przesunięcie cząstki ds. ma składowe dx,dy,dz to różniczkowe równania form można zapisać jako

dx=Vxdt, dy=Vydt, dz=Vzdt

Linia prądu i tor są tożsame w ruchu ustalonym. W przepływie ustalonym tory i linie prądu pokrywają się.

4. Definicja wydatku (przepływu) dla strumienia i strugi

Struga - jest to zespół linii prądu zawartych w rurce prądu o nieskończenie małym przekroju dA

Strumień - stanowi zespół strug o skończonym przekroju A

5. Tensor prędkości deformacji

Ɛx Ɵz Ɵy

Td= Ɵz Ɛy Ɵx

Ɵy Ɵx Ɛz

otrzymujemy go w wyniku rozkładu tensora prędkości względnej

T=

tensor prędkości względnej rozkłada się na tensor prędkości deformacji i na tensor wiru

6. Tensor naprężeń

Naprężenie oderwane od kierunku powierzchni przekroju może być opisane przez tensor naprężenia σ. Z prawa zachowanie momentu pędu wynika, że tensor naprężenia jest symetryczny

σx τxy τxz

σ= τxy σy τyz

τxz τyz σz

gdzie: σx, σy, σz - składowe normalne, τxy, τxz, τyz - składowe ścinajace

7. Lepkość cieczy w ujęciu makroskopowym i mikroskopowym, naprężenia styczne w ruchu laminarnym

Lepkosć - zdolność płynu do przenoszenia naprężeń stycznych przy wzajemnym przemieszczeniu jego elementów z różnymi prędkościami.

Podczas przepływu płynu lepkiego pojawiają się naprężenia styczne skierowane przeciwnie do kierunku ruchu. Powodują one powstanie sił nazywanych ogólnie oporami tarcia.

Ruch elementów płynu wywołany pewnym zaburzeniem ma charakter pulsacji. Reynolsd wykazał, że energia tego ruchu jest wzmacniana przez energię ruchu podstawowego, a jednocześnie wytracana w postaci ciepła na skutek działania lepkości. W ruchu laminarnym energia przekazywana ruchom pulsacyjnym jest nieduża i przepływ jest stateczny. W przepływie tym poszczególne warstwy (rurki prądu) stanowią pewne bariery, poprzez które nie zachodzi wymiana płynu w skali makroskopowej. Możliwa jest natomiast wymiana masy w skali mikroskopowej, wynikająca z bezwładnego ruchu cząsteczek (molekuł). Dzięki wymianie masy (w gazach) oraz siłom spójności (w cieczach) warstwy poruszające się z różnymi prędkościami oddziałują na siebie naprężeniami stycznymi, które określone są wzorem Newtona τ=T/A = +-μdV/dn

8. Ruch turbulentny - definicja, liczba Reynoldsa, naprężenia styczne w ruchu turbulentnym

Przepływ turbulentny - Jest określeniem ruchu płynu, odznaczającego się niestacjonarnością, poszczególne warstwy płynu mieszają się ustawicznie, a poszczególne elementy płynu wykonują obok ruchu głównego również nieregularne ruchy w innych kierunkach.

Na podstawie wyników własnych badań Reynolds ustalił, że zmiana charakteru przepływu zależy od wartości bezwymiarowej liczby (nazwanej później liczbą Reynoldsa) i oznaczanej symbolem Re:

Liczba Reynoldsa wyraża stosunek składowej konwekcyjnej siły bezwładności do siły tarcia w płynie.

Dla odpowiednio dużych wartości liczby Reynoldsa, energia przekazywana z ruchu podstawowego do pulsacyjnego jest większa niż ciepło wytwarzane na skutek tarcia. W efekcie przepływ traci stateczność, zaburzenia wzmagają się i rozprzestrzeniają, co prowadzi do nowej struktury przepływu, zwanej turbulentną. Istotą ruchu turbulentnego jest brak wewnętrznej stabilności przepływu. Występują w nim przypadkowe nieregularne zaburzenia - pulsacje, które powodują że ruch wewnątrz tego obszaru jest zmienny w czasie. Przepływ turbulentny charakteryzuje się intensywną wymianą masy oraz pędu między poszczególnymi warstwami. Występują tu naprężenia styczne tał wywołane zarówno lepkością newtonowską τL (naprężenia lepkie), jak i ruchem pulsacyjnym τT (naprężenia turbulentne).

Liczbę Reynoldsa odpowiadającą przejściu przepływu laminarnego w turbulentny nazywamy krytyczną liczbą Reynoldsa - Re_kr.

9. Równanie Bernoulliego dla cieczy idealnej

Równanie Bernoulliego - równanie opisujące przepływ niezaburzony (laminarny) cieczy doskonałej wewnątrz rury o zmiennym przekroju i położenu.

ρgh=0,5ρV^2+p=const.

Gdzie: ρ- gęstość cieczy, h- wysokość środka przekroju nad poziomem odniesienia, V- prędkość dla danego przekroju, p- ciśnienie w miejscu danego przekroju

10. Równanie Bernouliego dla cieczy rzeczywistej W przypadku cieczy rzeczywistej część energii, jaką struga przepływająca między dowolnie obranymi przekrojami jest zużywana na pokonanie oporów ruchu wywołanych głównie lepkością cieczy, szorstkością ścian przewodu itp. Aby równanie Bernoulli'ego i w tym przypadku mogło być słuszne, do prawej strony równania należy dodać pewną wysokość h_str obrazującą straty energetyczne (lub sumę tych start) zużyte na pokonanie wyżej wymienionych oporów. W związku z tym dla strugi cieczy rzeczywistej równanie Bernoulli'ego przyjmuje postać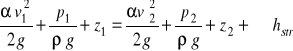
Współczynnik  ( ≥ 1) zwany współczynnikiem Saint-Venanta (lub Coriolisa) wyraża stosunek sumy energii kinetycznej strug elementarnych do energii kinetycznej całego strumienia

Tor cząsteczki (elementu płynu) - linia, którą zakreśla cząsteczka poruszając się w przestrzeni i w czasie

Linia prądu - wektory prędkości wszystkich cząsteczek położonych na linii prądu są w danej chwili do tej linii styczne. Linie prądu nie mogą się krzyżować.

Strugą cieczy - nazywamy zbiór linii prądu przechodzących prostopadle przez wszystkie punkty elementy pola dA. Linie prądu przechodzące przez kontur pola dA tworzą rurkę prądu.

Strumień cieczy jest pojęciem określającym wszystkie strugi cieczy przechodzące przez dowolnie wyodrębnioną powierzchni przekroju poprzecznego A cieczy, prostopadłą do wszystkich linii prądu.

Przekrój poprzeczny strugi, strumienia A - pole powierzchni prostopadłej do wektorów prędkości.

Wydatkiem (natężeniem przepływu) nazywamy objętość cieczy przechodzącej przez przekrój czynny w jednostce czasu.

Lepkość- Jest to własność płynu, dzięki której mogą pojawiać się w nim siły ścinające.

Współczynnik m - zależy od własności płynu. Jest nazywany dynamicznym współczynnikiem lepkości, albo w skrócie lepkością dynamiczną Stosunek lepkości dynamicznej μ do gęstości ρ nazywany jest lepkością kinematyczną

11. Przepływ wody przez próg - przepływ spokojny

12. Przepływ wody przez próg - przepływ rwący

Analiza zjawiska dotyczy układu zwierciadła cieczy na progu w zależności od jego położenia przed progiem i rodzaju ruchu w korycie. W rozważaniach przyjęto ustalone warunki przepływu (Q=const.) oraz pomijalnie małe ubytki energii na wejściu strumienia na próg. Oznaczając wysokość progu przez Δh oraz głębokość napełnienia w danym przekroju przez h równanie bilansu całkowitej wysokości energii strumienia ( E= h+αV^2/2g ) przed i nad progiem można zapisać E1=E2+Δh

Spokojny przepływ

-przy zbyt małym napełnieniu energia strumienia jest za mała, aby ciecz mogła przepłynąć przez próg. Wtej sytuacji nastąpi podniesienie zwierciadła cieczy w korycie do minimalnej głębokości wystarczającej do przepłynięcia cieczy

-spiętrzenie cieczy odpowiada krytycznemu przepływowi przed progiem, tzn minimalnej energii całkowitej E2

Rwący przepływ

-aby przeprowadzić ciecz ponad progiem, konieczne jest spiętrzenie strumienia

-dla małego napełnienia ciecz będzie przepływać ponad progiem z jednoczesnym podniesieniem się jej poziomu powyżej zwierciadła w korycie

13. Promień hydrauliczny i przekrój hydraulicznie najkorzystniejszy

Promien hydrauliczny jest obliczany jako stosunek powierzchni przekroju A do obwodu zwilżonego Oz koryta (stosunek pola przekroju zajętego przez przepływającą ciecz do obwodu zwilżonego)

Rh=A/Oz

Hydraulicznie najkorzystniejszy jest taki przekrój, przez który przy danych: spadku hydraulicznym i polu powierzchni przekroju, strumień objętości cieczy płynącej ruchem jednostajnym jest maksymalny.

14. Przepływ krytyczny i równanie energii

Przepływ krytyczny w korycie otwartym to przepływ, który odbywa się z taką głębokością, że energia właściwa strumienia jest minimalna E= h + αV^2 / 2g

---