Sprawozdanie z laboratorium elektroniki w Zakładzie Urządzeń Elektrycznych i Architektury Komputerowej

Temat: Badanie układów arytmetycznych. Sprawozdanie wykonała: Ewa Piotrowska Rok I, gr. II iz17/ I zespół

Data: Ocena: Podpis:

1. Celem ćwiczenia jest poznanie działania i możliwości wykorzystania sumatorów, komparatorów oraz jednostki arytmetyczno-logicznej ALU, a także poznanie zasad projektowania i budowy układów wykonujących operacje arytmetyczne, logiczne i arytmetyczno-logiczne.

2. Przeprowadzić badanie półsumatora realizującego sumę dwóch cyfr dwójkowych według następującej tablicy prawdy:

Wynikające z niej funkcje logiczne:

Schemat półsumatora:

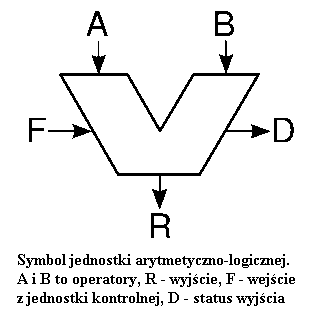
Jednostka arytmetyczno-logiczna (z ang. Arithmetic and Logical Unit, w skrócie ALU) to układ cyfrowy prowadząca proste operacje na liczbach całkowitych - działania arytmetyczne (takich jak dodawanie) oraz operacje logiczne (np. NAND) pomiędzy dwiema liczbami. Jest to podstawowy blok centralnej jednostki obliczeniowej komputera i jedna z głównych części procesora.

Typowe ALU ma dwa wejścia odpowiadające parze argumentów i jedno wyjście na wynik. Operacje jakie prowadzi to:

• operacje logiczne AND, OR, NOT, XOR

• dodawanie

• często też, odejmowanie, negacja liczby, dodawanie z przeniesieniem, zwiększanie/zmniejszanie o 1

• przesunięcia bitowe o stałą liczbę bitów, czasem też o zmienną liczbę

• dość często mnożenie i czasem dzielenie/modulo

Przyczyną dla której operacje te grupuje się w ALU jest to, że bramek logicznych potrzebnych do zaimplementowania wszystkich operacji z zestawu: dodawanie (z przeniesieniem i bez), odejmowanie (z przeniesieniem i bez), negacja liczby zwiększanie i zmniejszanie o 1, AND, OR, NOT, XOR jest niewiele trudniejsze od zaimplementowania samego dodawania. Mnożenie jest już droższe, a dzielenie jest bardzo drogie w porównaniu do tych operacji, dlatego pomimo że procesory o architekturze superskalarnej zawierają kilka ALU i mogą ich używać jednocześnie, to tak naprawdę podaczas kilku operacji dodawania (często niejawnych dla programisty, np. przy wyliczaniu adresu pola obiektu na podstawie adresu obiektu czy dostępu do n-tej zmiennej na stosie) wykonują tylko jedno mnożenie.

3. Przeprowadzić badanie sumatora pełnego wykonującego dodawanie trzech bitów wejściowych według następującej tablicy prawdy:

Realizowane funkcje:

4. Przeprowadzić badanie scalonego 4-bitowego sumatora dwójkowego UCY 7483, dodającego do siebie dwie liczby czterobitowe i wykorzystującego poprzednie przeniesienie C₀ oraz wytwarzającego przeniesienie z aktualnej operacji C₁

5. Przeprowadzić badanie 4-bitowego komparatora dwójkowego UCY 7485, porównującego dwie liczby 4-bitowe i sygnalizującego określony warunek (A=B, A>B, A<B) odpowiednim stanem wysokim na wyjściach 5, 6 lub 7. Wejście 2, 3 i 4 służą do łączenia komparatorów, czyli tworzenia układów służących do porównywania liczb o większej liczbie bitów.