Połączenia, w których V~jstępują wiązania koordynacyjne noszą nazwę związków koordynacyjnych, związków komplekso'"'"Jch, albo kompleksów.

W związku kompleksowym wyróżnia się atom centralny i cząsteczki koordynowane zwane ligandami.

Wiązania wodorowe. lest to słabe oddziaływanie elektrostatyczne pomiędzy elektroujemnym atomem (akceptorem), a atomem wodoru, który jest kowalencyjnie połączony z innym atomem elektroujemnym (donorem). W wiązaniu tym wodór pełni rolę mostka łączącego dwa elektroujemne atomy.

1. 

2. 

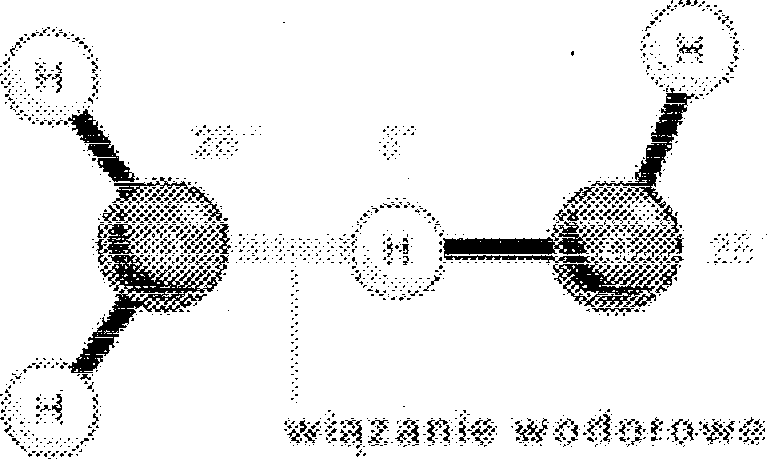
:"'~"""',>;>;/'"""~~""""""''''''''''''''''''''"''''''''''"''.r.-.-.-.-.-.-_-_ ••.••••• -.;

• .

• .

• .

• .

()

Siły van der Waalsa

są bardzo słabymi oddziaływaniami zachodzącymi pomiędzy wszystkimi typami atomów (zarówno polarnymi jak i niepolarnymi). W chmurze elektronowej otaczającej jądro pojawiać się mogą chwilowe fluktuacje rozmieszczenia ładunków ujemnych - wynik normalnego ruchu elektronów. Takie nieregularności prowadzą do po"\vstawania i zanikania dipoli, które wpływają na rozmieszczenie elektronó\v "V sąsiednich atomach.

Gdy atomy znajdujące się w bezpośrednim sąsiedznvie mają spolaryzowane chmury elektronowe, poja\viać się może słabe przyciąganie. Zanika ono bardzo szybko wraz ze wzrostem odległości między atomami, natomiast gdy atom)' znajdą się zbyt blisko siebie zostają odepchnięte przez jednoilnicl1ne -ładurJ<:i chmur elektronovv~fch.

Oddziaływania van der Waalsa odpowiadają na przykład za przyciąganie się cząsteczek niepolarnych cieczy oraz stanowią siły łączące składniki ścian komórkowych (poprzez przycia.ganie się niepolarnych łańcuchów fosfo lipidów).

8. Prawo działania mas Guldberga i \Vaagego.

Stała równowagi - prawo działania mas Guldberga i Waagego

nA +mB = qC + rD

Substancje reagują tak dł-Jgo, dopóki stosunek iloczynu stężeń produktów do iloczynu stężeń substratów pje osiągnie pewnej

stałej waltości, charaktetystycznej dla danej reakcji i dla temperatury

5

Reakcje odwracalne

CO + H₂0=C0₂ + H₂ +9.64 kcal

₁

hl rn -1-1 h' H 0-1 ..... h; ro .•.... b· H

oVJ' ~~, OvJ. 2 - ~ ~VJ' ~ 2 + l ~ J. 2

CO₂ +H₂ =CO+H₂0 -9.64 kcal

rn+H o~r'n -I-H

-.........., 2""-"" '-"'J 2 l 2

Wszystkie reakcje chemiczne p..aieży uznać za odwracalne, lecz stopień

"~""b' •. '" kL';· "'d-n.,.,. +....".0;; t dl r" ..;,....",TL'1>h •• k;; r" .

PU .. ", 1egu .",a "'J1 V VHO~H"'J Jes a .OL.HY"" .ea CJ' .oz.~y.

Jeżeli przebieg reakcji odwrotnej tmdno jest stwierdzić, to przyjmuje się, że dana reakcja jest nieodwracalna, czyli że przebiega praktycznie jednokierunkowo.

Reakcje nieodwracalne

Fe+CuS0₄ ~FeS04 +Cu

Położenie ró\vnowagi chemicznej zależy nie tylko od rodzaju reakcji chemicznej, lecz takie od stężeń składników reagujących.

9. Prawo Daltona.

p = pl + p2 + .

_C

' [.nl· enl' e wywt'erane '"'rz""z tn;""""'ant'nę gazo' '" n;e rea^m1;ą",,,,,,h .,."" s,.,.hg ;""st ro'wne s"m;"" "';[."';""n' J"akt"e

. ~ ... ł' .•..... l,LU .•.•••• ""'L< _.I, l \''1 u.' ó-J ,",)"',U. L..l'" -VV\.ŁJ •.••••. _ u .U'i",I ....,l~~U •.••.• l a:

wywierałby każdy z gazów wchodzących w skład mieszaniny, gdyby sam został umieszczony w całej objętości zajmowanej przez mieszaninę.

Równanie stanu gazu doskonałego:

p·V=n·R·T p=c·R·T

q r

K = Pc 'PD

c r:-

_P

mRTI

A 'PB .. t'

H₂ + J₂ <=> 2IU

W stanie równowagi dynamicznej: nHJ = nH2 + J2

V,.TT = k] . c_H2 • c_J2

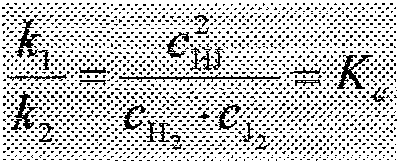
6

II.Stała i stopień dysocjacji.

Dysocjacja elektrolityczna - samorzutny rozpad cząsteczek na jony pod wpływem rozpuszczalnika (woda, ciekły amoniak)

Stopień dysocjacji

liczba cząstek zdysocjm.vanych n

_a

- --

- - .

pierwotna liczba cząstek no

a. = l - elektrolity mocne Stała dysocjacji

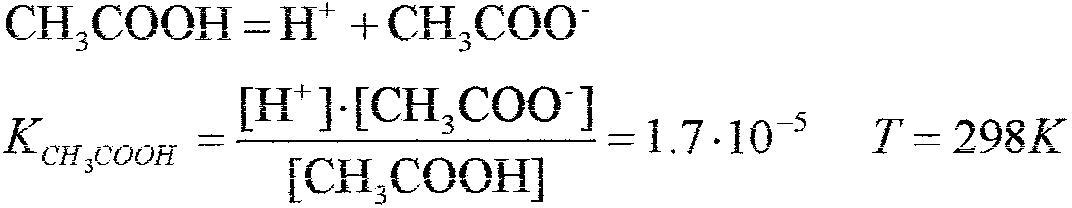
Położenie równowagi chemicznej zależy nie tylko od rodzaju reakcji chemicznej, lecz także od stężeń składników reagujących

Przykład:

Mieszanina kwasu solnego i kwasu octowego o stężeniach, koiejno 0.05 i 0.1 mol/dm3

Hel ~H+ +CI-

[H+]·[COOH-] KCHpJOH = [CH₃COOH]

K , -c- = [H+}-[CH₃COO-] -l 7.10-⁵ = (0,05 +x)- x

CHl·ouJt [CH₃COOH]' (0,1- x)

W formie uproszczonej:

_ 1,7.10-⁵ -0,1:::: 0,000034 mol/dm ³ x- 005

,

7

Dla poró\vnania liczba moli zdysocjowanego samego kwasu octO\vego wynOSI:

~ - - [5 . 1Jd 3

\V l.Ofillle uproszczonej: x = v¹,7 ·10- - 0,1 = 0,0013 mo 111

Przykład zależności stałej dysocjacji od stopnia dysocjacii:

[H+]-[CH₃COO-] KCH3COOH = [CH₃COOH]

[H+]-[CH₃COO-] _ x² KCH3COOH = [CH "OOPl - (c- - x)

'~3'-"/ ~LJ U

12.I1oczyn rozpuszczalności. vi

_A

U-A+ I u- K _[A+]-[R]

•. ~- T~ "-AE- r 1

tABlSL

~. rozpuszczalności jest to wartość ilocZ'jnu jonowego całkowicie zdysocjowanego elektrolitu. będącego w równowadze z formą niezdysocjowaną. i

A B =nA+^m +mB-ⁿ

n m - -

~wiązek	iŁ
IAgCl	10-10
AgBr	2 -W-B
AgI	2,5 "10-16
iCaS04	22-10-4
	, -
A..gS2	5,6 -lO-51

8

Przykład

Jak ""płynie O, l molo",,)' roztwór kwasu solnego na liczbę jonów srebra obecnych w roztworze w stanie równowagi.

_L

-10-10 ----- [A +]-10-5 lld 3

AgCI - --? ~ g-\.. mo. m

T -ln-^lO - (O l-1--v'l. d ;",v-rAo+l-rrl<-J

.LJAgC/-J-V ~_., ,.L ł .<:t.J X, g Z.i."" .... ~-l.J...1b J-l"-.../

10-10

[Ag+]=-'-= 10-⁹ mol/dm³ 0,1

13. Wpływ Hel na stopień dysocjacji kwasu octowego.

14.'Vpływ HCI na rozpuszczalność chlorku srebra.

15. Iloczyn jonowy wody, pH.

iloczyn jonowy wody - iloczyn stężenia jonów wodorowych i wodorotlenkowych w wodzie i roztworach wodnych, powstaje w wyniku autodysocjacji wody; wielkość stała w danej temperaturze,

_d

L "'50C ' - . '1*10 -14 1/1._3 la L, rowny JeSt· mo om .

cli - ujemny dziesiętny logarytm stężenia jonów wodorowych w roztworze; wielkość określająca odczyn roztworu; dla roztworów wodnych moie przybierać wartości od O do 14.

pH = -lOglO[H₃0+]

16.Zjawisko dyfuzji, I prawo Ficka.

Dyfuzja - proces rozprzestrzeniania się cząsteczek w gazie, cieczy lub ciałach stałych pod wpły-wem różnicy ciśnień parcjalnych. Dyfuzja prowadzi do wyrównania się stężeń. Osiągnięcie stanu równowagi nie oznacza jednak ustania dyfuzji. Trwa ona nadaL jednak dzięki dokładnemu wymieszaniu się wszystkich składników, nie prowadzi już do zmian stężenia.

I prawo Ficka:

oh = -D! x dc/dx 1. = 1/" 'V Am Id t

.::!.J .l. u h UJ, H'·

oh - przepłYVl masy składnika i, D_i - współczynnik dyfuzji,

dei - zmiana stężenia ci wzdłuż osi x, S -pole powierzchni.

dm/dt =:11 x S x dęidx

Ilość substancji dyfundującej w czasie t przez określoną powierzchnię prostopadłą do kierunku dyfuzji, jest proporcjonalne do pola powierzchni S, gradientu stężeń

1 czasu.

9

_W

'I ok d fi" ł d ~ o o D . lk " . ha k . d fi .. [m2/ l

SpO czynm. y.nZ]l, sta a YlnZJI, ,WIe •• osc c ra ~teryzująca y UZJę, ma wymiar CL ,8_j,

zależy od temperatury i ciśnienia. "Współczynnik dyfuzji równy jest liczbowo ilości składnika dyfundującego przez jednostkową powierzchnię w jednostce czasu, przy jednostkowym gradiencie stężenia powodującym dyfuzję.

3. 

17.Dyfuzja stężeniowa.

c

Bez

• o

nlleszanla

Rozkład stężeń substancji podczas separacji ciśnieniowej

c

p

10

18.Równowaga Donnana.	I
R-		er
ej		C2
Na+		-I-
	I	ł~a'

R-		-	+
Cj +X	C^1-		-ł-	er
	~ .	-
			I
Na+		-	+	Na+	C2-^X
			+

x(cl+x) = (c2-x)(c2-x)

19. Wymiana jonowa.

Wymiana jonowwto zjawisko i proces wymiany mchlivy'Jch jonów na inne jony tego samego znaku zachoa';ący na ciele stałym lub polimerze zawierającym odpowiednie grupy funkcyjn$'o

Procesy dyfhzyjne podczas wymiany jonowej

Ci

Nąjwolniejsze etapy dyfuzji:

4. 

et

roztwór

jonit

w fazie jonitu

w warstwie adhezyjnej

",,- warstwa adhezyjna