Dane:
n=5
i=5
P1= 10 [kN]
P2= 10 [kN]
P3= 5 [kN]
P4= 5[kN]
P5= 10[kN]
E=2,1e5[MPa]
1. Wyznaczenie reakcji w utwierdzeniu (RA):
∑ Fix= RA-P5+P4-P3+P2-P1=0
RA= P5+-P4+P3-P2+P1
RA= 10[kN]-5[kN]+5[kN]-10[kN]+10[kN]
RA= 10[kN]
2. Wyznaczenie sił w poszczególnych fragmentach pręta:
N1=P1
N1=10[kN]
N2=P1-P2
N2=0[kN]
N3=N2=0[kN]
N4=P3+P1-P2
N4=5+10-10 [kN]=5[kN]
N5=N4=5[kN]
N6=P1-P2+P3-P4
N6=10-10+5-5[kN]= 0[kN]
N7=N6=0[kN]
N8=P1-P2+P3-P4+P5-RA
N8=10+-10+5-5+10-10[kN]=0[kN]
a= 125 [mm]
b= 100 [mm]
c= 80 [mm]
d= 100 [mm]
e= 100 [mm]
f= 62,5 [mm]
g= 200 [mm]
h= 100 [mm]
3. Obliczenie naprężeń:
Wzór:
∂=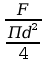
Po wstawieniu odpowiednich danych do wzoru otrzymujemy:
∂1=1,27[MPa]
d1=100[mm]
F=N1=10[kN]
∂2=0[MPa]
d1= 100[mm]
F=N2=0[kN]
∂3=0[MPa]
D2=200[mm]
F=N3=N2=0[MPa]
∂4=0,16[Mpa]
D2=200[mm]
F=N4=5[kN]
∂5=0,28[MPa]
D3=150[mm]
F=N5=N4=5[kN]
∂6=0[MPa]
D3=150[mm]
F=N6=0[kN]
∂7=0[MPa]
D4=200[mm]
F=N7=N6=0[kN]
∂8=0[MPa]
D4=200[mm]
F=N8=0[kN]
4. Dobranie średnicy pręta:
∂dop=125[MPa]
Warunek:
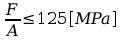
Gdzie:
A=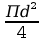
F=10[kN] (największa z sił występujących w pręcie)
Przekształcenie nierówności:
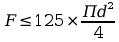 (1)
(1)
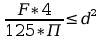 (2)
(2)
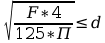 (3)
(3)
Jednostki:

Skoro
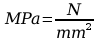
Więc
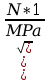
Po wstawieniu danych do wzoru otrzymujemy:
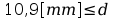
Odp.: dla naprężenia dopuszczalnego równego 125 [MPa] średnica pręta powinna bć większa bądź równa 10,9[mm].
5.Obliczenie wydłużeń na poszczególnych odcinkach pręta:
Wzór:
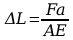
Gdzie:
E=2,1e5[MPa]
Jednostki:
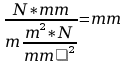
ΔL1=0,6*10-3 [mm]
d1=100[mm]
F=N1=10[kN]
a=100[mm]
ΔL2=0[mm]
d1= 100[mm]
F=N2=0[kN]
a=200[mm]
ΔL3=0[mm]
d2=200[mm]
F=N3=N2=0[MPa]
a=62,5[mm]
ΔL4=0,08*10-3[mm]
d2=200[mm]
F=N4=5[kN]
a=100[mm]
ΔL5=0,08[mm]
d3=150[mm]
F=N5=N4=5[kN]
a=100[mm]
ΔL6=0[mm]
d3=150[mm]
F=N6=0[kN]
a=80[mm]
ΔL7=0[mm]
d4=200[mm]
F=N7=N6=0[kN]
a=100[mm]
ΔL8=0[mm]
d4=200[mm]
F=N8=0[kN]
a=125[mm]
5. Wartość wydłużenia całkowitego:
ΔLcałkowite= ΔL1+ΔL2+ΔL3+ΔL4+ΔL5+ΔL6+ΔL7+ΔL8
ΔLcałkowite= 0,6*10-3+0+0+0,08*10-3+0,08+0+0+0[mm]
ΔLcałkowite=0,081[mm]
Wyszukiwarka