Zestaw XVI

Zad 1

a₂=-1/ a₁=-1/2 z pkt przecięcia osi y wynika że b=-3 zatem: y=-1/2 x-3 to szukany wzór prostej

Zad 2

Równanie ogólne okręgu: (x-a)²+(y-b)²=r² S=(a,b) ---> współrzedne środka S=(1,3)

Z punktu P=(-2,-1) mamy: x=-2 y=-1 postawiamy do równania dane z zadania i mamy: (-2-1)²+(-1-3)²=r²

9+16=r² 25=r² Równanie okręgu ma postać: (x-1)²+(y-3)²=5²

Zad 3

znajdujemy współrzędne środka odcinka AB, oznaczmy ten punkt jako S xs=(-1+3)/2=1 ys=(3+7)/2=5

Zatem S=(1,5) znajdujemy teraz równanie prostej przechodzącej przez punkty S i P podstawiając odpowiednie współrzędne tych punktów do równania prostej w postaci y=ax+b P=(0,8)

8=a*0+b, z tąd b=8 S=(1,5) 5=a*1+b 5=a+8 a=-3 zatem szukana prosta ma postać y=-3x+8

Zad 4

y= 5-x y = 5-4 y=1 -3 =5-x x = 8

Zad 5

(x-3)²+(y-5)²=4 x + y = 10 ---> x =10 –y (10-y -3)^2 + y^2 -10y +25 = 4 (7-y)^2 + y^2 -10y +25 = 4

49 -14y +y^2 +y^2 -10y +25 = 4 2y² -24y + 70 =0 Y² -12y +35 = 0 Δ = 144 -4*35 = 144 -140 = 4

√Δ = 2 y1 =( 12 -2)/2 =5 y2 =(12 +2)/2 =7 x1 =10 -y1 = 10 -5 = 5 x2 =10 -y2 = 10 -7 = 3

Odp. A =(5,5) B = (3,7)

Zad 6

A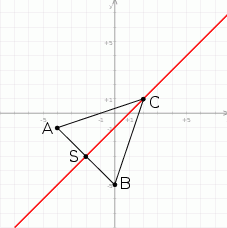 C=√40

BC=√40

AB=√32

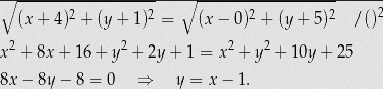
Zad 7

równanie AB: y=ax+b -2=-8a+b -2=4a+b b=8a-2 -2=4a+8a-2 -2+2=12a

a=12:0=0 b=8×0-2 b=-2 równanie AB: y=-2[ to prosta równoległa do osi X]

równanie AC: y=ax+b 3=-8a+b -2=-8a+b

równanie sprzeczne, bo dla tej samej wartości x, równej -8, przyporządkowane są

różne wartości y: raz -2, drugi raz 3, więc nie istnieje równanie prostej,

jest to prosta równoległa do osi Y, i przechodząca przez

x=-8 czyli to trójkąt prostokątny równanie prostej BC: y=ax+b 3=-8a+b -2=4a+b

b=8a+3 -2=4a+8a+3 12a=-2-3 a=-5/12 b=8×-5/12+3=-40/12+86/12=-⅓

równanie BC:y=-5/12x-⅓

b]

obliczam długość AB=√[(4+8)²+(-2+2)²]=√144=12

obliczam długość AC=√[(-8+8)²+(-2-3)²]=√25=5 BC=√[AC²+AB²]=√5²+12²=√[25+144]=√169=13

AC+AB> BC 5+12>13 17>13

C]

R OKREGU OPISANEGO = ½C=½×13=6,5

Zad 8

Wyznaczmy prostą SP podstawiając pod (x,y) współrzędne punktów: y=ax+b

S(-2,3), P(2,7): 3=-2a+b 7=2a+b

dodajemy stronami i mamy: 10=2b |:2 b=5

wstawiamy: 7=2a+b 7=2a+5 2a=2 |:2 a=1

tak o to nasza prosta y=ax+b ma równanie: y=x+5

prosta przecina okrąg w dwóch miejscach i je musimy wyznaczyć, a z rysunku odczytamy, które miejsce jest tym poprawnym... liczymy punkty przecięcia:

(x+2)²+(y-3)²=8

y=x+5

podstawiamy pod y w pierwszym równaniu "x+5":

(x+2)²+(x+5-3)²=8 (x+2)²+(x+2)²=8 2(x+2)²=8 |:2 (x+2)²=4 x²+4x+4=4 x²+4x=0

wyłączamy "x" przed nawias: x(x+4)=0

widzimy, że równanie jest prawdziwe dla x=0 oraz dla x=-4 (co się zgadza idealnie z rysunkiem). To też na rysunku widzimy, że obchodzi nas x=0... trzeba aby y wyliczyć, ale to proste, skoro:

y=x+5 y=5

tak więc nasz punkt A ma współrzędne (0,5)

Zad 9

prosta k: y = 2x +1 prosta l:y = x + 3 ich wspólny pkt. Przecięcia 2x+1=x+3 stąd x=2 i y=5

wsp. pkt. A (2 ; 5) równanie prostej m prostopadłej do k więc jej wsp. kierunkowy równy -0,5

m: y = -0,5x+b podstawiamy wsp. pkt.C 1=-0,5*4+b stąd b=3 równanie prostej m:y=-0,5x+3

pkt. B przecięcia prostej m i l x + 3 = -0,5x + 3 stąd x = 0 oraz y = 3 wsp. pkt. B (0;3)

pole trójkąta ABC A (2 ; 5) B (0 ; 3) C (4 ; 1) P = 0,5 | (Xb - Xa)(Yc-Ya) - (Yb-Ya)(Xc-Xa) |

P = 0,5 | (0 - 2)(1-5) - (3-5)(4-2) | = 12

Zad 10

a) Punkt A należy do wykresy gdy dla x = -5 f(x) = 7, zatem:

7 = (2 - a)*(-5) + 3 7 = -10+5a +3 7=5a-7

5a = 14 a = 14/5 = 2,8

b) funkcja jest rosnąca gdy współczynnik "a" (zakładając ogólny wzór funkcji liniowej y = ax + b) jest większy od zera, więc: 2 - a > 0 /-2 -a > -2 /*(-1) a < 2

c) obliczamy dla jakiego x wartość funkcji wyniesie 0 (jest to punkt przecięcia się wykresu z osią OX) -0,75x + 6 = 0 -0,75x = -6 /* (-1) 0,75x = 6 /:0,75 x=8

podstawiamy do funkcji f(x) 0=(2-a)*8+3 0=16-8a+3 8a=19 a=19/8=2,375

Zad 11

A = (6, 1) B = (-2, 5) C = (-6, -1) x²+y²-2ax-2by+c=0 A=(6;1)

x²+y²-2ax-2by+c=0 6²+1²-2a*6-2b*1+c=0 36+1-12a-2b+c=0 37-12a-2b+c=0

B=(-2;5) x²+y²-2ax-2by+c=0 (-2)²+5²-2a*(-2)-2b*5+c=0 4+25+4a-10b+c=0 29+4a-10b+c=0

C=(-6;-1) x²+y²-2ax-2by+c=0 (-6)²+(-1)²-2a*(-6)-2b*(-1)+c=0 36+1+12a+2b+c=0

37+12a+2b+c=0 37-12a-2b+c=0 29+4a-10b+c=0 37+12a+2b+c=0 c=12a+2b-37

29+4a-10b+12a+2b-37=0 37+12a+2b+12a+2b-37=0 16a-8b-8=0 24a+4b=0

16a-8b-8=0 4b=-24a /:4 16a-8b-8=0 b=-6a 16a-8(-6a)-8=0 b=-6a 16a+48a-8=0 64a=8 /:64 a=8/64 a=1/8 b=-6a b=-6*1/8 b=-6/8 b=-3/4 S=(a;b) S=(1/8 ; -3/4)