m10

#K$Sieć Hopfielda

Sieci Hopfielda są najczęściej stosowaną podklasą sieci neuronowych wykorzystywanych w praktyce. Zostały one zdefiniowane w historycznej pracy tego badacza, której publikacja w 1982 roku stała się punktem zwrotnym w badaniach sieci neuronowych i przywróciła zainteresowanie tymi systemami sferze dociekań naukowych. Sieci te charakteryzują się występowaniem sprzężeń zwrotnych. Wszystkie połączenia, które w tej sieci występują są sprzężeniami zwrotnymi, wszystkie sygnały wyjściowe są wykorzystywane jako wejścia i wszystkie wejścia do wszystkich neuronów przenoszą sygnały sprzężenia zwrotnego. W sieciach tych neurony mają nieliniowe charakterystyki:

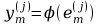
gdzie

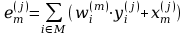
a nieliniowość 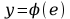dana jest prostą binarną funkcją

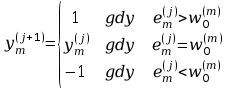
Warto przy tym zwrócić uwagę na dwa szczegóły podanych wyżej wzorów. Otóż po pierwsze, współczynniki wagowe 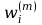łączące wyjście i-tego neuronu z wejściem m-tego neuronu nie zależą od j. Wynika to z faktu, że rozważając sieć Hopfielda na tym etapie nie dyskutujemy jej uczenia. Zakładamy, że wartości 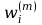zostały wcześniej ustalone za pomocą jakiegoś algorytmu ( najczęściej przyjmuje się tu algorytm Hebba) i obecnie nie podlegają zmianom. Numer j oznacza natomiast chwilę czasową, określającą w jakim momencie procesu dynamicznego następującego pop pobudzeniu sieci obecnie się znajdujemy. Zagadnienie to będzie niżej dokładnie dyskutowane. Po drugie sumowanie sygnałów wyjściowych 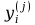z poszczególnych neuronów w wzorze definiującym łączne pobudzenie 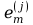odbywa się po wszystkich elementach 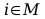czyli po wszystkich elementach sieci. Oznacza to, że w sieci przewidziane są także połączenia z warstw dalej położonych (wyjściowych) do warstw wcześniejszych - czyli sprzężenie zwrotne.

Jak było to wcześniej odnotowane, sieć o takim schemacie połączeń nazywana jest siecią autoasocjacyjną. W ramach tego sprzężenia każdy neuron jest także połączony jednym z wejść ze swoim własnym wyjściem, zatem zasada autoasocjacyjności odnosi się także do pojedynczych neuronów. Każdy neuron sieci ma także kontakt z pewnym, odpowiadającym mu sygnałem wejściowym 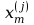, zatem zaciera się tu podział na warstwę wejściową i pozostałe warstwy sieci.

Procesy zachodzące w sieciach Hopfielda są zawsze stabilne. Stabilność procesów w sieci Hopfielda osiągnięto dzięki:

Z siecią Hopfielda kojarzy się tzw. “funkcje energii” (nazwa ta ma charakter czysto umowny – nie jest związana z rzeczywistą energią), zwaną też funkcją Lapunowa. Funkcja ta opisuje zbiór stanów sieci Hopfielda, zdefiniowanych przez zbiór wartości wyjść elementów przetwarzających tejże sieci. Można udowodnić, ze funkcja taka, dla sieci Hopfielda w skończonej ilości kroków osiągnie swoje minimum lokalne oraz że jest to funkcja nierosnąca w czasie – co jest równoznaczne ze stwierdzeniem, że procesy zachodzące w sieci Hopfielda są procesami stabilnymi.

Łatwość budowy i stosowania sieci Hopfielda powoduje, że są one bardzo popularne. Znajdują one liczne zastosowania - między innymi przy rozwiązywaniu zadań optymalizacji, a także przy generacji określonych sekwencji sygnałów, następujących po sobie w pewnej kolejności. Pozwala to za pomocą takich sieci tworzyć i wysyłać do różnych obiektów sygnały sterujące. Sieci Hopfielda mogą także pracować jako tzw. pamięci autoasocjacyjne.

Koncepcja pamięci autoasocjacyjnej wiąże się z jedną z podstawowych funkcji mózgu – z odtwarzaniem całości informacji na podstawie informacji niepełnej. Jest to zdolność sieci do prawidłowego zinterpretowania danych zniekształconych lub niekompletnych. Sieć pracująca jako pamięć autoasocjacyjna może także usuwać zakłócenia i zniekształcenia różnych sygnałów - także wtedy, gdy stopień “zaszumienia” sygnału wejściowego wyklucza praktyczne użycie jakichkolwiek innych metod filtracji.


struktury danych algorytmu:

Wagi – wektor wag neuronów w sieci

Wzorzec – wektor wzorców rozpoznawanych przez sieć

rozM - rozmiar sieci - poziomo (domyślnie 25)

rozN rozmiar sieci - pionowo (domyślnie 25)

nMax – ilość neuronów w sieci

Użyta w programie procedura TabNaWzorzec przepisuje do wzorca wartość elementy tymczasowego, procedura WzorzecNaTab działa dokładnie odwrotnie.


for k := 1 to 16 do

if tZrB[k] then begin

Inc(nElem);

if nrWzorca = k then nrWz := nElem;

TabNaWzorzec(tZr[k],Wzorzec[nElem]);

end;


if nrWz = 0 then

Exit;


( ustawinie wag sieci }

for k := 1 to nMax do begin

for i := 1 to k-1 do begin

Wagi[k,i] := 0;

for j := 1 to nElem do

Wagi[k,i] := Wagi[k,i] + (Wzorzec[j,k]*Wzorzec[j,i]);

Wagi[i,k] := Wagi[k,i];

end;

end;


Randomize;

{ przpisanie wzorca 1 do wzorca 2 i wprowadzenie zmian dla wzorca 2}

for i := 0 to 25 do

for j := 0 to 25 do

tOdp[2,i,j] := tOdp[1,i,j];

for i := 1 to Trunc(enZmPkt.Value) do begin

j := Trunc(rozM*Random);

k := Trunc(rozN*Random);

tOdp[2,j,k] := 1 - tOdp[2,j,k];

end;


{przerysowanie ekranu}

.....


{ przepisanie zmienionego wzorca do obszaru roboczego }

TabNaWzorzec(tOdp[2],Wzorzec[21]);

TabNaWzorzec(tOdp[2],Wzorzec[22]);


Licz1 := 0; Licz2 := 0;

{ rozpoznawanie }

repeat

for i := 1 to nMax do

Wyj[i] := Wzorzec[21,i];


{ oblicznie odpowiedzi sieci }

for i := 1 to nMax do begin

wy := 0;

for j := 1 to nMax do

if i <> j then

wy := wy + (Wyj[j]*Wagi[j,i]);


if wy > 0 then

Wyj2[i] := 1;


if wy < 0 then

Wyj2[i] := -1;


if wy = 0 then

Wyj2[i] := Wyj[i];

end;


{ oblicznie różnic i ustawienie liczników }

rozn1 := 0; rozn2 := 0;

for i := 1 to nMax do begin

if Wyj2[i] <> Wzorzec[22,i] then

Inc(rozn2);

Wzorzec[22,i] := Wyj[i];

Wzorzec[23,i] := -1;

if Wyj2[i] <> Wyj[i] then begin

Inc(rozn1);

Wzorzec[23,i] := 1;

end;

Wyj[i] := Wyj2[i];

Wzorzec[21,i] := Wyj[i];

end;

if rozn1 = 0 then Inc(Licz1);

if rozn2 = 0 then Inc(Licz2);


{ rysuneki i opisy kroku rozpoznania }

if (Licz1 < 2) and (Licz2 < 3) then begin

Inc(iKrok);

WzorzecNaTab(Wzorzec[21],tOdp[iKrok]);

WzorzecNaTab(Wzorzec[23],tRoz[iKrok-2]);

{wyrysowanie kroku rozpoznawania na ekranie}

end;

until (Licz1 = 2) or (Licz2 = 3) or (iKrok = 49);


Opis modułu aplikacji

Pamięcią asocjacyjną nazywamy zdolność sieci do prawidłowego zinterpretowania danych zniekształconych lub niekompletnych. Sieć taka może także usuwać zakłócenia i zniekształcenia różnych sygnałów - także wtedy, gdy stopień “zaszumienia” sygnału wejściowego wyklucza praktyczne użycie jakichkolwiek innych metod filtracji

Moduł prezentuje model sieci Hopfielda pracującej jako pamięć autasocjacyjna.

Zadaniem będzie zapamiętywanie i odtwarzanie prostych obrazów.

Sieć potrafi odtworzyć pierwotny wzorzec na podstawie sygnału silnie zniekształconego lub zakłóconego, działa więc jako pamięć asocjacyjna. Użytkownik podaje sieci ciąg wzorców, a następnie wygenerowany sygnał zbliżony do jednego z tych wzorców.

Zadaniem sieci jest rozpoznanie wybranego wzorca (“podobnego” do sygnału na wejściu).

Poniżej prezentujemy ekran początkowy programu – przed wprowadzeniem wzorców przez użytkownika.

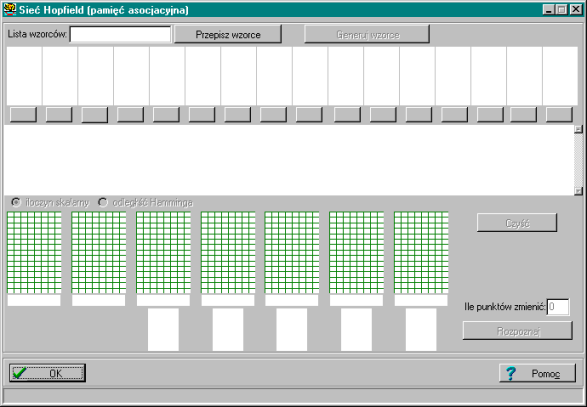
Pierwszym krokiem użytkownika przy pracy z programem jest określenie wzorców, które program ma rozpoznawać.

Ciąg wzorców może być generowany przez użytkownika automatycznie lub manualnie.

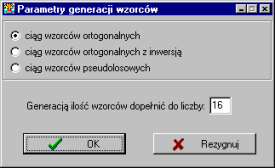
Przy generacji automatycznej użytkownik ma możliwość określenia czy chce generować ciąg wzorców (przycisk “Generuj wzorce” w górnej części okna programu).


Przy manualnej generacji (klikając na “Numer wzorca” użytkownik ma możliwość wejść do okna edycji wzorca) wzorca użytkownik określa, które punkty w matrycy wzorca są zapalone, a które “wygaszone”. Istnieje też możliwość przepisania znaku z klawiatury bezpośrednio do matrycy - należy w tym celu wprowadzić znak do pola edycyjnego i nacisnąć przycisk “Przepisz”.


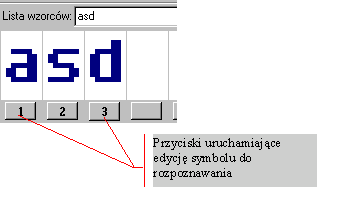
Poniżej prezentujemy zrzut okna edycji wzorca.


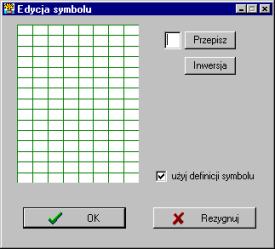
Za pomocą przycisku “Inwersja” użytkownik ma możliwość wygenerowania wzorca “odwrotnego” od poprzednio wprowadzonego. Check-box “Użyj definicji symbolu” określa czy dany wzorzec jest wykorzystywany przez sieć, czy tez nie.

Dodatkowo użytkownik programu ma możliwość edycji i wprowadzenia zmian na dowolnym ze wzorców (przycisk “Numer wzorca” pod wzorcem) oraz przepisania ciągu wzorców z łańcuchu znaków (przycisk “Przepisz wzorce” w górnej części okna programu ).

Po zbudowaniu ciągu wzorców użytkownik wybiera jeden z nich (klikając dwukrotnie na tym wzorcu) i zaburza go w określonej przez siebie liczbie punktów.

Proces rozpoznawania uruchamiany jest za pomocą przycisku “Rozpoznaj”. Kolejne kroki procesu rozpoznawania obrazu są przedstawiane w matrycach w dolnej części okna programu.

W edytorze w centralnej części ekranu wyświetlane są parametry rozpoznawania – iloczyn skalarny oraz odległość Hamminga (ilość punktów w których sygnały się różnią) pomiędzy zaburzonym wzorcem, a kolejnym krokiem rozpoznawania wzorca.

Poniżej prezentujemy zrzut ekranu, na którym sieć w sposób prawidłowy rozpoznała zaburzony wzorzec.

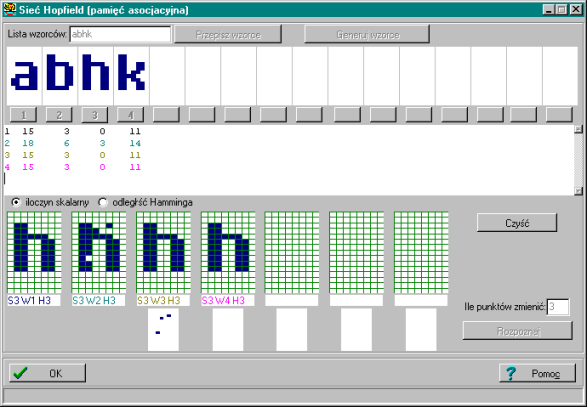
Sieć może nie być w stanie rozpoznać wzorca w sposób prawidłowy.

Wiąże się to z tzw. efektem “przesłuchów” występującym gdy podane wzorce są do siebie podobne. Przy podobnych wzorcach ślady pamięciowe bardziej nakładają się na siebie. Jeśli jednak są bardzo podobne, to ich zapisy w postaci składników wag poszczególnych neuronów tak bardzo mieszają się, że w gotowej sieci zaczyna być problematyczne prawidłowe odtworzenie któregokolwiek z zapamiętanych obrazów

Dlatego uzasadnione i sensowne jest korzystanie z ciągu wzorców różniących się od siebie w stopniu jak największym. Taką właśnie rolę spełnia generacja ciągu wzorców ortogonalnych – dla takich wzorców sieć wykazuje mniejszą “wrażliwość na podobieństwo wzorców”.

Poniżej zrzut ekranu z sytuacji, gdy rozpoznanie nie zakończyło się powodzeniem

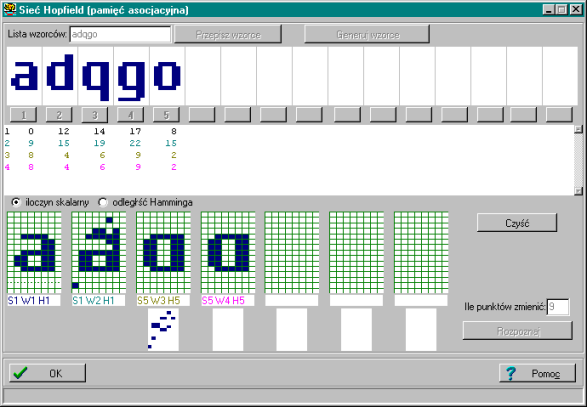
Zjawisko odtwarzania poprawnych obrazów z bardzo mocno zakłóconych wzorców w sieci Hopfilelda zapamiętującej ortogonalne sygnały też ma swoje granice. Jeśli zostanie zniekształcony zbyt mocno - nastąpi bezpowrotna utrata możliwości jego odtworzenia.


Poniżej – prawidłowe rozpoznanie wzorca zakłóconego w 14 punktach – dla wzorców ortogonalnych.

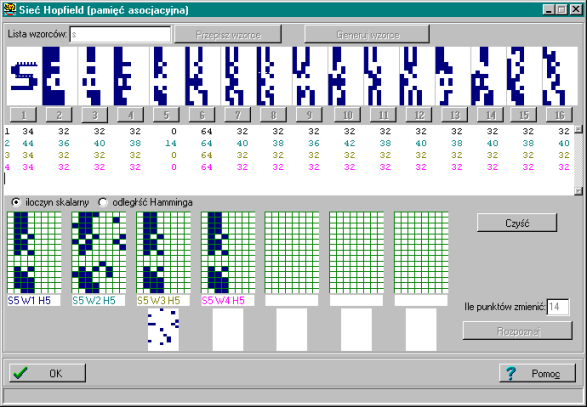
Powyższy moduł prezentuje najistotniejsze cechy sieci Hopfielda pracującej jako pamięć autoasocjacyjna.


# C_M10

K sieć ze sprzężeniem zwrotnym, sieć Hopfielda

$ Sieć Hopfielda


Wyszukiwarka