|
Zesp贸艂 8 |
In偶ynieria Ruchu Morskiego, rok I, gr. A |
|
|
|
膯wiczenie nr 3 Wyznaczanie temperatury Curie ferrytu
|
|
|
Data wykonania: 22.10.1997 |
Ocena: |
Podpis: |
TEORIA:
Polem magnetycznym nazywamy taki stan przestrzeni, w kt贸rym na poruszaj膮ce si臋 艂adunki dzia艂aj膮 si艂y. Jest ono wytwarzane przez poruszaj膮ce si臋 艂adunki pozostaj膮ce w ruch uporz膮dkowanym.
Podstawow膮
wielko艣ci膮 charakteryzuj膮c膮 p. magnetyczne jest indukcja
magnetyczna, okre艣laj膮ca oddzia艂ywanie pola na poruszaj膮cy si臋
艂adunek. Zale偶y ona r贸wnie偶 od w艂asno艣ci o艣rodka i tak dla
pr贸偶ni wynosi ona:

W o艣rodkach materialnych pole zewn臋trzne oddzia艂ywuje na elementarne obwody pr膮du zwi膮zane ze spinem i ruchem orbitalnym elektronu, uporz膮dkowuj膮c ich momenty magnetyczne w kierunku pola. W ten spos贸b powstaje pole dodatkowe, kt贸rego nat臋偶enie zwane namagnesowaniem r贸wna si臋 momentowi magnetycznemu jednostki obj臋to艣ci cia艂a:
 ,
gdzie:
,
gdzie:
 -
liczba atom贸w w jednostce obj臋to艣ci uporz膮dkowanych
w kierunku pola,
-
liczba atom贸w w jednostce obj臋to艣ci uporz膮dkowanych
w kierunku pola,
 -
wypadkowy moment magnetyczny atomu.
-
wypadkowy moment magnetyczny atomu.
Indukcja magnetyczna cia艂a wynosi zatem:

Indukcja magnetyczna mo偶e zosta膰 r贸wnie偶 wyra偶ona nast臋puj膮cym wzorem:



F - si艂a dzia艂aj膮ca w polu na przewodnik
I - nat臋偶enie pr膮du w tym przewodniku
l - d艂ugo艣膰 przewodnika
Jest ona wielko艣ci膮 wektorow膮 Kierunek tego wektora jest styczny do linii pola magnetycznego a zwrot wyznacza regu艂a prawej d艂oni.
Stosunek namagnesowania do nat臋偶enia pola zewn臋trznego nazywamy podatno艣ci膮 magnetyczn膮:
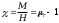
Ze wzgl臋du na jej warto艣膰 i zale偶no艣膰 od temperatury i nat臋偶enia pola dzielimy cia艂a na:
1. Diamagnetyki (cia艂a, np. gazy szlachetne, Zn, Cr, kt贸rych atomy maj膮 moment magnetyczny r贸wny zeru, a orbity elektron贸w w zewn臋trznym polu magnetycznym wykonuj膮 ruch precesyjny. Wytwarza on niewielki dodatkowy moment magnetyczny).
Paramagnetyki (np. powietrze, Al) - cia艂a, kt贸rych atomy lub cz膮steczki posiadaj膮 wypadkowy, r贸偶ny od zera moment magnetyczny. Cia艂a te nie wykazuj膮 namagnesowania w nieobecno艣ci pola zewn臋trznego. Podatno艣膰 magnetyczna paramagnetyk贸w jest odwrotnie proporcjonalna do temperatury bezwzgl臋dnej:

Wz贸r ten wyra偶a prawo Curie zgodnie z kt贸rym podatno艣膰 magnetyczna paramagnetyk贸w jest odwrotnie proporcjonalna do temperatury bezwzgl臋dnej. Jej warto艣膰 liczbowa jest rz臋du 10-6-10-2.
3. Ferro-, ferri-, antyferromagnetyki (cia艂a o strukturze domenowej; domeny s膮 to ma艂e obszary, w obr臋bie kt贸rych nast臋puje spontaniczne uporz膮dkowanie moment贸w magnetycznych tych cia艂. W ferromagnetykach Fe, Co, Ni, momenty magnetyczne wewn膮trz domeny s膮 zgodnie skierowane, w zwi膮zku z tym domeny maj膮 w艂asny silny moment magnetyczny.
Dla
ka偶dego ferromagnetyka istnieje okre艣lona temperatura
 zwana temperatur膮 (punktem) Curie, w kt贸rej ruch cieplny niszczy
struktur臋 domenow膮 i powoduje przej艣cie materia艂u w stan
paramagnetyczny. Inaczej m贸wi膮c jest to temperatura powy偶ej kt贸rej
traci on swoje zdolno艣ci ferromagnetyczne. Podatno艣膰 w tym stanie
spe艂nia prawo Curie - Weisa
zwana temperatur膮 (punktem) Curie, w kt贸rej ruch cieplny niszczy
struktur臋 domenow膮 i powoduje przej艣cie materia艂u w stan
paramagnetyczny. Inaczej m贸wi膮c jest to temperatura powy偶ej kt贸rej
traci on swoje zdolno艣ci ferromagnetyczne. Podatno艣膰 w tym stanie
spe艂nia prawo Curie - Weisa

Inne wielko艣ci okre艣laj膮ce p. magnetyczne:
- Strumie艅 indukcji magnetycznej, wyra偶ony wzorem:


- Nat臋偶enie pola magnetycznego:
 ,
gdzie:
,
gdzie:
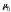 -
przenikalno艣膰 magnetyczna pr贸偶ni
-
przenikalno艣膰 magnetyczna pr贸偶ni
Nat臋偶enie pola magnetycznego mo偶emy wyrazi膰 r贸wnie偶 wzorem Biota - Savarta:

zale偶y
tylko od nat臋偶enia pr膮du i po艂o偶enia
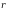 poszczeg贸lnych
odcink贸w przewodnika, wzgl臋dem rozpatrywanego pola.
poszczeg贸lnych
odcink贸w przewodnika, wzgl臋dem rozpatrywanego pola.
Przebieg do艣wiadczenia
|
Ux [mV] |
2y [cm] |
y [cm] |
|
U [mv] |
|
|
0,0 |
3,1 |
1,55 |
303,000 |
310 |
|
|
1,0 |
3,1 |
1,55 |
321,322 |
310 |
|
|
2,0 |
3,0 |
1,50 |
340,244 |
300 |
|
|
3,0 |
3,1 |
1,55 |
358,866 |
310 |
|
|
3,2 |
3,2 |
1,60 |
362,590 |
320 |
|
|
3,4 |
3,2 |
1,60 |
366,314 |
320 |
|
|
3,6 |
3,1 |
1,55 |
370,039 |
310 |
|
|
3,8 |
3,0 |
1,50 |
373,763 |
300 |
|
|
4,0 |
3,5 |
1,75 |
377,487 |
350 |
|
|
4,2 |
3,5 |
1,75 |
381,212 |
350 |
|
|
4,4 |
3,1 |
1,55 |
384,937 |
310 |
|
|
4,5 |
2,2 |
1,10 |
386,799 |
220 |
|
|
4,6 |
1,3 |
0,65 |
388,661 |
130 |
205,263 |
|
4,7 |
0,9 |
0,45 |
390,523 |
90 |
102,631 |
|
4,8 |
0,6 |
0,30 |
392,385 |
60 |
68,421 |
|
4,9 |
0,5 |
0,25 |
394,248 |
50 |
51,309 |
|
5,0 |
0,5 |
0,25 |
396,110 |
50 |
41,048 |
|
5,1 |
0,46 |
0,23 |
397,972 |
50 |
34,207 |

Wyszukiwarka