Dr Marzenna Zakrzewska
Instytut Psychologii UAM
ANALIZA WARIANCJI I ANALIZA REGRESJI WIELOKROTNEJ ÔÇô TO┼╗SAMO┼Ü─ć MODELI
Na ─çwiczeniach przy omawianiu jednoczynnikowej analizy wariancji pos┼éu┼╝yli┼Ťmy si─Ö przyk┼éadem zaczerpni─Ötym z ksi─ů┼╝ki Brzezi┼äskiego i Stachowskiego (1984)1. Przypomnijmy go w skr├│cie.
Ot├│┼╝ w pewnym fikcyjnym eksperymencie badaj─ůcym wp┼éyw wielko┼Ťci k─ůta widzenia na czas spostrzegania bod┼║ca otrzymano nast─Öpuj─ůce wyniki (tabela ze strony 38):
|
Poziomy czynnika A |
|||
|
a1 (900) |
a2 (1800) |
a3 (2700) |
a4 (3600) |
|
21 |
30 |
33 |
42 |
|
23 |
29 |
28 |
32 |
|
21 |
21 |
29 |
39 |
|
15 |
22 |
33 |
35 |
|
20 |
31 |
30 |
41 |
|
25 |
28 |
27 |
38 |
|
27 |
26 |
25 |
37 |
|
16 |
25 |
29 |
40 |
|
22 |
27 |
25 |
39 |
|
17 |
31 |
26 |
38 |
Symbole a1, a2, a3 oraz a4 oznaczaj─ů cztery r├│┼╝ne k─ůty widzenia w stopniach, za┼Ť czasy spostrzegania bod┼║ca wyra┼╝ono w sekundach pomno┼╝onych przez 102.
Mamy tu wi─Öc cztery r├│wnoliczne (n=10) grupy os├│b badanych. Ka┼╝da z grup wykonywa┼éa zadanie (badani naciskali przycisk, gdy spostrzegli bodziec ┼Ťwietlny) w r├│┼╝nych warunkach eksperymentalnych (r├│┼╝ne wielko┼Ťci k─ůta widzenia). Problem badawczy, jaki stara┼é si─Ö rozwi─ůza─ç eksperymentator mo┼╝na sformu┼éowa─ç nast─Öpuj─ůco:
Czy czas spostrzegania bod┼║ca zale┼╝y od k─ůta widzenia?
Taki problem badawczy mo┼╝na analizowa─ç odwo┼éuj─ůc si─Ö:
- albo do modelu analizy wariancji (ANOVA)
- albo do modelu analizy regresji wielokrotnej (MCR)
Po zastosowaniu obu modeli otrzymamy takie same wyniki, a więc sformułujemy takie same wnioski.
Przyjrzyjmy si─Ö wi─Öc, jak za pomoc─ů pakietu statystycznego SPSS poradzi─ç sobie w obu wy┼╝ej wymienionych modelach z weryfikacj─ů hipotezy, kt├│ra brzmi:
Czas spostrzegania bod┼║ca zale┼╝y od k─ůta widzenia.
I. MODEL ANALIZY WARIANCJI
Najpierw zajmijmy si─Ö modelem analizy wariancji. Poka┼╝emy, jak wprowadzi─ç dane do SPSS-a, jak uruchomi─ç w pakiecie odpowiednie procedury i jak zinterpretowa─ç uzyskany wydruk.
1. Wprowadzenie danych
Dane do jednoczynnikowej analizy wariancji powinny zosta─ç wprowadzone w dw├│ch kolumnach.
Pierwsza z nich mo┼╝e zosta─ç nazwana ÔÇ×grupaÔÇŁ. Kolejne liczby (od 1 do 4), kt├│re pojawi┼éy si─Ö w tej kolumnie oznaczaj─ů numer grupy eksperymentalnej. Osoby oznaczone liczb─ů ÔÇ×1ÔÇŁ to osoby, kt├│rym przyporz─ůdkowano k─ůt widzenia o wielko┼Ťci 900, osobom oznaczonym liczb─ů ÔÇ×2ÔÇŁ przyporz─ůdkowano k─ůt 1800, oznaczonym liczb─ů ÔÇ×3ÔÇŁ k─ůt 2700, za┼Ť oznaczonym liczb─ů ÔÇ×4ÔÇŁ k─ůt 3600. Wykorzystanym tu liczbom mo┼╝na rzecz jasna przypisa─ç etykiety, takie jak na przyk┼éad 900, 1800, 2700 i 3600 lub a1, a2, a3 oraz a4. Druga zmienna zawiera czas spostrzegania bod┼║ca dla ka┼╝dej osoby badanej i mo┼╝e zosta─ç na przyk┼éad nazwana ÔÇ×czasÔÇŁ. Opisany tutaj spos├│b zapisania danych w pakiecie SPSS ilustruje poni┼╝sza tabela:
|
|
Grupa |
czas |
|
1 |
1 |
21 |
|
2 |
1 |
23 |
|
3 |
1 |
21 |
|
4 |
1 |
15 |
|
5 |
1 |
20 |
|
6 |
1 |
25 |
|
7 |
1 |
27 |
|
8 |
1 |
16 |
|
9 |
1 |
22 |
|
10 |
1 |
17 |
|
11 |
2 |
30 |
|
12 |
2 |
29 |
|
13 |
2 |
21 |
|
14 |
2 |
22 |
|
15 |
2 |
31 |
|
16 |
2 |
28 |
|
17 |
2 |
26 |
|
18 |
2 |
25 |
|
19 |
2 |
27 |
|
20 |
2 |
31 |
|
21 |
3 |
33 |
|
22 |
3 |
28 |
|
23 |
3 |
29 |
|
24 |
3 |
33 |
|
25 |
3 |
30 |
|
26 |
3 |
27 |
|
27 |
3 |
25 |
|
28 |
3 |
29 |
|
29 |
3 |
25 |
|
30 |
3 |
26 |
|
31 |
4 |
42 |
|
32 |
4 |
32 |
|
33 |
4 |
39 |
|
34 |
4 |
35 |
|
35 |
4 |
41 |
|
36 |
4 |
38 |
|
37 |
4 |
37 |
|
38 |
4 |
40 |
|
39 |
4 |
39 |
|
40 |
4 |
38 |
2. Uruchomienie jednoczynnikowej analizy wariancji w pakiecie SPSS
Aby uruchomi─ç analiz─Ö wariancji nale┼╝y wybra─ç nast─Öpuj─ůce elementy w menu SPSS-a:
- Analiza Ôćĺ Og├│lny model liniowy Ôćĺ Jednej zmiennejÔÇŽ
- do okienka Zmienna zale┼╝na przenosimy zmienn─ů ÔÇ×czasÔÇŁ
- do okienka Czynniki sta┼ée przenosimy zmienn─ů ÔÇ×grupaÔÇŁ
- naciskamy przycisk Opcje i wybieramy Statystyki opisowe oraz Oceny wielko┼Ťci efektu
- naciskamy przycisk Post hoc, przenosimy zmienn─ů ÔÇ×grupaÔÇŁ z okienka Czynniki do okienka Testy post hoc dla i wybieramy Tukey
- naciskamy przycisk Wykresy i przenosimy zmienn─ů ÔÇ×grupaÔÇŁ z okienka Czynniki do okienka O┼Ť pozioma
Po klikni─Öciu przycisku OK otrzymamy nast─Öpuj─ůcy wydruk:
Analiza wariancji jednej zmiennej (UNIANOVA)
Czynniki mi─Ödzyobiektowe
|
|
Etykieta warto┼Ťci |
N |
|
|
grupa (czynnik) |
1,00 |
a1 |
10 |
|
2,00 |
a2 |
10 |
|
|
3,00 |
a3 |
10 |
|
|
4,00 |
a4 |
10 |
|
Statystyki opisowe
Zmienna zale┼╝na: czas (zm. zale┼╝na)
|
grupa (czynnik) |
Średnia |
Odchylenie standardowe |
N |
|
a1 |
20,7000 |
3,86005 |
10 |
|
a2 |
27,0000 |
3,52767 |
10 |
|
a3 |
28,5000 |
2,91548 |
10 |
|
a4 |
38,1000 |
2,92309 |
10 |
|
Ogółem |
28,5750 |
7,07429 |
40 |
Testy efekt├│w mi─Ödzyobiektowych
Zmienna zale┼╝na: czas (zm. zale┼╝na)
|
┼╣r├│d┼éo zmienno┼Ťci |
Typ III sumy kwadrat├│w |
df |
Średni kwadrat |
F |
Istotno┼Ť─ç |
Czastkowe Eta kwadrat |
|
Model skorygowany |
1552,275(a) |
3 |
517,425 |
46,627 |
,000 |
,795 |
|
Stała |
32661,225 |
1 |
32661,225 |
2943,189 |
,000 |
,988 |
|
grupa |
1552,275 |
3 |
517,425 |
46,627 |
,000 |
,795 |
|
B┼é─ůd |
399,500 |
36 |
11,097 |
|
|
|
|
Ogółem |
34613,000 |
40 |
|
|
|
|
|
Ogółem skorygowane |
1951,775 |
39 |
|
|
|
|
a R kwadrat = ,795 (Skorygowane R kwadrat = ,778)
Testy post hoc
grupa (czynnik)
Por├│wnania wielokrotne
Zmienna zale┼╝na: czas (zm. zale┼╝na)
Test Tukey'a HSD
|
(I) grupa (czynnik) |
(J) grupa (czynnik) |
R├│┼╝nica ┼Ťrednich (I-J) |
B┼é─ůd standardowy |
Istotno┼Ť─ç |
95% przedzia┼é ufno┼Ťci |
|
|
Dolna granica |
G├│rna granica |
|||||
|
a1 |
a2 |
-6,3000(*) |
1,48978 |
,001 |
-10,3123 |
-2,2877 |
|
a3 |
-7,8000(*) |
1,48978 |
,000 |
-11,8123 |
-3,7877 |
|
|
a4 |
-17,4000(*) |
1,48978 |
,000 |
-21,4123 |
-13,3877 |
|
|
a2 |
a1 |
6,3000(*) |
1,48978 |
,001 |
2,2877 |
10,3123 |
|
a3 |
-1,5000 |
1,48978 |
,746 |
-5,5123 |
2,5123 |
|
|
a4 |
-11,1000(*) |
1,48978 |
,000 |
-15,1123 |
-7,0877 |
|
|
a3 |
a1 |
7,8000(*) |
1,48978 |
,000 |
3,7877 |
11,8123 |
|
a2 |
1,5000 |
1,48978 |
,746 |
-2,5123 |
5,5123 |
|
|
a4 |
-9,6000(*) |
1,48978 |
,000 |
-13,6123 |
-5,5877 |
|
|
a4 |
a1 |
17,4000(*) |
1,48978 |
,000 |
13,3877 |
21,4123 |
|
a2 |
11,1000(*) |
1,48978 |
,000 |
7,0877 |
15,1123 |
|
|
a3 |
9,6000(*) |
1,48978 |
,000 |
5,5877 |
13,6123 |
|
W oparciu o ┼Ťrednie obserwowane.
* R├│┼╝nica ┼Ťrednich jest istotna na poziomie ,05.
Grupy jednorodne
czas (zm. zale┼╝na)
Test Tukey'a HSD
|
grupa (czynnik) |
N |
Grupy |
||
|
1 |
2 |
3 |
||
|
A1 |
10 |
20,7000 |
|
|
|
A2 |
10 |
|
27,0000 |
|
|
A3 |
10 |
|
28,5000 |
|
|
A4 |
10 |
|
|
38,1000 |
|
Istotno┼Ť─ç |
|
1,000 |
,746 |
1,000 |
Przedstawione s─ů ┼Ťrednie grupowe dla grup jednorodnych. W oparciu o Typ III sumy kwadrat├│w. Sk┼éadnikiem b┼é─Öd├│w jest ┼Üredni kwadrat (B┼é─ůd) = 11,097.
a U┼╝yto ┼Ťredniej harmonicznej wielko┼Ťci pr├│by = 10,000
b Alfa = ,05.
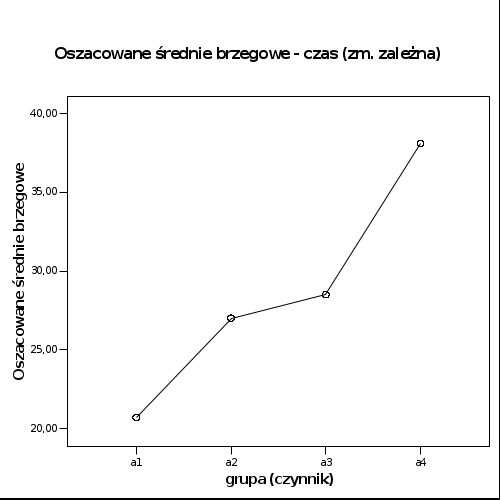
Wykresy profili
3. Interpretacja wydruku
Analiza wariancji jest technik─ů r├│┼╝nicow─ů, dlatego te┼╝ weryfikuje hipotezy o r├│┼╝nicach pomi─Ödzy grupami. Hipoteza zerowa do naszego przyk┼éadu powinna wi─Öc zosta─ç sformu┼éowana nast─Öpuj─ůco:
Grupy os├│b badanych r├│┼╝ni─ůce si─Ö k─ůtem widzenia r├│┼╝ni─ů si─Ö czasem spostrzegania bod┼║ca.
(co oczywi┼Ťcie w tym kontek┼Ťcie oznacza, ┼╝e od k─ůta widzenia zale┼╝y czas spostrzegania bod┼║ca).
Bardziej formalnie
hipotez─Ö t─Ö mo┼╝na wyrazi─ç w spos├│b nast─Öpuj─ůcy:
 [brak
zr├│┼╝nicowania (= wariancji) pomi─Ödzy grupami]
[brak
zr├│┼╝nicowania (= wariancji) pomi─Ödzy grupami]
Testu weryfikuj─ůcego t─Ö hipotez─Ö szukamy w tabeli zatytu┼éowanej ÔÇ×Testy efekt├│w mi─ÖdzyobiektowychÔÇŁ w wierszu dla zmiennej ÔÇ×grupaÔÇŁ. Efekt tego testu mo┼╝na podsumowa─ç nast─Öpuj─ůco: F=46,627; dfgrupa=3; dfb┼é─ůd=36; p<0,001. Wynika z niego, ┼╝e mamy podstawy do odrzucenia hipotezy zerowej o braku r├│┼╝nic pomi─Ödzy grupami na rzecz hipotezy alternatywnej. Taki wniosek statystyczny oznacza, ┼╝e mamy do czynienia ze zr├│┼╝nicowaniem pomi─Ödzy analizowanymi grupami.
┼Ürednie i odchylenia standardowe dla czasu potrzebnego do spostrze┼╝enia bod┼║ca ┼Ťwietlnego dla ka┼╝dej z czterech badanych grup eksperymentalnych odnajdziemy w tabeli zatytu┼éowanej ÔÇ×Statystyki opisoweÔÇŁ. Dodatkow─ů wizualizacj─ů r├│┼╝nic pomi─Ödzy ┼Ťrednimi dla czterech grup jest diagram zatytu┼éowany ÔÇ×Wykresy profiliÔÇŁ. Mo┼╝emy si─Ö przekona─ç, ┼╝e najni┼╝sz─ů ┼Ťredni─ů osi─ůgn─Ö┼éa grupa a1, najwy┼╝sz─ů grupa a4, a ┼Ťrednie grup a2 i a3 s─ů wi─Öksze od a1 i mniejsze od a4, ale niewiele si─Ö od siebie r├│┼╝ni─ů. Czy wi─Öc wszystkie cztery grupy badanych r├│┼╝ni─ů si─Ö pomi─Ödzy sob─ů? Odpowied┼║ na to pytanie znajdziemy w tabeli zatytu┼éowanej ÔÇ×Testy post hocÔÇŁ (kolumna z /nag┼é├│wkiem ÔÇ×Istotno┼Ť─çÔÇŁ).
- r├│┼╝nica pomi─Ödzy grup─ů a1 i a2 jest istotna statystycznie (p=0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a1 i a3 jest istotna statystycznie (p<0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a1 i a4 jest istotna statystycznie (p<0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a2 i a3 jest nieistotna statystycznie (p=0,746)
- r├│┼╝nica pomi─Ödzy grup─ů a2 i a4 jest istotna statystycznie (p<0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a3 i a4 jest istotna statystycznie (p<0,001)
Tak wi─Öc grupy a2 oraz a3 od siebie si─Ö nie r├│┼╝ni─ů, ale maj─ů czas spostrzegania bod┼║ca d┼éu┼╝szy ni┼╝ grupa a1 i kr├│tszy ni┼╝ grupa a4.
Wyniki eksperymentu potwierdzaj─ů wi─Öc hipotez─Ö o zale┼╝no┼Ťci czasu spostrzegania bod┼║ca od k─ůta widzenia. Sprawd┼║my jeszcze, jaki procent wariancji zmiennej zale┼╝nej mo┼╝na wyt┼éumaczy─ç wp┼éywem zmiennej niezale┼╝nej (tu: czynnika). Na wydruku analizy wariancji warto┼Ť─ç ta pojawia si─Ö w dw├│ch miejscach:
Pod tabel─ů ÔÇ×Testy efekt├│w mi─ÖdzyobiektowychÔÇŁ mamy podan─ů warto┼Ť─ç R-kwadrat=0,759. Ta warto┼Ť─ç pomno┼╝ona razy 100% da nam procent wariancji zmiennej zale┼╝nej t┼éumaczony przez wszystkie wykorzystane zmienne niezale┼╝ne (=czynniki)
W tabeli ÔÇ×Testy efekt├│w mi─ÖdzyobiektowychÔÇŁ, w kolumnie ÔÇ×cz─ůstkowe Eta kwadratÔÇŁ mamy te sam─ů warto┼Ť─ç r├│wn─ů 0,759. Ta warto┼Ť─ç pomno┼╝ona razy 100% da nam procent wariancji zmiennej zale┼╝nej t┼éumaczony przez pojedyncz─ů zmienn─ů niezale┼╝n─ů (=czynnik)
W przypadku jednoczynnikowej analizy wariancji R-kwadrat i cz─ůstkowe Eta kwadrat dla czynnika b─Öd─ů rzecz jasna t─ů sam─ů warto┼Ťci─ů. Dodajmy jeszcze, ┼╝e w analizie wariancji wska┼║nik eta-kwadrat liczymy dziel─ůc SSgrupa przez SSog├│┼éem skorygowane [1552,275/1951,775=0,759].
Interpretacj─Ö mo┼╝emy wiec zako┼äczy─ç wnioskiem, ┼╝e k─ůt widzenia t┼éumaczy 75,9 procenta wariancji czasu spostrzegania bod┼║ca.
II. MODEL ANALIZY REGRESJI
Spr├│bujmy teraz te same wyniki zanalizowa─ç w modelu regresji wielokrotnej.
W analizie wariancji czynnik (=zmienna niezale┼╝na) zawsze ÔÇô bez wzgl─Ödu na swoj─ů natur─Ö ÔÇô jest traktowany jak zmienna jako┼Ťciowa. Je┼╝eli w analizie regresji pojawi si─Ö jako┼Ťciowa zmienna niezale┼╝na, to nale┼╝y j─ů zakodowa─ç.
Je┼╝eli nasza zmienna niezale┼╝na nazwana ÔÇ×grupaÔÇŁ zosta┼éaby wprowadzona do r├│wnania regresji w nie zmienionej formie, to u┼╝yte w pliku liczby zosta┼éyby potraktowane tak, jakby wyra┼╝a┼éy jednostki na skali co najmniej interwa┼éowej (osoba z grupy a2 mia┼éaby o dwie jednostki ni┼╝szy wynik od osoby z grupy a4).
Prze┼Ťled┼║my wi─Öc najpierw spos├│b kodowania zmiennej jako┼Ťciowej za pomoc─ů SPSS-a a nast─Öpnie wydruk analizy regresji, do kt├│rej wprowadzimy t─Ö zakodowan─ů zmienn─ů. Skupimy si─Ö na dw├│ch najbardziej rozpowszechnionych systemach, kt├│re nazwane zosta┼éy kodowaniem zero-jedynkowym i kodowaniem quasi-eksperymentalnym.
A. KODOWANIE ZERO-JEDYNKOWE
1. Kodowanie zero-jedynkowe zmiennej jako┼Ťciowej
Jak pisze profesor Brzezi┼äski (s. 371) ÔÇ×Obja┼Ťni─Ö teraz, na czym polega zabieg kodowania zero-jedynkowego (ang. dummy coding) p-kategorialnej zmiennej jako┼Ťciowej. Kodowanie polega na utworzeniu m (gdzie m = p ÔÇô 1) nowych zmiennych (wektor├│w) instrumentalnych. Te nowe zmienne powstaj─ů w ten spos├│b, ┼╝e osobom z danej i-tej kategorii (i-tej grupy por├│wnawczej) przypisujemy jedynki, a osobom z pozosta┼éych kategorii przypisujemy zera. Ostatnia kategoria p (p-ta grupa por├│wnawcza) reprezentowana jest we wszystkich m wektorach przez same zera.ÔÇŁ2
Dla naszych danych oznacza to, ┼╝e dla czterech kategorii zmiennej niezale┼╝nej (cztery grupy os├│b badanych) b─Ödziemy musieli utworzy─ç trzy wektory instrumentalne (T1, T2 i T3).
- osoby z grupy a1 na wektorze T1 b─Öd─ů mia┼éy jedynki, a na pozosta┼éych wektorach zera (T1=1 T2=0 i T3=0)
- osoby z grupy a2 na wektorze T2 b─Öd─ů mia┼éy jedynki, a na pozosta┼éych wektorach zera (T1=0 T2=1 i T3=0)
- osoby z grupy a3 na wektorze T3 b─Öd─ů mia┼éy jedynki, a na pozosta┼éych wektorach zera (T1=0 T2=0 i T3=1)
- osoby z grupy a4 na wszystkich trzech wektorach b─Öd─ů mia┼éy zera (T1=0 T2=0 i T3=0)
W ten spos├│b cztery grupy b─Öd─ů odr├│┼╝nialne jedynie wtedy, gdy we┼║miemy pod uwag─Ö wszystkie trzy zmienne instrumentalne r├│wnocze┼Ťnie:
- grupa a1 ÔÇô sekwencja 1 0 0
- grupa a2 ÔÇô sekwencja 0 1 0
- grupa a3 ÔÇô sekwencja 0 0 1
- grupa a4 ÔÇô sekwencja 0 0 0
Aby zakodowa─ç nasz─ů zmienn─ů jako┼Ťciow─ů (stworzy─ç trzy nowe zmienne instrumentalne) nale┼╝y wybra─ç nast─Öpuj─ůce elementy w menu SPSS-a:
1. Najpierw tworzymy pierwsz─ů zmienn─ů instrumentaln─ů (T1) na kt├│rej tylko grupa a1 ma ÔÇ×1ÔÇŁ, a reszta ÔÇ×0ÔÇŁ
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Oblicz warto┼ŤciÔÇŽ
- do okienka Zmienna wynikowa wpisujemy nazw─Ö nowego wektora: ÔÇ×T1ÔÇŁ
- do okienka Wyra┼╝enie numeryczne wpisujemy liczb─Ö ÔÇ×1ÔÇŁ
- naciskamy przycisk Je┼╝eli i zaznaczamy opcj─Ö Uwzgl─Ödnij, je┼Ťli obserwacja spe┼énia warunek
- przenosimy z listy zmiennych do pod┼Ťwietlonego ju┼╝ teraz okienka zmienn─ů ÔÇ×grupaÔÇŁ i korzystaj─ůc z klawiatury w oknie dialogowym albo z klawiatury komputera dopisujemy warunek logiczny ÔÇ×= 1ÔÇŁ
- naciskamy przycisk Dalej oraz OK
SPSS dopisze do pliku now─ů zmienn─ů o nazwie ÔÇ×T1ÔÇŁ i osobom z grupy a1 przypisze na niej jedynki. Pozosta┼ée osoby b─Öd─ů mia┼éy na tej zmiennej brakuj─ůce warto┼Ťci (puste kratki).
2. Nast─Öpnie tworzymy drug─ů zmienn─ů instrumentaln─ů (T2) na kt├│rej tylko grupa a2 ma ÔÇ×1ÔÇŁ, a reszta ÔÇ×0ÔÇŁ.
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Oblicz warto┼ŤciÔÇŽ
- do okienka Zmienna wynikowa wpisujemy nazw─Ö nowego wektora: ÔÇ×T2ÔÇŁ
- do okienka Wyra┼╝enie numeryczne wpisujemy liczb─Ö ÔÇ×1ÔÇŁ
- naciskamy przycisk Je┼╝eli i zaznaczamy opcj─Ö Uwzgl─Ödnij, je┼Ťli obserwacja spe┼énia warunek
- przenosimy z listy zmiennych do pod┼Ťwietlonego ju┼╝ teraz okienka zmienn─ů ÔÇ×grupaÔÇŁ i korzystaj─ůc z klawiatury w oknie dialogowym albo z klawiatury komputera dopisujemy warunek logiczny ÔÇ×= 2ÔÇŁ
- naciskamy przycisk Dalej oraz OK
SPSS dopisze do pliku nast─Öpn─ů zmienn─ů, tym razem o nazwie ÔÇ×T2ÔÇŁ i osobom z grupy a2 przypisze na niej jedynki. Pozosta┼ée osoby b─Öd─ů mia┼éy na tej zmiennej brakuj─ůce warto┼Ťci (puste kratki).
3. Teraz tworzymy trzeci─ů zmienn─ů instrumentaln─ů (T3) na kt├│rej tylko grupa a3 ma ÔÇ×1ÔÇŁ, a reszta ÔÇ×0ÔÇŁ.
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Oblicz warto┼ŤciÔÇŽ
- do okienka Zmienna wynikowa wpisujemy nazw─Ö nowego wektora: ÔÇ×T3ÔÇŁ
- do okienka Wyra┼╝enie numeryczne wpisujemy liczb─Ö ÔÇ×1ÔÇŁ
- naciskamy przycisk Je┼╝eli i zaznaczamy opcj─Ö Uwzgl─Ödnij, je┼Ťli obserwacja spe┼énia warunek
- przenosimy z listy zmiennych do pod┼Ťwietlonego ju┼╝ teraz okienka zmienn─ů ÔÇ×grupaÔÇŁ i korzystaj─ůc z klawiatury w oknie dialogowym albo z klawiatury komputera dopisujemy warunek logiczny ÔÇ×= 3ÔÇŁ
- naciskamy przycisk Dalej oraz OK
SPSS dopisze do pliku nast─Öpn─ů zmienn─ů, tym razem o nazwie ÔÇ×T3ÔÇŁ i osobom z grupy a3 przypisze na niej jedynki. Pozosta┼ée osoby b─Öd─ů mia┼éy na tej zmiennej brakuj─ůce warto┼Ťci (puste kratki).
4. Teraz trzeba wype┼éni─ç warto┼Ťciami ÔÇ×0ÔÇŁ wszystkie puste kratki dla zmiennych T1, T2 i T3.
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Rekoduj Ôćĺ Na te same zmienneÔÇŽ
- do okienka Zmienne numeryczne przenosimy nowe zmienne: ÔÇ×T1, T2 i T3ÔÇŁ
- naciskamy przycisk Warto┼Ťci ┼║r├│d┼éowe i wynikowe
- w lewej cz─Ö┼Ťci okna dialogowego zatytu┼éowanej Warto┼Ťci ┼║r├│d┼éowe zaznaczamy opcj─Ö Systemowy brak danych
- w prawej cz─Ö┼Ťci okna dialogowego zatytu┼éowanej Warto┼Ťci wynikowe zaznaczamy opcj─Ö Warto┼Ť─ç i do pustego okienka wpisujemy liczb─Ö ÔÇ×0ÔÇŁ
- naciskamy przyciski Dodaj, Dalej oraz OK
SPSS uzupe┼éni zerami wszystkie brakuj─ůce dane (puste kratki) w zmiennych T1, T2 i T3.
Efekt wyżej przedstawionych przekształceń ilustruje poniższa tabela:
|
|
Grupa |
czas |
T1 |
T2 |
T3 |
|
1 |
1 |
21 |
1 |
0 |
0 |
|
2 |
1 |
23 |
1 |
0 |
0 |
|
3 |
1 |
21 |
1 |
0 |
0 |
|
4 |
1 |
15 |
1 |
0 |
0 |
|
5 |
1 |
20 |
1 |
0 |
0 |
|
6 |
1 |
25 |
1 |
0 |
0 |
|
7 |
1 |
27 |
1 |
0 |
0 |
|
8 |
1 |
16 |
1 |
0 |
0 |
|
9 |
1 |
22 |
1 |
0 |
0 |
|
10 |
1 |
17 |
1 |
0 |
0 |
|
11 |
2 |
30 |
0 |
1 |
0 |
|
12 |
2 |
29 |
0 |
1 |
0 |
|
13 |
2 |
21 |
0 |
1 |
0 |
|
14 |
2 |
22 |
0 |
1 |
0 |
|
15 |
2 |
31 |
0 |
1 |
0 |
|
16 |
2 |
28 |
0 |
1 |
0 |
|
17 |
2 |
26 |
0 |
1 |
0 |
|
18 |
2 |
25 |
0 |
1 |
0 |
|
19 |
2 |
27 |
0 |
1 |
0 |
|
20 |
2 |
31 |
0 |
1 |
0 |
|
21 |
3 |
33 |
0 |
0 |
1 |
|
22 |
3 |
28 |
0 |
0 |
1 |
|
23 |
3 |
29 |
0 |
0 |
1 |
|
24 |
3 |
33 |
0 |
0 |
1 |
|
25 |
3 |
30 |
0 |
0 |
1 |
|
26 |
3 |
27 |
0 |
0 |
1 |
|
27 |
3 |
25 |
0 |
0 |
1 |
|
28 |
3 |
29 |
0 |
0 |
1 |
|
29 |
3 |
25 |
0 |
0 |
1 |
|
30 |
3 |
26 |
0 |
0 |
1 |
|
31 |
4 |
42 |
0 |
0 |
0 |
|
32 |
4 |
32 |
0 |
0 |
0 |
|
33 |
4 |
39 |
0 |
0 |
0 |
|
34 |
4 |
35 |
0 |
0 |
0 |
|
35 |
4 |
41 |
0 |
0 |
0 |
|
36 |
4 |
38 |
0 |
0 |
0 |
|
37 |
4 |
37 |
0 |
0 |
0 |
|
38 |
4 |
40 |
0 |
0 |
0 |
|
39 |
4 |
39 |
0 |
0 |
0 |
|
40 |
4 |
38 |
0 |
0 |
0 |
2. Uruchomienie analizy regresji w pakiecie SPSS
Aby uruchomi─ç analiz─Ö regresji nale┼╝y wybra─ç nast─Öpuj─ůce elementy w menu SPSS-a:
- Analiza Ôćĺ Regresja Ôćĺ LiniowaÔÇŽ
- do okienka Zmienna zale┼╝na przenosimy zmienn─ů ÔÇ×czasÔÇŁ
- do okienka Zmienne niezale┼╝ne przenosimy wektory instrumentalne ÔÇ×T1, T2 i T3ÔÇŁ
- upewnijmy si─Ö, ┼╝e w okienku Metoda znajduje si─Ö ÔÇ×Metoda wprowadzaniaÔÇŁ (zaznaczana domy┼Ťlnie)
Po klikni─Öciu przycisku OK otrzymamy nast─Öpuj─ůcy wydruk:
Regresja
Zmienne wprowadzone/usuni─Öte(b)
|
Model |
Zmienne wprowadzone |
Zmienne usuni─Öte |
Metoda |
|
1 |
T3 - (1) grupa a3, T2 - (1) grupa a2, T1 - (1) grupa a1(a) |
. |
Wprowadzanie |
a Wszystkie wyspecyfikowane zmienne zostały wprowadzone.
b Zmienna zale┼╝na: czas (zm. zale┼╝na)
Model - Podsumowanie
|
Model |
R |
R-kwadrat |
Skorygowane R-kwadrat |
B┼é─ůd standardowy oszacowania |
|
1 |
,892(a) |
,795 |
,778 |
3,33125 |
a Predyktory: (Stała), T3 - (1) grupa a3, T2 - (1) grupa a2, T1 - (1) grupa a1
Analiza wariancji(b)
|
Model |
|
Suma kwadrat├│w |
df |
Średni kwadrat |
F |
Istotno┼Ť─ç |
|
1 |
Regresja |
1552,275 |
3 |
517,425 |
46,627 |
,000(a) |
|
Reszta |
399,500 |
36 |
11,097 |
|
|
|
|
Ogółem |
1951,775 |
39 |
|
|
|
a Predyktory: (Stała), T3 - (1) grupa a3, T2 - (1) grupa a2, T1 - (1) grupa a1
b Zmienna zale┼╝na: czas (zm. zale┼╝na)
Współczynniki(a)
|
Model |
|
Współczynniki niestandaryzowane |
Współczynniki standaryzowane |
t |
Istotno┼Ť─ç |
|
|
B |
B┼é─ůd standardowy |
Beta |
||||
|
1 |
(Stała) |
38,100 |
1,053 |
|
36,167 |
,000 |
|
T1 - (1) grupa a1 |
-17,400 |
1,490 |
-1,079 |
-11,680 |
,000 |
|
|
T2 - (1) grupa a2 |
-11,100 |
1,490 |
-,688 |
-7,451 |
,000 |
|
|
T3 - (1) grupa a3 |
-9,600 |
1,490 |
-,595 |
-6,444 |
,000 |
|
a Zmienna zale┼╝na: czas (zm. zale┼╝na)
3. Interpretacja wydruku
Analiza regresji jest technik─ů zale┼╝no┼Ťciow─ů, dlatego te┼╝ weryfikuje hipotezy o zale┼╝no┼Ťciach pomi─Ödzy zmiennymi. Hipoteza zerowa do naszego przyk┼éadu powinna wi─Öc zosta─ç sformu┼éowana nast─Öpuj─ůco:
Brak zwi─ůzku pomi─Ödzy k─ůtem widzenia i czasem spostrzegania bod┼║ca.
(co oczywi┼Ťcie oznacza, ┼╝e ludzie przy r├│┼╝nych k─ůtach widzenia r├│┼╝ni─ů si─Ö czasem spostrzegania bod┼║ca).
Poniewa┼╝ nasze trzy zmienne instrumentalne tworz─ů de facto jedn─ů zmienn─ů jako┼Ťciow─ů (zakodowan─ů), nie b─Öd─ů nas interesowa┼éy zwi─ůzki pomi─Ödzy pojedynczymi wektorami (T1, T2 oraz T3) i zmienn─ů zale┼╝n─ů. Og├│lny wska┼║nik R-kwadrat informuje nas o tym, ile wariancji zmiennej zale┼╝nej (czasu spostrzegania bod┼║ca) wyja┼Ťnia zmienna niezale┼╝na (k─ůt widzenia).
Wska┼║nik R-kwadrat znajdziemy w tabeli ÔÇ×Model ÔÇô PodsumowanieÔÇŁ. Jego warto┼Ť─ç wynosi 0,795, a to oznacza, ┼╝e zmienna zale┼╝na t┼éumaczy 79,5% wariancji zmiennej zale┼╝nej. Por├│wnajmy t─Ö warto┼Ť─ç ze wska┼║nikiem R-kwadrat lub Eta-kwadrat z analizy wariancji. S─ů one identyczne.
Por├│wnajmy teraz zawarto┼Ť─ç tabel:
- ÔÇ×Testy efekt├│w mi─ÖdzyobiektowychÔÇŁ z wydruku analizy wariancji (wiersze: ÔÇ×grupaÔÇŁ, ÔÇ×b┼é─ůdÔÇŁ oraz ÔÇ×og├│┼éem skorygowaneÔÇŁ)
- ÔÇ×Analiza wariancjiÔÇŁ z wydruku analizy regresji
Zawieraj─ů one dok┼éadnie te same liczby. Nic w tym dziwnego, poniewa┼╝ ÔÇô jak staramy si─Ö wykaza─ç ÔÇô model analizy wariancji i model analizy regresji s─ů to┼╝same.
- Test F w analizie wariancji testuje, czy wariancja zmiennej zale┼╝nej (=czas spostrzegania bod┼║ca) wyja┼Ťniona przez czynnik (zmienn─ů niezale┼╝n─ů = k─ůt widzenia) jest wi─Öksza od tej wariancji, kt├│rej ten czynnik nie wyja┼Ťnia (tzw. wariancji b┼é─Ödu)
- Test F w analizie regresji testuje, czy wariancja zmiennej zale┼╝nej (=czas spostrzegania bod┼║ca) wyja┼Ťniona przez zmienn─ů niezale┼╝n─ů (k─ůt widzenia) jest wi─Öksza od tej wariancji, kt├│rej ta zmienna nie wyja┼Ťnia (tzw. wariancja resztowa) ÔÇô jest to test istotno┼Ťci warto┼Ťci R-kwadrat
Nic wi─Öc w tym dziwnego, ┼╝e obie tabele zawieraj─ů te same warto┼Ťci. Wynik tego testu (F=46,627; dfregresja=3; dfreszta=36; p<0,001) wskazuje, ze odrzucamy hipotez─Ö zerow─ů o braku zwi─ůzku pomi─Ödzy zmienn─ů zale┼╝n─ů (czasem spostrzegania bod┼║ca) i zmienn─ů niezale┼╝n─ů (k─ůtem widzenia). Wnioski z analizy wariancji i z analizy regresji nie r├│┼╝ni─ů si─Ö.
┼╗eby do ko┼äca zrozumie─ç to┼╝samo┼Ť─ç obu omawianych modeli warto jeszcze zwr├│ci─ç uwag─Ö na r├│wnanie regresji. W analizowanym przypadku owo r├│wnanie przyjmie nast─Öpuj─ůc─ů posta─ç:
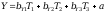
Z tabeli ÔÇ×Wsp├│┼éczynnikiÔÇŁ mo┼╝emy odczyta─ç warto┼Ťci wsp├│┼éczynnik├│w b (w tabeli kolumna z nag┼é├│wkiem ÔÇ×BÔÇŁ) i uzupe┼éni─ç r├│wnanie. Liczba znajduj─ůca si─Ö w wierszu ÔÇ×(sta┼éa)ÔÇŁ i w kolumnie ÔÇ×BÔÇŁ to warto┼Ť─ç wsp├│┼éczynnika a w r├│wnaniu regresji. Nasze r├│wnanie b─Ödzie wi─Öc mia┼éo posta─ç:
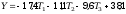
Co te wsp├│┼éczynniki oznaczaj─ů? Jak je interpretowa─ç? ┼╗eby je mo┼╝na by┼éo sensownie interpretowa─ç trzeba pami─Öta─ç o tym, ┼╝e przy kodowaniu zero-jedynkowym zawsze jedna z analizowanych grup zostanie potraktowana jako grupa odniesienia, do kt├│rej b─Ödziemy por├│wnywa─ç wszystkie pozosta┼ée. Mo┼╝e to by─ç dowolna grupa. My jednak musimy dokona─ç jej wyboru ju┼╝ na etapie kodowania zmiennej jako┼Ťciowej. B─Ödzie to bowiem zawsze ta grupa, kt├│ra ma na wszystkich zmiennych instrumentalnych zera. W naszym przypadku grup─ů referencyjn─ů sta┼éa si─Ö grupa a4, bo ona w┼éa┼Ťnie charakteryzuje si─Ö sekwencj─ů 0, 0, 0 na wektorach T1, T2 oraz T3.
Wracaj─ůc do interpretacji wsp├│┼éczynnik├│w regresji:
- wsp├│┼éczynnik a zawsze jest r├│wny ┼Ťredniej dla grupy referencyjnej (tu a4) = 38,1
- wsp├│┼éczynnik bY1 jest r├│wny r├│┼╝nicy pomi─Ödzy ┼Ťredni─ů grupy, kt├│ra na wektorze T1 ma jedynki (tu a1) i ┼Ťredni─ů grupy referencyjnej (tu a4), czyli 20,7 ÔÇô 38,1 = - 17,4
- wsp├│┼éczynnik bY2 jest r├│wny r├│┼╝nicy pomi─Ödzy ┼Ťredni─ů grupy, kt├│ra na wektorze T2 ma jedynki (tu a2) i ┼Ťredni─ů grupy referencyjnej (tu a4), czyli 27,0 ÔÇô 38,1 = - 11,1
- wsp├│┼éczynnik bY3 jest r├│wny r├│┼╝nicy pomi─Ödzy ┼Ťredni─ů grupy, kt├│ra na wektorze T3 ma jedynki (tu a3) i ┼Ťredni─ů grupy referencyjnej (tu a4), czyli 28,5 ÔÇô 38,1 = - 9,6
Testy t zamieszczone w tabeli ÔÇ×Wsp├│┼éczynnikiÔÇŁ w wierszach dla ka┼╝dej z trzech zmiennych instrumentalnych testuj─ů po prostu, czy te r├│┼╝nice s─ů istotne statystycznie. I tak:
- r├│┼╝nica pomi─Ödzy grup─ů a1 i grup─ů a4 jest istotna statystycznie (t=-11,680; p<0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a2 i grup─ů a4 jest istotna statystycznie (t=-7,451; p<0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a3 i grup─ů a4 jest istotna statystycznie (t=-6,444; p<0,001)
Grupa referencyjna (a4) ma wi─Öc wy┼╝sz─ů ┼Ťredni─ů od wszystkich pozosta┼éych. Taki sam wynik uzyskali┼Ťmy w analizie wariancji.
4. Wyb├│r innej grupy jako grupy referencyjnej
Je┼╝eli wybierzemy inn─ů grup─Ö jako grup─Ö odniesienia, to zmieni si─Ö nam tylko (i to nie w ca┼éo┼Ťci) tabela ÔÇ×Wsp├│┼éczynnikiÔÇŁ.. Zakodujmy zmienn─ů jako┼Ťciow─ů raz jeszcze. Tym razem jednak zera na wszystkich zmiennych instrumentalnych przypiszmy grupie a3, za┼Ť jedynki na trzecim wektorze grupie a4. Efekt takiego kodowania zawiera poni┼╝sza tabela (wektory T1a, T2a i T3a).
|
|
Grupa |
czas |
T1 |
T2 |
T3 |
T1a |
T2a |
T3a |
|
1 |
1 |
21 |
1 |
0 |
0 |
1 |
0 |
0 |
|
2 |
1 |
23 |
1 |
0 |
0 |
1 |
0 |
0 |
|
3 |
1 |
21 |
1 |
0 |
0 |
1 |
0 |
0 |
|
4 |
1 |
15 |
1 |
0 |
0 |
1 |
0 |
0 |
|
5 |
1 |
20 |
1 |
0 |
0 |
1 |
0 |
0 |
|
6 |
1 |
25 |
1 |
0 |
0 |
1 |
0 |
0 |
|
7 |
1 |
27 |
1 |
0 |
0 |
1 |
0 |
0 |
|
8 |
1 |
16 |
1 |
0 |
0 |
1 |
0 |
0 |
|
9 |
1 |
22 |
1 |
0 |
0 |
1 |
0 |
0 |
|
10 |
1 |
17 |
1 |
0 |
0 |
1 |
0 |
0 |
|
11 |
2 |
30 |
0 |
1 |
0 |
0 |
1 |
0 |
|
12 |
2 |
29 |
0 |
1 |
0 |
0 |
1 |
0 |
|
13 |
2 |
21 |
0 |
1 |
0 |
0 |
1 |
0 |
|
14 |
2 |
22 |
0 |
1 |
0 |
0 |
1 |
0 |
|
15 |
2 |
31 |
0 |
1 |
0 |
0 |
1 |
0 |
|
16 |
2 |
28 |
0 |
1 |
0 |
0 |
1 |
0 |
|
17 |
2 |
26 |
0 |
1 |
0 |
0 |
1 |
0 |
|
18 |
2 |
25 |
0 |
1 |
0 |
0 |
1 |
0 |
|
19 |
2 |
27 |
0 |
1 |
0 |
0 |
1 |
0 |
|
20 |
2 |
31 |
0 |
1 |
0 |
0 |
1 |
0 |
|
21 |
3 |
33 |
0 |
0 |
1 |
0 |
0 |
0 |
|
22 |
3 |
28 |
0 |
0 |
1 |
0 |
0 |
0 |
|
23 |
3 |
29 |
0 |
0 |
1 |
0 |
0 |
0 |
|
24 |
3 |
33 |
0 |
0 |
1 |
0 |
0 |
0 |
|
25 |
3 |
30 |
0 |
0 |
1 |
0 |
0 |
0 |
|
26 |
3 |
27 |
0 |
0 |
1 |
0 |
0 |
0 |
|
27 |
3 |
25 |
0 |
0 |
1 |
0 |
0 |
0 |
|
28 |
3 |
29 |
0 |
0 |
1 |
0 |
0 |
0 |
|
29 |
3 |
25 |
0 |
0 |
1 |
0 |
0 |
0 |
|
30 |
3 |
26 |
0 |
0 |
1 |
0 |
0 |
0 |
|
31 |
4 |
42 |
0 |
0 |
0 |
0 |
0 |
1 |
|
32 |
4 |
32 |
0 |
0 |
0 |
0 |
0 |
1 |
|
33 |
4 |
39 |
0 |
0 |
0 |
0 |
0 |
1 |
|
34 |
4 |
35 |
0 |
0 |
0 |
0 |
0 |
1 |
|
35 |
4 |
41 |
0 |
0 |
0 |
0 |
0 |
1 |
|
36 |
4 |
38 |
0 |
0 |
0 |
0 |
0 |
1 |
|
37 |
4 |
37 |
0 |
0 |
0 |
0 |
0 |
1 |
|
38 |
4 |
40 |
0 |
0 |
0 |
0 |
0 |
1 |
|
39 |
4 |
39 |
0 |
0 |
0 |
0 |
0 |
1 |
|
40 |
4 |
38 |
0 |
0 |
0 |
0 |
0 |
1 |
Ni┼╝ej przedstawiono wydruk analizy regresji, w kt├│rej jako zmiennych niezale┼╝nych u┼╝yto wektor├│w T1a, T2a i T3a:
Regresja
Zmienne wprowadzone/usuni─Öte(b)
|
Model |
Zmienne wprowadzone |
Zmienne usuni─Öte |
Metoda |
|
1 |
T3a - (1) grupa a4, T2a - (1) grupa a2, T1a - (1) grupa a1(a) |
. |
Wprowadzanie |
a Wszystkie wyspecyfikowane zmienne zostały wprowadzone.
b Zmienna zale┼╝na: czas (zm. zale┼╝na)
Model - Podsumowanie
|
Model |
R |
R-kwadrat |
Skorygowane R-kwadrat |
B┼é─ůd standardowy oszacowania |
|
1 |
,892(a) |
,795 |
,778 |
3,33125 |
a Predyktory: (Stała), T3a - (1) grupa a4, T2a - (1) grupa a2, T1a - (1) grupa a1
Analiza wariancji(b)
|
Model |
|
Suma kwadrat├│w |
df |
Średni kwadrat |
F |
Istotno┼Ť─ç |
|
1 |
Regresja |
1552,275 |
3 |
517,425 |
46,627 |
,000(a) |
|
Reszta |
399,500 |
36 |
11,097 |
|
|
|
|
Ogółem |
1951,775 |
39 |
|
|
|
a Predyktory: (Stała), T3a - (1) grupa a4, T2a - (1) grupa a2, T1a - (1) grupa a1
b Zmienna zale┼╝na: czas (zm. zale┼╝na)
Współczynniki(a)
|
Model |
|
Współczynniki niestandaryzowane |
Współczynniki standaryzowane |
t |
Istotno┼Ť─ç |
|
|
B |
B┼é─ůd standardowy |
Beta |
||||
|
1 |
(Stała) |
28,500 |
1,053 |
|
27,054 |
,000 |
|
T1a - (1) grupa a1 |
-7,800 |
1,490 |
-,484 |
-5,236 |
,000 |
|
|
T2a - (1) grupa a2 |
-1,500 |
1,490 |
-,093 |
-1,007 |
,321 |
|
|
T3a - (1) grupa a4 |
9,600 |
1,490 |
,595 |
6,444 |
,000 |
|
a Zmienna zale┼╝na: czas (zm. zale┼╝na)
Nasze równanie będzie teraz miało postać:
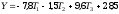
- wsp├│┼éczynnik a jest r├│wny ┼Ťredniej dla grupy referencyjnej (tu a3) = 28,5
- wsp├│┼éczynnik bY1 jest r├│wny r├│┼╝nicy pomi─Ödzy ┼Ťredni─ů grupy, kt├│ra na wektorze T1a ma jedynki (tu a1) i ┼Ťredni─ů grupy referencyjnej (tu a3), czyli 20,7 ÔÇô 28,5 = - 7,8
- wsp├│┼éczynnik bY2 jest r├│wny r├│┼╝nicy pomi─Ödzy ┼Ťredni─ů grupy, kt├│ra na wektorze T2a ma jedynki (tu a2) i ┼Ťredni─ů grupy referencyjnej (tu a3), czyli 27,0 ÔÇô 28,5 = - 1,5
- wsp├│┼éczynnik bY3 jest r├│wny r├│┼╝nicy pomi─Ödzy ┼Ťredni─ů grupy, kt├│ra na wektorze T3a ma jedynki (tu a4) i ┼Ťredni─ů grupy referencyjnej (tu a3), czyli 38,1 ÔÇô 28,5 = 9,6
I interpretacja test├│w t:
- r├│┼╝nica pomi─Ödzy grup─ů a1 i grup─ů a3 jest istotna statystycznie (t=-5,236; p<0,001)
- r├│┼╝nica pomi─Ödzy grup─ů a2 i grup─ů a3 nie jest istotna statystycznie (t=-1,007; p=0,321)
- r├│┼╝nica pomi─Ödzy grup─ů a4 i grup─ů a3 jest istotna statystycznie (t=-6,444; p<0,001)
Grupa referencyjna (a3) ma wi─Öc wy┼╝sz─ů ┼Ťredni─ů od a1, ni┼╝sz─ů od a4 i nie r├│┼╝ni si─Ö od a2. Taki sam wynik uzyskali┼Ťmy w analizie wariancji.
B. KODOWANIE QUASI-EKSPERYMENTALNE
1. Kodowanie quasi-eksperymantalne zmiennej jako┼Ťciowej
Profesor Brzezi┼äski pisze te┼╝ ┼╝e(s. 379)3: ÔÇ×Czytelnik, kt├│ry opanowa┼é ju┼╝ zasady kodowania zero-jedynkowego, bez trudu poradzi sobie z kodowaniem quasi-eksperymentalnym. R├│┼╝nica mi─Ödzy obydwoma systemami kodowania ÔÇô w sensie technicznym ÔÇô sprowadza si─Ö do tego, ┼╝e w kodowaniu zero-jedynkowym osobom z ostatniej grupy (p-tej) przypisano we wszystkich m wektorach instrumentalnych same zera, natomiast w kodowaniu tu omawianym miejsce zer zajmuj─ů wsp├│┼éczynniki ÔÇ×ÔÇô1.ÔÇŁ
Dla naszych danych oznacza to, ┼╝e dla czterech kategorii zmiennej niezale┼╝nej (cztery grupy os├│b badanych) b─Ödziemy musieli znowu utworzy─ç trzy wektory instrumentalne (T1, T2 i T3). Teraz jednak
- osoby z grupy a1 na wektorze T1 b─Öd─ů mia┼éy jedynki, a na pozosta┼éych wektorach zera (T1=1 T2=0 i T3=0)
- osoby z grupy a2 na wektorze T2 b─Öd─ů mia┼éy jedynki, a na pozosta┼éych wektorach zera (T1=0 T2=1 i T3=0)
- osoby z grupy a3 na wektorze T3 b─Öd─ů mia┼éy jedynki, a na pozosta┼éych wektorach zera (T1=0 T2=0 i T3=1)
- ale osoby z grupy a4 na wszystkich trzech wektorach b─Öd─ů mia┼éy nie zera, ale warto┼Ťci ÔÇô1 (T1=ÔÇô1 T2=ÔÇô1 i T3=ÔÇô1)
I tu znowu wszystkie grupy (tym razem jednak za wyj─ůtkiem ostatniej) b─Öd─ů odr├│┼╝nialne jedynie wtedy, gdy we┼║miemy pod uwag─Ö wszystkie trzy zmienne instrumentalne r├│wnocze┼Ťnie:
- grupa a1 ÔÇô sekwencja 1 0 0
- grupa a2 ÔÇô sekwencja 0 1 0
- grupa a3 ÔÇô sekwencja 0 0 1
- grupa a4 ÔÇô sekwencja ÔÇô1 ÔÇô1 ÔÇô1
Aby zakodowa─ç nasz─ů zmienn─ů jako┼Ťciow─ů w systemie quasi-eksperymentalnym prze─çwiczymy inny, alternatywny spos├│b tworzenia zmiennych instrumentalnych w pakiecie SPSS. Tym razem pos┼éu┼╝ymy si─Ö opcj─ů Rekoduj zmienne. W menu nale┼╝y wybra─ç nast─Öpuj─ůce polecenia:
1. Najpierw tworzymy pierwsz─ů zmienn─ů instrumentaln─ů (T1) na kt├│rej grupa a1 ma ÔÇ×1ÔÇŁ, grupa a4 ma ÔÇ×ÔÇô1ÔÇŁ, za┼Ť reszta ÔÇ×0ÔÇŁ.
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Rekoduj Ôćĺ Na inne zmienneÔÇŽ
- do okienka Zmienna ┼║rod┼éowa Ôćĺ wynikowa: przenosimy z obok wydrukowanej listy zmienn─ů ÔÇ×grupaÔÇŁ, a do okienka zatytu┼éowanego Zmienna wynikowa wpisujemy nazw─Ö nowego wektora: ÔÇ×T1ÔÇŁ i naciskamy przycisk Zmie┼ä. W wyniku tej operacji w okienku Zmienna ┼║r├│d┼éowa Ôćĺ wynikowa: pojawi si─Ö wpis: ÔÇ×grupa Ôćĺ T1ÔÇŁ. Oznacza on, ┼╝e cztery r├│┼╝ne warto┼Ťci wpisanej do pliku zmiennej ÔÇ×grupaÔÇŁ zostan─ů przekodowane na warto┼Ťci na nowo utworzonej zmiennej o nazwie T1.
- nast─Öpnie naciskamy przycisk Warto┼Ťci ┼║r├│d┼éowe i wynikowe i pojawia si─Ö tabela, kt├│ra podzielona jest na dwie cz─Ö┼Ťci zatytu┼éowane: Warto┼Ť─ç ┼║r├│d┼éowa oraz Warto┼Ť─ç wynikowa
- do okienka zatytu┼éowanego Warto┼Ť─ç po stronie Warto┼Ť─ç ┼║r├│d┼éowa wpisujemy liczb─Ö ÔÇ×1ÔÇŁ, i do okienka o tej samej nazwie po stronie Warto┼Ť─ç wynikowa wpisujemy liczb─Ö ÔÇ×1ÔÇŁ i naciskamy przycisk Dodaj. W wyniku tej operacji w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa pojawi si─Ö wpis ÔÇ×1 Ôćĺ 1ÔÇŁ. Oznacza on, ┼╝e wszystkie osoby z grupy a1 (oznaczone w zmiennej ÔÇ×grupaÔÇŁ liczb─ů 1) w wektorze T1 b─Öd─ů mia┼éy jedynki.
- do okienka zatytu┼éowanego Warto┼Ť─ç po stronie Warto┼Ť─ç ┼║r├│d┼éowa wpisujemy teraz liczb─Ö ÔÇ×2ÔÇŁ, a do okienka o tej samej nazwie po stronie Warto┼Ť─ç wynikowa wpisujemy liczb─Ö ÔÇ×0ÔÇŁ i naciskamy przycisk Dodaj. W wyniku tej operacji w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa pojawi si─Ö kolejny wpis: ÔÇ×2 Ôćĺ 0ÔÇŁ. Oznacza on, ┼╝e wszystkie osoby z grupy a2 (oznaczone w zmiennej ÔÇ×grupaÔÇŁ liczb─ů 2) w wektorze T1 b─Öd─ů mia┼éy zera.
- z kolei do okienka zatytu┼éowanego Warto┼Ť─ç po stronie Warto┼Ť─ç ┼║r├│d┼éowa wpisujemy liczb─Ö ÔÇ×3ÔÇŁ, a do okienka o tej samej nazwie po stronie Warto┼Ť─ç wynikowa wpisujemy liczb─Ö ÔÇ×0ÔÇŁ i naciskamy przycisk Dodaj. W wyniku tej operacji w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa pojawi si─Ö trzeci wpis: ÔÇ×3 Ôćĺ 0ÔÇŁ. Oznacza on oczywi┼Ťcie, ┼╝e wszystkie osoby z grupy a3 (oznaczone w zmiennej ÔÇ×grupaÔÇŁ liczb─ů 3) w wektorze T1 r├│wnie┼╝ b─Öd─ů mia┼éy zera.
- na koniec do okienka zatytu┼éowanego Warto┼Ť─ç po stronie Warto┼Ť─ç ┼║r├│d┼éowa wpisujemy liczb─Ö ÔÇ×4ÔÇŁ, a do okienka o tej samej nazwie po stronie Warto┼Ť─ç wynikowa wpisujemy liczb─Ö ÔÇ×ÔÇô1ÔÇŁ i naciskamy przycisk Dodaj. W wyniku tej operacji w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa pojawi si─Ö ostatni wpis: ÔÇ×4 Ôćĺ ÔÇô1ÔÇŁ. Oznacza on, ┼╝e wszystkie osoby z grupy a4 (oznaczone w zmiennej ÔÇ×grupaÔÇŁ liczb─ů 4) w wektorze T1 b─Öd─ů mia┼éy wpisane warto┼Ťci ÔÇ×ÔÇô1ÔÇŁ.
- teraz naciskamy po kolei przyciski Dalej oraz OK
SPSS dopisze do pliku now─ů zmienn─ů o nazwie ÔÇ×T1ÔÇŁ i osobom z grupy a1 przypisze na niej jedynki, osobom z grupy a4 warto┼Ťci ÔÇ×ÔÇô1ÔÇŁ, za┼Ť osoby z grup a2 oraz a3 b─Öd─ů mia┼éy na tej zmiennej przypisane zera.
2. Nast─Öpnie tworzymy drug─ů zmienn─ů instrumentaln─ů (T2) na kt├│rej grupa a2 ma ÔÇ×1ÔÇŁ, grupa a4 ma ÔÇ×ÔÇô1ÔÇŁ, za┼Ť reszta ÔÇ×0ÔÇŁ.
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Rekoduj Ôćĺ Na inne zmienneÔÇŽ
- do okienka Zmienna ┼║rod┼éowa Ôćĺ wynikowa: znowu przenosimy z obok wydrukowanej listy zmienn─ů ÔÇ×grupaÔÇŁ, a do okienka zatytu┼éowanego Zmienna wynikowa wpisujemy nazw─Ö kolejnego wektora: ÔÇ×T2ÔÇŁ i naciskamy przycisk Zmie┼ä. W wyniku tej operacji w okienku Zmienna ┼║r├│d┼éowa Ôćĺ wynikowa: pojawi si─Ö wpis: ÔÇ×grupa Ôćĺ T2ÔÇŁ. Oznacza on, ┼╝e cztery r├│┼╝ne warto┼Ťci wpisanej do pliku zmiennej ÔÇ×grupaÔÇŁ zostan─ů przekodowane na warto┼Ťci drugiej zmiennej instrumentalnej o nazwie T2.
- naciskamy przycisk Warto┼Ťci ┼║r├│d┼éowe i wynikowe i w tabeli, kt├│ra pojawi si─Ö w wyniku wybrania tej opcji wpisujemy kolejno do okienka Warto┼Ť─ç w cz─Ö┼Ťciach zatytu┼éowanych: Warto┼Ť─ç ┼║r├│d┼éowa oraz Warto┼Ť─ç wynikowa:
- liczby ÔÇ×1ÔÇŁ i ÔÇ×0ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×1 Ôćĺ 0ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a1 w wektorze T2 b─Öd─ů mia┼éy zera.
- liczby ÔÇ×2ÔÇŁ i ÔÇ×1ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×2 Ôćĺ 1ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a2 w wektorze T2 b─Öd─ů mia┼éy jedynki.
- liczby ÔÇ×3ÔÇŁ i ÔÇ×0ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×3 Ôćĺ 0ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a3 w wektorze T2 b─Öd─ů mia┼éy zera.
- liczby ÔÇ×4ÔÇŁ i ÔÇ×ÔÇô1ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×4 Ôćĺ ÔÇô1ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a4 w wektorze T2 b─Öd─ů mia┼éy wpisane warto┼Ťci ÔÇô1.
Po naci┼Ťni─Öciu przycisk├│w Dalej oraz OK. SPSS dopisze do pliku now─ů zmienn─ů o nazwie ÔÇ×T2ÔÇŁ i osobom z grupy a2 przypisze na niej jedynki, osobom z grupy a4 warto┼Ťci ÔÇ×ÔÇô1ÔÇŁ, za┼Ť osoby z grup a1 oraz a3 b─Öd─ů mia┼éy na tej zmiennej przypisane zera.
3. Teraz tworzymy trzeci─ů zmienn─ů instrumentaln─ů (T3) na kt├│rej grupa a3 ma ÔÇ×1ÔÇŁ, grupa a4 ma ÔÇ×ÔÇô1ÔÇŁ, za┼Ť reszta ÔÇ×0ÔÇŁ.
- Analiza Ôćĺ Przekszta┼écenia Ôćĺ Rekoduj Ôćĺ Na inne zmienneÔÇŽ
- i znowu do okienka Zmienna ┼║rod┼éowa Ôćĺ wynikowa: znowu przenosimy z obok wydrukowanej listy zmienn─ů ÔÇ×grupaÔÇŁ, a do okienka zatytu┼éowanego Zmienna wynikowa wpisujemy nazw─Ö ostatniego wektora instrumentalnego: ÔÇ×T3ÔÇŁ i naciskamy przycisk Zmie┼ä. W wyniku tej operacji w okienku Zmienna ┼║r├│d┼éowa Ôćĺ wynikowa: pojawi si─Ö wpis: ÔÇ×grupa Ôćĺ T3ÔÇŁ. Oznacza on, ┼╝e cztery r├│┼╝ne warto┼Ťci wpisanej do pliku zmiennej ÔÇ×grupaÔÇŁ zostan─ů przekodowane na warto┼Ťci drugiej zmiennej instrumentalnej o nazwie T3.
- post─Öpuj─ůc analogicznie do sposobu opisanego w dw├│ch wy┼╝ej opisanych punktach naciskamy przycisk Warto┼Ťci ┼║r├│d┼éowe i wynikowe i wpisujemy kolejno do okienek Warto┼Ť─ç w cz─Ö┼Ťciach zatytu┼éowanych: Warto┼Ť─ç ┼║r├│d┼éowa oraz Warto┼Ť─ç wynikowa:
- liczby ÔÇ×1ÔÇŁ i ÔÇ×0ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×1 Ôćĺ 0ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a1 w wektorze T3 b─Öd─ů mia┼éy zera.
- liczby ÔÇ×2ÔÇŁ i ÔÇ×0ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×2 Ôćĺ 0ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a2 w wektorze T3 b─Öd─ů mia┼éy zera.
- liczby ÔÇ×3ÔÇŁ i ÔÇ×1ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×3 Ôćĺ 1ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a3 w wektorze T3 b─Öd─ů mia┼éy jedynki.
- liczby ÔÇ×4ÔÇŁ i ÔÇ×ÔÇô1ÔÇŁ i naciskamy przycisk Dodaj. Wpis ÔÇ×4 Ôćĺ ÔÇô1ÔÇŁ w okienku ┼╣r├│d┼éowa Ôćĺ Wynikowa oznacza, ┼╝e wszystkie osoby z grupy a4 w wektorze T3 b─Öd─ů mia┼éy wpisane warto┼Ťci ÔÇô1.
Po naci┼Ťni─Öciu przycisk├│w Dalej oraz OK. SPSS dopisze do pliku now─ů zmienn─ů o nazwie ÔÇ×T3ÔÇŁ i osobom z grupy a3 przypisze na niej jedynki, osobom z grupy a4 warto┼Ťci ÔÇ×ÔÇô1ÔÇŁ, za┼Ť osoby z grup a1 oraz a3 b─Öd─ů mia┼éy na tej zmiennej przypisane zera.
Efekt wyżej przedstawionych przekształceń ilustruje poniższa tabela:
|
|
Grupa |
czas |
T1 |
T2 |
T3 |
|
1 |
1 |
21 |
1 |
0 |
0 |
|
2 |
1 |
23 |
1 |
0 |
0 |
|
3 |
1 |
21 |
1 |
0 |
0 |
|
4 |
1 |
15 |
1 |
0 |
0 |
|
5 |
1 |
20 |
1 |
0 |
0 |
|
6 |
1 |
25 |
1 |
0 |
0 |
|
7 |
1 |
27 |
1 |
0 |
0 |
|
8 |
1 |
16 |
1 |
0 |
0 |
|
9 |
1 |
22 |
1 |
0 |
0 |
|
10 |
1 |
17 |
1 |
0 |
0 |
|
11 |
2 |
30 |
0 |
1 |
0 |
|
12 |
2 |
29 |
0 |
1 |
0 |
|
13 |
2 |
21 |
0 |
1 |
0 |
|
14 |
2 |
22 |
0 |
1 |
0 |
|
15 |
2 |
31 |
0 |
1 |
0 |
|
16 |
2 |
28 |
0 |
1 |
0 |
|
17 |
2 |
26 |
0 |
1 |
0 |
|
18 |
2 |
25 |
0 |
1 |
0 |
|
19 |
2 |
27 |
0 |
1 |
0 |
|
20 |
2 |
31 |
0 |
1 |
0 |
|
21 |
3 |
33 |
0 |
0 |
1 |
|
22 |
3 |
28 |
0 |
0 |
1 |
|
23 |
3 |
29 |
0 |
0 |
1 |
|
24 |
3 |
33 |
0 |
0 |
1 |
|
25 |
3 |
30 |
0 |
0 |
1 |
|
26 |
3 |
27 |
0 |
0 |
1 |
|
27 |
3 |
25 |
0 |
0 |
1 |
|
28 |
3 |
29 |
0 |
0 |
1 |
|
29 |
3 |
25 |
0 |
0 |
1 |
|
30 |
3 |
26 |
0 |
0 |
1 |
|
31 |
4 |
42 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
32 |
4 |
32 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
33 |
4 |
39 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
34 |
4 |
35 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
35 |
4 |
41 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
36 |
4 |
38 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
37 |
4 |
37 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
38 |
4 |
40 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
39 |
4 |
39 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
|
40 |
4 |
38 |
ÔÇô1 |
ÔÇô1 |
ÔÇô1 |
2. Uruchomienie analizy regresji w pakiecie SPSS
Przypomnijmy, ┼╝e aby uruchomi─ç analiz─Ö regresji w pakiecie SPSS nale┼╝y ÔÇô jak ju┼╝ pokazywali┼Ťmy omawiaj─ůc kodowanie zero-jedynkowe - wybra─ç nast─Öpuj─ůce elementy z menu:
- Analiza Ôćĺ Regresja Ôćĺ LiniowaÔÇŽ
- do okienka Zmienna zale┼╝na przenosimy zmienn─ů ÔÇ×czasÔÇŁ
- do okienka Zmienne niezale┼╝ne przenosimy wektory instrumentalne ÔÇ×T1, T2 i T3ÔÇŁ
- upewnijmy si─Ö, ┼╝e w okienku Metoda znajduje si─Ö ÔÇ×Metoda wprowadzaniaÔÇŁ (zaznaczana domy┼Ťlnie)
Po klikni─Öciu przycisku OK otrzymamy nast─Öpuj─ůcy wydruk:
Regresja
Zmienne wprowadzone/usuni─Öte(b)
|
Model |
Zmienne wprowadzone |
Zmienne usuni─Öte |
Metoda |
|
1 |
T3, T2, T1(a) |
. |
Wprowadzanie |
a Wszystkie wyspecyfikowane zmienne zostały wprowadzone.
b Zmienna zale┼╝na: czas
Model - Podsumowanie
|
Model |
R |
R-kwadrat |
Skorygowane R-kwadrat |
B┼é─ůd standardowy oszacowania |
|
1 |
,892(a) |
,795 |
,778 |
3,33125 |
a Predyktory: (Stała), T3, T2, T1
Analiza wariancji(b)
|
Model |
|
Suma kwadrat├│w |
df |
Średni kwadrat |
F |
Istotno┼Ť─ç |
|
1 |
Regresja |
1552,275 |
3 |
517,425 |
46,627 |
,000(a) |
|
Reszta |
399,500 |
36 |
11,097 |
|
|
|
|
Ogółem |
1951,775 |
39 |
|
|
|
a Predyktory: (Stała), T3, T2, T1
b Zmienna zale┼╝na: czas
Współczynniki(a)
|
Model |
|
Współczynniki niestandaryzowane |
Współczynniki standaryzowane |
t |
Istotno┼Ť─ç |
|||
|
B |
B┼é─ůd standardowy |
Beta |
||||||
|
1 |
(Stała) |
28,575 |
,527 |
|
54,251 |
,000 |
||
|
T1 |
-7,875 |
,912 |
-,797 |
-8,632 |
,000 |
|||
|
T2 |
-1,575 |
,912 |
-,159 |
-1,726 |
,093 |
|||
|
T3 |
-,075 |
,912 |
-,008 |
-,082 |
,935 |
|||
a Zmienna zale┼╝na: czas
3. Interpretacja wydruku
Je┼╝eli por├│wnamy dwa wydruki:
dla analizy regresji z wykorzystaniem zmiennej jako┼Ťciowej zakodowanej w systemie zero-jedynkowym (punkt A2)
dla analizy regresji z wykorzystaniem zmiennej jako┼Ťciowej zakodowanej w systemie quasi-eksperymentalnym (punkt B2)
to oka┼╝e si─Ö, ┼╝e r├│┼╝ni─ů si─Ö one wy┼é─ůcznie warto┼Ťciami zamieszczonymi w ostatniej tabeli zatytu┼éowanej ÔÇ×Wsp├│┼éczynnikiÔÇŁ. St─ůd te┼╝ znaczenie i interpretacja warto┼Ťci wska┼║nika R-kwadrat oraz wyniku testu F s─ů w obu przypadkach identyczne (oraz zgodne z efektem analizy wariancji przeprowadzonej dla tych samych danych)
C├│┼╝ wi─Öc zmienia w interpretacji zale┼╝no┼Ťci pomi─Ödzy zmienn─ů zale┼╝n─ů (czas) oraz niezale┼╝n─ů zmienn─ů jako┼Ťciow─ů (grupa) zabieg kodowania quasi-eksperymentalnego? Ot├│┼╝ zmieni on interpretacj─Ö nadawan─ů cz─ůstkowym wsp├│┼éczynnikom a oraz b w r├│wnaniu regresji. Teraz przyjmie ono inn─ů ni┼╝ w przypadku kodowania zero-jedynkowego posta─ç:
- wz├│r og├│lny dla trzech wektor├│w instrumentalnych:
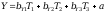
- r├│wnanie regresji dla zmiennej jako┼Ťciowej w systemie kodowania zero-jedynkowego (punkt A2 ÔÇô gdzie grupa a4 zakodowana zosta┼éa za pomoc─ů sekwencji: 0, 0, 0)

- r├│wnanie regresji dla zmiennej jako┼Ťciowej w systemie kodowania quasi-eksperymntalnego (punkt B2 ÔÇô gdzie grupa a4 zakodowana zosta┼éa za pomoc─ů sekwencji: ÔÇô1, ÔÇô1, ÔÇô1):
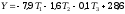
Równanie regresji policzone dla tych samych danych raz zakodowanych w systemie zero-jedynkowym, a raz w systemie quasi-eksperymentalnym zawiera inne współczynniki. Jak więc interpretować poszczególne współczynniki regresji z powyższego równania? Otóż:
- wsp├│┼éczynnik a to po prostu ┼Ťrednia og├│lna zmiennej zale┼╝nej (r├│wna 28,6)
- wsp├│┼éczynnik bY1 to odchylenie od ┼Ťredniej og├│lnej ┼Ťredniej tej grupy, kt├│ra na wektorze instrumentalnym T1 ma jedynki (20,7 ÔÇô 28,6 = ÔÇô 7,9)
- wsp├│┼éczynnik bY2 to odchylenie od ┼Ťredniej og├│lnej ┼Ťredniej tej grupy, kt├│ra ma jedynki na wektorze instrumentalnym T2 (27,0 ÔÇô 28,6 = ÔÇô 1,6)
- za┼Ť wsp├│┼éczynnik bY3 to odchylenie od ┼Ťredniej og├│lnej ┼Ťredniej tej grupy, kt├│ra z kolei na wektorze instrumentalnym T3 ma jedynki (28,5 ÔÇô 28,6 = ÔÇô 0,1).
Aby zrozumie─ç, co z tego wynika, wr├│─çmy na moment do modelu analizy wariancji.
3a. Raz jeszcze o analizie wariancji
Przypomnijmy, ┼╝e w jednoczynnikowej analizie wariancji struktur─Ö wyniku pojedynczej osoby badanej mo┼╝na wyrazi─ç w spos├│b nast─Öpuj─ůcy:
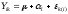
Co oznaczaj─ů kolejne symbole w wy┼╝ej przedstawionym r├│wnaniu? Ot├│┼╝:
Yik ÔÇô to wynik konkretnej osoby badanej (osoby k z grupy i). I tak na przyk┼éad wyra┼╝enie Y24 oznacza wynik 4-tej osoby z 2-giej grupy por├│wnawczej)
╬╝ ÔÇô ┼Ťredni wynik zmiennej Y w populacji
╬▒i ÔÇô efekt oddzia┼éywania i-tego poziomu czynnika A na zmienn─ů zale┼╝n─ů Y (i-ty poziom czynnika, to m├│wi─ůc inaczej grupa por├│wnawcza, do kt├│rej nale┼╝y osoba badana)
╬Ák(i) ÔÇô b┼é─ůd eksperymentalny (czyli zmienno┼Ť─ç Y wywo┼éana przez wszystkie te ┼║r├│d┼éa, kt├│re nie s─ů czynnikiem A)
Poniewa┼╝ m├│wimy tu o efektach populacyjnych (u┼╝ywamy greckiego alfabetu) powinni┼Ťmy si─Ö teraz zastanowi─ç nad tym, w jaki spos├│b s─ů one szacowane na podstawie warto┼Ťci uzyskanych w pr├│bie.
oszacowaniem ┼Ťredniej dla zmiennej zale┼╝nej w populacji (╬╝) jest ┼Ťrednia tej zmiennej w pr├│bie,
oszacowaniem efektu oddzia┼éywania i-tego poziomu czynnika A w populacji (╬▒i) jest odchylenie ┼Ťredniej odpowiadaj─ůcej i-temu poziomowi czynnika w pr├│bie od ┼Ťredniej og├│lnej w tej┼╝e pr├│bie (efekt b─Ödzie tym wi─Ökszy, im bardziej ┼Ťrednia grupowa b─Ödzie si─Ö r├│┼╝ni┼éa od ┼Ťredniej og├│lnej),
za┼Ť oszacowaniem efektu b┼é─Ödu eksperymentalnego w populacji (╬▒i) jest odchylenie wyniku osoby badanej od ┼Ťredniej odpowiadaj─ůcej i-temu poziomowi czynnika (tj. od ┼Ťredniej tej grupy, do kt├│rej nale┼╝y osoba badana).
Prze┼Ťled┼║my teraz kolejny przyk┼éad, kt├│ry pomo┼╝e w zrozumieniu to┼╝samo┼Ťci obu omawianych modeli.
|
grupa (czynnik) |
Średnia |
Odchylenie standardowe |
N |
|
a1 |
20,7000 |
3,86005 |
10 |
|
a2 |
27,0000 |
3,52767 |
10 |
|
a3 |
28,5000 |
2,91548 |
10 |
|
a4 |
38,1000 |
2,92309 |
10 |
|
Ogółem |
28,5750 |
7,07429 |
40 |
Wy┼╝ej zamieszczona tabela przypomina ┼Ťrednie dla ka┼╝dej z czterech grup eksperymentalnych oraz ┼Ťredni─ů dla ca┼éej pr├│by z┼éo┼╝onej z 40 os├│b badanych.
(1) Czas reakcji osoby numer 7 z pierwszej grupy por├│wnawczej (a1) wynosi 27 sek x 102 i mo┼╝emy go opisa─ç w nast─Öpuj─ůcy spos├│b:
|
Parametr populacyjny |
Oszacowanie parametru populacyjnego |
Obliczenia |
W przybli┼╝eniu |
|
╬╝ |
Średnia ogólna |
+ 28,575 |
+ 28,6 |
|
╬▒i |
┼Ürednia grupowa ÔÇô ┼Ťrednia og├│lna |
20,700 ÔÇô 28,575 = ÔÇô 7,875 |
ÔÇô 7,9 |
|
╬Ák(i) |
Wynik osoby badanej ÔÇô ┼Ťrednia grupowa |
27,000 ÔÇô 20,700 = + 6,300 |
+ 6,3 |
|
|
|
Suma (Y17) |
27,0 |
(2) Czas reakcji osoby numer 4 z drugiej grupy por├│wnawczej (a2) wynosi 22 sek x 102 i mo┼╝emy go opisa─ç tak::
|
Parametr populacyjny |
Oszacowanie parametru populacyjnego |
Obliczenia |
W przybli┼╝eniu |
|
╬╝ |
Średnia ogólna |
+ 28,575 |
+ 28,6 |
|
╬▒i |
┼Ürednia grupowa ÔÇô ┼Ťrednia og├│lna |
27,000 ÔÇô 28,575 = ÔÇô 1,575 |
ÔÇô 1,6 |
|
╬Ák(i) |
Wynik osoby badanej ÔÇô ┼Ťrednia grupowa |
22,000 ÔÇô 27,000 = ÔÇô 5,000 |
ÔÇô 5,0 |
|
|
|
Suma (Y24) |
22,0 |
(3) Czas reakcji osoby numer 9 z trzeciej grupy por├│wnawczej (a3) wynosi 25 sek x 102 i mo┼╝emy go opisa─ç nast─Öpuj─ůco::
|
Parametr populacyjny |
Oszacowanie parametru populacyjnego |
Obliczenia |
W przybli┼╝eniu |
|
╬╝ |
Średnia ogólna |
+ 28,575 |
+ 28,6 |
|
╬▒i |
┼Ürednia grupowa ÔÇô ┼Ťrednia og├│lna |
28,500 ÔÇô 28,575 = ÔÇô 0,075 |
ÔÇô 0,1 |
|
╬Ák(i) |
Wynik osoby badanej ÔÇô ┼Ťrednia grupowa |
25,000 ÔÇô 28,500 = ÔÇô 3,500 |
ÔÇô 3,5 |
|
|
|
Suma (Y39) |
25,0 |
(4) Czas reakcji osoby numer 1 z czwartej grupy por├│wnawczej (a4) wynosi 42 sek x 102 i mo┼╝emy go opisa─ç tak::
|
Parametr populacyjny |
Oszacowanie parametru Populacyjnego |
Obliczenia |
W przybli┼╝eniu |
|
╬╝ |
Średnia ogólna |
+ 28,575 |
+ 28,6 |
|
╬▒i |
┼Ürednia grupowa ÔÇô ┼Ťrednia og├│lna |
38,100 ÔÇô 28,575 = + 9,525 |
+ 9,5 |
|
╬Ák(i) |
Wynik osoby badanej ÔÇô ┼Ťrednia grupowa |
42,000 ÔÇô 38,100 = + 3,900 |
+ 3,9 |
|
|
|
Suma (Y41) |
42,0 |
3b. I znowu analiza regresji
Wr├│─çmy do r├│wnania regresji, kt├│re uzyskali┼Ťmy po zakodowaniu zmiennej jako┼Ťciowej w systemie quasi-eksperymentalnym (punkt B2):
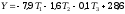
i odnie┼Ťmy je do wyr├│┼╝nionych pogrubion─ů czcionk─ů wierszy zawartych w tabelach [od (1) do (4)] w punkcie 3a:
ad (1) Efekt oddzia┼éywania i-tego poziomu czynnika dla osoby numer 7 z pierwszej grupy por├│wnawczej (a1) wynosi ÔÇô 7,9. Wsp├│┼éczynnik regresji bY1 dla wektora instrumentalnego T1 (na kt├│rym grupie a1 przypisano jedynki) r├│wnie┼╝ wynosi ÔÇô 7,9.
ad (2) Efekt oddzia┼éywania i-tego poziomu czynnika dla osoby numer 4 z drugiej grupy por├│wnawczej (a2) wynosi ÔÇô 1,6. Wsp├│┼éczynnik regresji bY2 dla wektora instrumentalnego T2 (na kt├│rym grupie a2 przypisano jedynki) r├│wnie┼╝ wynosi ÔÇô 1,6.
ad (3) Efekt oddzia┼éywania i-tego poziomu czynnika dla osoby numer 9 z trzeciej grupy por├│wnawczej (a3) wynosi ÔÇô 0,1. Wsp├│┼éczynnik regresji bY3 dla wektora instrumentalnego T3 (na kt├│rym grupie a3 przypisano jedynki) r├│wnie┼╝ wynosi ÔÇô 0,1.
ad (4) Efekt oddziaływania i-tego poziomu czynnika dla osoby numer 1 z czwartej grupy porównawczej (a4) wynosi + 9,5. Tego efektu nie znajdziemy wprost w równaniu regresji. Wrócimy do niego za moment.
Wszystko, co napisano powy┼╝ej mo┼╝na podsumowa─ç nast─Öpuj─ůco:
- wsp├│┼éczynniki zapisane przy kolejnych zmiennych instrumentalnych (od T1 do T3) w r├│wnaniu regresji s─ů to┼╝same z ocen─ů efekt├│w kolejnych poziom├│w czynnika (od a1 do a3) w modelu analizy wariancji.
Jak zatem w analizie regresji wyznaczy─ç efekt ostatniego poziomu czynnika (a4)? Musimy si─Ö tutaj odwo┼éa─ç do w┼éa┼Ťciwo┼Ťci ┼Ťredniej arytmetycznej. Kiedy w modelu analizy wariancji szukamy efekt├│w dzia┼éania poszczeg├│lnych poziom├│w czynnika, liczymy odchylenia kolejnych ┼Ťrednich grupowych od ┼Ťredniej og├│lnej (patrz tabele od 1 do 4 w punkcie 3a). Im wi─Öksze b─Öd─ů te odchylenia, tym wi─Ökszy efekt dzia┼éania czynnika. Jedn─ů z w┼éa┼Ťciwo┼Ťci ┼Ťredniej arytmetycznej jest ta, ┼╝e suma odchyle┼ä poszczeg├│lnych wynik├│w od tego wska┼║nika wynosi zero (poniewa┼╝ ┼Ťrednia arytmetyczna jest ┼Ťrodkiem ci─Ö┼╝ko┼Ťci dla wynik├│w, a co za tym idzie ÔÇô r├│wnowa┼╝y wszystkie warto┼Ťci, kt├│re s─ů od niej mniejsze oraz wi─Öksze). Dlatego tez suma efekt├│w wszystkich poziom├│w czynnika musi by─ç r├│wna zero. Dlatego te┼╝:
|
Efekt pierwszego poziomu czynnika |
╬▒1 |
r├│wna si─Ö ÔÇô 7,9 |
|
Efekt drugiego poziomu czynnika |
╬▒2 |
r├│wna si─Ö ÔÇô 1,6 |
|
Efekt trzeciego poziomu czynnika |
╬▒3 |
r├│wna si─Ö ÔÇô 0,1 |
|
Suma efekt├│w od ╬▒1 do ╬▒3 r├│wna si─Ö ÔÇô 9,6 |
||
Je┼╝eli (korzystaj─ůc z w┼éa┼Ťciwo┼Ťci ┼Ťrednie arytmetycznej) suma odchyle┼ä poszczeg├│lnych wynik├│w od ┼Ťredniej r├│wna si─Ö zero:
╬▒1 + ╬▒2 + ╬▒3 + ╬▒4 = 0
to:
╬▒4 = ÔÇô (╬▒1 + ╬▒2 + ╬▒3)
Dlatego:
╬▒4 = ÔÇô ( ÔÇô 7,9 ÔÇô 1,6 ÔÇô 0,1)
╬▒4 = + 9,6 [patrz tabela (4) punkt 3.a].
Oszacowali┼Ťmy w ten spos├│b efekt czwartego poziomu czynnika A (a4).
Na zako┼äczenie zapytajmy jeszcze o to, co oznacza test istotno┼Ťci poszczeg├│lnych wsp├│┼éczynnik├│w b w tabeli o nazwie ÔÇ×Wsp├│┼éczynnikiÔÇŁ (kt├│r─ů raz jeszcze przytaczamy poni┼╝ej) na wydruku z analizy regresji
Współczynniki(a)
|
Model |
|
Współczynniki niestandaryzowane |
Współczynniki standaryzowane |
t |
Istotno┼Ť─ç |
|||
|
B |
B┼é─ůd standardowy |
Beta |
||||||
|
1 |
(Stała) |
28,575 |
,527 |
|
54,251 |
,000 |
||
|
T1 |
-7,875 |
,912 |
-,797 |
-8,632 |
,000 |
|||
|
T2 |
-1,575 |
,912 |
-,159 |
-1,726 |
,093 |
|||
|
T3 |
-,075 |
,912 |
-,008 |
-,082 |
,935 |
|||
a Zmienna zale┼╝na: czas
Przypomnijmy, ┼╝e w przypadku kodowania zero-jedynkowego testy t zamieszczone w tej tabeli dla ka┼╝dej z trzech zmiennych instrumentalnych testuj─ů po prostu, czy r├│┼╝nica pomi─Ödzy ┼Ťrednim wynikiem dla tej grupy os├│b badanych, kt├│ra na danym wektorze instrumentalnym ma jedynki oraz ┼Ťrednim wynikiem grupy referencyjnej (zakodowanej za pomoc─ů sekwencji z┼éo┼╝onej z samych zer) jest istotna. Dzieje si─Ö tak, poniewa┼╝ kolejne wsp├│┼éczynniki b w r├│wnaniu regresji s─ů po prostu tymi r├│┼╝nicami.
W systemie kodowania quasi-eksperymentalnego wsp├│┼éczynniki b interpretowane s─ů inaczej. S─ů to odchylenia kolejnych ┼Ťrednich grupowych (poza ┼Ťredni─ů tej grupy, kt├│ra zakodowana zosta┼éa za pomoc─ů sekwencji z┼éo┼╝onej z warto┼Ťci ÔÇ×ÔÇô1ÔÇŁ) od ┼Ťredniej og├│lnej. Dlatego te┼╝ testy t zamieszczone w powy┼╝szej tabeli testuj─ů istotno┼Ť─ç takiego w┼éa┼Ťnie efektu. Okaza┼éo si─Ö, ┼╝e:
- ┼Ťrednia grupy a1 istotnie statystycznie r├│┼╝ni si─Ö od ┼Ťredniej og├│lnej (t= ÔÇô 8,632; p<0,001)
- ┼Ťrednia grupy a2 nie r├│┼╝ni si─Ö istotnie statystycznie od ┼Ťredniej og├│lnej (t= ÔÇô 1,726; p=0,093)
- ┼Ťrednia grupy a3 nie r├│┼╝ni si─Ö istotnie statystycznie od ┼Ťredniej og├│lnej (t= ÔÇô 0,082; p=0,935)
Ujemny znak przy wsp├│┼éczynnikach b (oraz oczywi┼Ťcie przy statystykach t) oznacza, ┼╝e wszystkie wy┼╝ej wymienione ┼Ťrednie grupowe s─ů ni┼╝sze od ┼Ťredniej og├│lnej. ┼Ürednia dla grupy a1 jest najni┼╝sza i istotnie r├│┼╝ni si─Ö od ┼Ťredniej og├│lnej. ┼Ürednie dla grup a2 oraz a3 s─ů wy┼╝sze od ┼Ťredniej grupy a1 (mniej si─Ö odchylaj─ů), od ┼Ťredniej og├│lnej si─Ö nie r├│┼╝ni─ů,
Gdyby┼Ťmy teraz zmienili spos├│b kodowania i inn─ů grup─Ö (a1, a2 lub a3) oznaczyliby┼Ťmy sekwencj─ů warto┼Ťci ÔÇ×ÔÇô1ÔÇŁ, to okaza┼éoby si─Ö, ┼╝e r├│┼╝nica pomi─Ödzy ┼Ťredni─ů grupy a4 i ┼Ťredni─ů og├│ln─ů jest istotna statystycznie, a wsp├│┼éczynnik b by┼éby dodatni. Oznacza to, ┼╝e wynik ten jest istotnie wy┼╝szy od ┼Ťredniej og├│lnej.
1 Brzeziński, J., Stachowski, R. (1984). Zastosowanie analizy wariancji w eksperymentalnych badaniach psychologicznych (wyd. 2). Warszawa: PWN.
2 Brzeziński, J. (1996). Metodologia badań psychologicznych. Warszawa: Wyd. Nauk. PWN.
3 Brzeziński, J. (1996). Metodologia badań psychologicznych. Warszawa: Wyd. Nauk. PWN.
Wyszukiwarka