Wrocław dn. 23.11.99.
LABORATORIUM FIZYKI OGÓLNEJ
SPRAWOZDANIE Z ĆWICZENIA NR 49
TEMAT: Zjawisko termoemisji elektronów
Wykonał Paweł Sokołowski
Wydz. Budownictwa Lądowego i Wodnego
Rok II
Gr.5
Wtorek 1415
Prowadzący dr T. Wiktorczyk
Wstęp
Celem ćwiczenia było wyznaczenie pracy wyjścia elektronów z wolframu oraz oraz pomiar charakterystyki prądowo-napięciowej diody próżniowej.
1.
Emisja elektronów z metalu (lub półprzewodnika)polega nauwalnianiu z jego powierzchni elektronówpod wpływem zewnętrznego czynnika pobudzającego. Takim czynnikiem może być wysoka temperatura,promieniowanie elektromagnetyczne, wysokie napięcie lub bombardujące cząstki.przedmiotem tego ćwiczenia byłobyło zbadanie termoemisji w diodzie próżniowej. Dioda jest najprostrzą lampą elektronową-jest to lampa dwu elektronowa.Jej elektrody(katoda i anoda) znajdują się w bańce szklanej, w której wytworzono wysoką prożnię.Aby wywołac termoemisje elektronów, ktodę diody podgrzewa się elektrycznie. Rozróżniasie się dwa rodzaje katod: zażonebezpośrednio i zażone pośrednio. W pierwszym przypadku katode stanowi cienki drucik metalowy,który zaży się w efekcie przepływającego prądu. Wdrugim przypadku katoda ma postać rurki metalowej, a grzejnik elektryczny jest umieszczony wewnątrz niej i od katody jest izolowany elektrycznie.
1.1.
Elektrony wewnątrz metalu można rozpatrywać jako cząstki znajdujące się w studni potencjału o skończonej wysokości.
Aby
elektron mógł opuścić metal musi pokonać barierę energetyczną
istniejącą na granicy metal-próżnia. Dla elektronów znajdujących
się na poziomie Fermiego wysokość tej bariery wynosi
 przy czym E
przy czym E jest
energia elektronu o energii kinetycznej równy zero, z dala od
powierzchni
metalu. Praca wyjścia
jest
energia elektronu o energii kinetycznej równy zero, z dala od
powierzchni
metalu. Praca wyjścia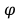 jest najmniejszą energią , jaką należy dostarczyć elektronowi
znajdującego się na poziomie Fermieg, aby mógł opuścić
powierzchnię metalu.
jest najmniejszą energią , jaką należy dostarczyć elektronowi
znajdującego się na poziomie Fermieg, aby mógł opuścić
powierzchnię metalu.
Aby elektron mógł opuścić powierzchnię metalu, składowa jego prędkości w kierunku prostopadłym do powierzchni katody musi spełniać warunek:

Zjawisko termoemisji ilościowej opisane zostało przez Richardsona i Dushmana równaniem:
I=A(1-R)sT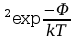
W którym:
A=4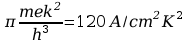
1.2.
Ruch elektronów w polu elektrycznym, charakterystyki prądowo-napięciowe diody. Na elektrony uwolnione z katody diody próżniowej działają następujące pola:
a)
Pole elektryczne między anodą i katodą pochodzące od zewnętrznego
napięcia przyłożonego do tych elektrod (napięcie anodowe U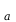 ).
Dla diody z płasko-równoległymi elektrodami pole to jest
jednorodne, a potencjał między katodą i anodą rośnie liniowo od
zera aż do potencjału anody V
).
Dla diody z płasko-równoległymi elektrodami pole to jest
jednorodne, a potencjał między katodą i anodą rośnie liniowo od
zera aż do potencjału anody V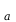 .
.
b)Pole pochodzące od chmury elektronów, które opuściły katodę i tworzą ładunek przestrzenny rozłożony w przestrzeni między katodą i anodą.Ten ładunek przestrzenny ujemnie naładowanej chmury elektronowej powoduje zaburzenia rozkładu potencjału między katodą i anodą. Aktualny potencjał jest więc w każdym punkcie przestrzeni niższy niż bez obecności ładunku przestrzennego.
c)
Pole elektryczne pochodzące od tzw. napięcia kontaktowego. Napięcie
kontaktowe powstaje wtedy ,gdy anoda i katoda wykonane są z
materiałów o różnych pracach wyjścia
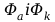 .
Napięcie kontaktowe jest wówczas określone równaniem :
.
Napięcie kontaktowe jest wówczas określone równaniem :
U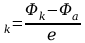
Jeśli
katoda i anoda diody próżniowej wykonane są z różnych
materiałów, wtedy rzeczywista wartość napięcia U między anodą
i katodą jest sumą algebraiczną napięcia anodowego U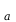 i
napięcia kontaktowego U
i
napięcia kontaktowego U
U=
U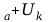
Obszar
prądu wybiegu występuje najczęściej dla ujemnych napięć
anodowych. Prąd ten powstaje w wyniku pokonywania przez najszybsze
elektrony niewielkiego pola hamującego istniejącego między katodą
i anodą. Gdy U


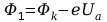
Podstawiając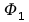 w miejsce
w miejsce
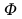 do
wzoru Richardsona otrzymujemy
do
wzoru Richardsona otrzymujemy
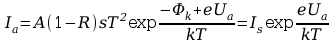
w
którym

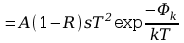
Jeśli
uwzględnimy napięcie kontaktowe między katodą i anoda , to do
wzoru w miejsce
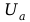 napięcie wypadkowe U wówczas:
napięcie wypadkowe U wówczas:
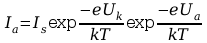
1.3. Wyznaczenie wykładnika potęgowego n (prawo Langmuira)
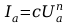

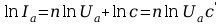
1.4. Wyznaczenie pracy wyjścia elektronów z katody metodą prostych Richardsona
Pracę wyjścia wyznacza się dla diody z katodą wolframową, mierząc zależność prądu termoemisji w funkcji temperatury katody
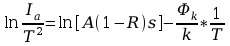
Jest
to równanie linii prostej we współrzędnych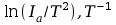
1.5.Wyznaczanie temperatury pracy katody wolframowej
Oporność
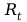 katody wolframowej w funkcji temperatury określona
jest przybliżonym wzorem:
katody wolframowej w funkcji temperatury określona
jest przybliżonym wzorem:
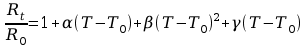
 -rezystancja
katody wolframowej w temperaturze pokojowej T
-rezystancja
katody wolframowej w temperaturze pokojowej T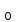 =293K
=293K
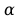 =(4,6
=(4,6
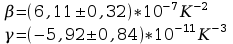
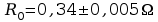 z
prawa Ohma otrzymujemy
z
prawa Ohma otrzymujemy
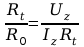
1.6. Charakterystyka prądowo - napięciowa
|
U |
I |
|
|
30,00 |
1,00 |
|
|
25,00 |
0,95 |
|
|
20,00 |
0,93 |
|
|
15,00 |
0,92 |
|
|
10,00 |
0,89 |
|
|
5,00 |
0,69 |
|
|
4,00 |
0,54 |
|
|
3,00 |
0,36 |
|
|
2,00 |
0,20 |
|
|
1,50 |
0,13 |
|
|
1,00 |
0,066 |
|
|
0,90 |
0,06 |
|
|
0,80 |
0,049 |
|
|
0,70 |
0,04 |
|
|
0,60 |
0,033 |
|
|
0,50 |
0,026 |
|
|
0,40 |
0,0205 |
|
|
0,30 |
0,016 |
|
|
0,20 |
0,012 |
|
|
0,10 |
0,0072 |
|
|
0,00 |
0,00 |
|
1.7. Badanie diody z katodą wolframową
|
I |
U |
I |
|
|
|
|
|
1 |
4,05 |
1,35 |
3,000 |
8,824 |
0,061 |
0,309 |
|
0,58 |
3,8 |
1,325 |
2,868 |
8,435 |
0,061 |
0,303 |
|
0,36 |
3,6 |
1,275 |
2,824 |
8,304 |
0,063 |
0,306 |
|
0,22 |
3,4 |
1,225 |
2,776 |
8,163 |
0,065 |
0,310 |
|
0,115 |
3,2 |
1,2 |
2,667 |
7,843 |
0,065 |
0,305 |
|
0,064 |
3,0 |
1,15 |
2,609 |
7,673 |
0,067 |
0,309 |
|
0,033 |
2,8 |
1,12 |
2,500 |
7,353 |
0,067 |
0,305 |
|
0,012 |
2,6 |
1,075 |
2,419 |
7,114 |
0,069 |
0,306 |
|
0,0058 |
2,4 |
1,04 |
2,308 |
6,787 |
0,069 |
0,304 |
|
0,002 |
2,2 |
0,95 |
2,316 |
6,811 |
0,076 |
0,324 |
|
0,00078 |
2,0 |
0,925 |
2,162 |
6,359 |
0,076 |
0,316 |
|
0,00022 |
1,8 |
0,875 |
2,057 |
6,050 |
0,078 |
0,319 |
|
0,00004 |
1,6 |
0,825 |
1,939 |
5,704 |
0,081 |
0,321 |
Przykłady obliczeń:
R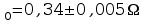

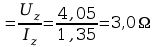
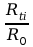 =
=
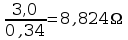
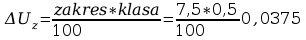 V
V
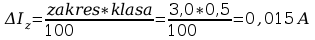
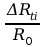 =
=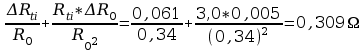
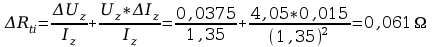
Wyszukiwarka