• Zadanie 18

Wzór na sumę n początkowych wyrazów ciągu arytmetycznego:

[A]

Dowód (indukcyjny):

1. dla n = 2 wzór jest prawdziwy, ponieważ:

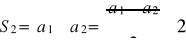
Załóżmy, że wzór na S_n jest prawdziwy dla pewnej liczby naturalnej n ( n  k -1, gdy ciąg jest k-wyrazowy) i rozważmy sumę S_n+1:

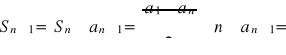
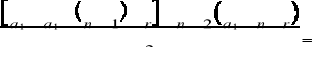
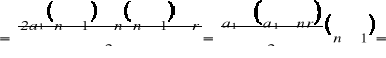
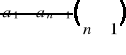
QED

Przykład:

Obliczyć sumę wszystkich liczb naturalnych od 1 do 1000.

Rozwiązanie:

Liczby 1, 2, 3,..., 1000 tworzą ciąg arytmetyczny, przy czym
, n = 1000,

Na podstawie wzoru [A] mamy:

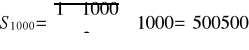
Odp. 500500.

Tutaj warto wspomnieć (za książką „Lilavati” Szczepana Jeleńskiego), że na pomysł takiego obliczania sumy liczb naturalnych wpadł podobno siedmioletni Karol Fryderyk Gauss (1777-1855), przyszły sławny matematyk niemiecki. Było to w pierwszej klasie szkoły początkowej.

Surowy nauczyciel, mając do przejrzenia prace uczniów ze starszych oddziałów, zwykł był dawać pierwszakom zadanie nieco trudniejsze, które musieli samodzielnie w milczeniu rozwiązywać. Umówiono się przy tym, że kto rozwiąże zadanie, ma odnieść zeszyt nauczycielowi i położyć na katedrze. Tym razem zadanie brzmiało: obliczyć sumę wszystkich liczb od 1 do 40. Ledwo nauczyciel zapisał zadanie na tablicy, zgłosił się do niego Karolek z gotowym rozwiązaniem. Nauczyciel myślał, że zadanie nie jest prawidłowo wyliczone. Jednak gdy już wszyscy uczniowie oddali zeszyty i nauczyciel je sprawdził, okazało się, że Gauss się nie pomylił.

A oto sposób rozumowania chłopca:

1, 2, 3, ... , 20

40, 39, 38, ... , 21

41, 41, 41, ... , 41

Najmniejsza i największa liczba dają w sumie 41, podobnie druga od początku liczba z drugą od końca itd. W wyniku tego spostrzeżenia Gauss pomnożył 41 razy 20 i wypisał jedyną liczbę wynikową: 820.

Zauważmy, że rozumowanie to prowadzi do zmodyfikowania wzoru [A] do postaci:

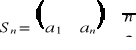
Przykład:

Obliczyć sumę wszystkich liczb nieparzystych od 1 do 99.

Rozwiązanie:

• Liczby 1, 3, ... , 99 tworzą ciąg arytmetyczny, przy czym
  , n = 50,
  , zatem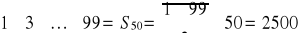
  

Odp.: 2500.

---