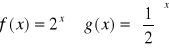Podać definicję odwzorowania odwrotnego.
Jaki warunek musi spełniać odwzorowanie, aby istniało dla niego odwzorowanie odwrotne?
Sformułować twierdzenie o składaniu odwzorowania danego i odwrotnego.
Podać określenie funkcji liczbowej jednej zmiennej. Czym ta definicja różni się od definicji odwzorowania?
Czy każda funkcja jest odwzorowaniem? Czy każde odwzorowanie jest funkcją?
Podać definicję ciągu liczbowego. Czym ta definicja różni się od definicji funkcji, odwzorowania?
Które z podanych odwzorowań jest ciągiem?
Podać przykład funkcji liniowej rosnącej i funkcji liniowej malejącej.
Podać przykład funkcji liniowej słaborosnącej.