Przykładowe pytania z matematyki dyskretnej

1. Co nazywamy drzewem?

2. Jakie grafy mają drzewo spinające?

3. Podaj warunek wystarczający na to, aby graf nieskierowany miał cykl Eulera.

4. Co nazywamy grafem spójnym?

5. Podaj warunek na to, by graf miał cykl Hamiltona.

6. Podaj warunek na to, aby krawędź e była częścią cyklu.

7. Co nazywamy izomorfizmem grafu G na graf H?

8. Podaj warunek na to, aby graf bez pętli i krawędzi wielokrotnych, mający n wierzchołków, był drzewem.

9. Jak wiążą się ze sobą stopnie wierzchołków grafu i liczba krawędzi? Objaśnij użyte symbole.

10. Podaj twierdzenie Eulera dla grafów skierowanych.

11. Co nazywamy drzewem spinającym?

12. Co nazywamy izomorfizmem grafu G na graf H?

13. Podaj twierdzenie o istnieniu ujścia i źródła w grafie skierowanym.

14. Co nazywamy cyklem?

15. Podaj warunek na to, by graf dwudzielny miał cykl Hamiltona.

16. Kiedy mówimy, że wierzchołek V jest osiągalny z wierzchołka U?

17. Podaj twierdzenie Eulera o grafach planarnych.

18. Co nazywamy ujściem grafu skierowanego?

19. Co wynika z tego, że istnieje droga z wierzchołka U do wierzchołka V?

20. Podaj twierdzenie o sumie stopni wierzchołków grafu.

21. Podaj warunek wystarczający na istnienie w grafie cyklu Hamiltona.

22. Co to jest drzewo spinające grafu? Kiedy istnieje?

23. Podaj warunek na to, aby graf acykliczny był drzewem. Jaki to warunek?

24. Podaj warunek na istnienie w grafie skierowanym cyklu Eulera.

25. Kiedy mówimy, że dwa grafy są izomorficzne?

26. Co to jest cykl?

27. Przy jakich założeniach wiemy, że w grafie G istnieje droga prosta acykliczna z wierzchołka U do wierzchołka V?

28. Kiedy dwa grafy nazywamy izomorficznymi?

29. Podaj warunek wystarczający na to, by graf miał cykl Eulera.

30. Jak brzmi uogólniona zasada indukcji?

31. Co nazywamy źródłem w grafie skierowanym?

32. Co wiemy o grafie dwudzielnym, jeśli ma on drogę Hamiltona?

33. Kiedy graf nazywamy pełnym?

34. Podaj warunki na to, by krawędź e należała do jakiegoś cyklu. Co to za warunki: konieczne czy wystarczające?

35. Jaki warunek musi spełniać graf mający cykl Eulera?

36. Co nazywamy drzewem binarnym?

37. Co wiemy o grafie dwudzielnym, jeśli ma on cykl Hamiltona?

38. Co nazywamy ujściem w grafie skierowanym?

39. Co nazywamy wysokością drzewa z wyróżnionym korzeniem?

40. Kiedy mówimy, że wierzchołek V jest osiągalny z wierzchołka U?

41. Przy jakich założeniach istnieje co najwyżej jedna droga prosta łącząca dwa wierzchołki grafu?

42. Ile krawędzi ma drzewo o n wierzchołkach?

43. Co to jest cykl Hamiltona?

44. Podaj przykład definicji rekurencyjnej.

45. Podaj twierdzenie Eulera dla grafów skierowanych.

46. Podaj związek między stopniami wierzchołków w grafie a liczbą krawędzi.

47. Co to jest graf dwudzielny?

48. Podaj warunki na to, by graf był drzewem. Co to za warunki: konieczne czy wystarczające?

49. Co nazywamy drzewem spinającym grafu?

50. Podaj warunek na to, by graf był hamiltonowski.

51. Podaj warunek na to, by graf miał drogę Eulera, ale nie miał cyklu Eulera.

52. Z czego składa się definicja rekurencyjna?

53. Podaj warunek na to, aby istniał cykl, do którego należy wierzchołek V.

54. Co nazywamy drogą w grafie skierowanym, a co długością drogi?

55. Kiedy graf nazywamy spójnym?

56. Co to jest droga Hamiltona w grafie?

57. Podaj warunek na to, by droga w grafie była acykliczna.

58. Kiedy możemy wnioskować, że krawędź w grafie należy do jakiegoś cyklu?

59. Co to jest stopień wierzchołka grafu?

60. Kiedy graf nazywamy drzewem?

61. Napisz prawo kontrapozycji w rachunku zdań.

62. Podaj twierdzenie o przedstawieniu formuły rachunku zdań w postaci koniunkcyjno - alternatywnej.

63. Napisz prawa de Morgana w algebrze Boole'a.

64. Co nazywamy funkcją logiczną?

65. Co to jest formuła w postaci alternatywno - koniunkcyjnej?

66. Napisz uogólnione prawa de Morgana w rachunku predykatów.

67. Kiedy zbiory nazywamy równolicznymi?

68. Narysuj układ bramek logicznych, który na wyjściu będzie dawał

69. Jak brzmi 1 Reguła Podstawiania?

70. Udowodnij za pomocą tablicy wartości logicznych, że

71. Co nazywamy funkcją logiczną?

72. Napisz prawa rozdzielności w algebrze Boole'a.

73. Co nazywamy pełnym zbiorem reszt modulo m?

74. Podaj twierdzenie o przedstawieniu
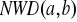
    za pomocą kombinacji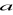
    i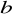
    .

75. Podaj własności relacji kongruencji.

76. Co nazywamy pełnym zbiorem reszt modulo m?

77. Jakie znamy własności funkcji Eulera?

78. Kiedy wiemy, że w w grupie istnieje permutacja nie mająca punktu stałego, tzn. przekształcająca każdy element tego zbioru na inny?

79. Co nazywamy G-orbitą w zbiorze X?

80. Ile wynosi liczba klas równoważnych kolorowań zbioru X?

81. Co to jest grupa?

82. Co nazywamy automorfizmem grafu skierowanego?

83. Ile jest orbit grupy G na zbiorze X?

84. Co nazywamy permutacją?

85. Podaj twierdzenie o ilości elementów (mocy) grupy G działającej na zbiorze X.

86. Jaką permutację nazywamy cyklem?

87. Co nazywamy siecią zdarzeń?

88. Kiedy mówimy, że grupa G jest generowana przez element g?

89. Jak grupa G działająca w zbiorze X dzieli ten zbiór?

90. Co nazywamy drogą krytyczną w grafie?

91. Czym charakteryzują się krawędzie leżące na drodze krytycznej?

92. Podaj sformułowanie zadania poszukiwania drogi maksymalnej w grafie.

93. Co nazywamy drogą krytyczną w grafie?

94. Kiedy rezerwa czasowa krawędzi (U,V) w sieci zdarzeń jest równa zero?

---