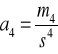Konstrukcja szeregu rozdzielczego z przedziałami klasowymi

1. Ustalenie liczby klas - k:

(gdzie n - liczba obserwacji)

2. Ustalenie rozpiętości przedziałów klasowych - h:

(gdzie R - rozstęp)

3. Ustalenie granic przedziałów klasowych - dolna granica pierwszego przedziału powinna obejmować najmniejszą wartość cechy
   .

Średnia arytmetyczna jest miarą położenia.

Informuje o przeciętnym poziomie badanej cechy w całej zbiorowości.

Wzór dla szeregu szczegółowego prostego:

Wzór dla szeregu szczegółowego ważonego:

Wzór dla szeregu rozdzielczego przedziałowego:

gdzie:

- średnia arytmetyczna

- i-ta wartość zmiennej X (i = 1, 2, ..., n)

n - liczba jednostek statystycznych badanej zbiorowości

f_i - liczba jednostek statystycznych odpowiadająca i-temu wariantowi zmiennej (n =
)

k - liczba wariantów zmiennej

środek przedziału klasowego

dolna granica przedziału

górna granica przedziału Modalna to wartość zmiennej, która występuje najczęściej w zbiorowości statystycznej.

gdzie:

x_m - dolna granica przedziału najbardziej licznego

f_m - liczebność przedziału modalnej

f_m-1 - liczebność przedziału poprzedzającego przedział modalnej

f_m+1 - liczebność przedziału następującego po przedziale modalnej

h - rozpiętość przedziału klasowego modalnej (interwał)

Kwantyle są to liczby spośród wartości cechy badanej zbiorowości, które dzielą ją na określone części pod względem liczby jednostek.

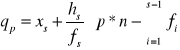
gdzie:

q_p - kwantyl rzędu p

x_s - dolna granica przedziału, w którym określony kwantyl się znajduje

h_s - interwał przedziału, w którym określony kwantyl się znajduje

f_s - liczebność przedziału, w którym określony kwantyl się znajduje

p - rząd kwantyla (0<p<1)

n - liczebność danej zbiorowości

- suma liczebności od 1 klasy do klasy poprzedzającej przedział kwantyla

Kwartyle - Q₁, Q₂, Q₃

Q₁ - kwartyl pierwszy dzieli zbiorowość uporządkowaną w ten sposób, że 25% jednostek ma wartości cechy nie wyższe, a 75% nie niższe niż Q_1.

Q₃ - kwartyl trzeci dzieli zbiorowość uporządkowaną w ten sposób, że 75% jednostek ma wartości cechy nie wyższe, a 25% nie niższe niż Q_3.

Q₂ - mediana (Me) - wartość środkowa

Jest to liczba, która dzieli szereg statystyczny na dwie równe części pod względem liczebności:

50% jednostek o wartościach większych lub równych medianie, a 50% o wartościach mniejszych lub równych.

Wariancja - średnia arytmetyczna z kwadratów odchyleń poszczególnych wartości cechy od ich średniej arytmetycznej. Jest to miara zmienności.

Wzór dla szeregu szczegółowego prostego:

Wzór dla szeregu szczegółowego ważonego:

Wzór dla szeregu rozdzielczego:

Odchylenie standardowe (s) informuje jaka jest średnia wartość odchyleń, a zatem o ile średnio jednostki danej zbiorowości różnią się od średniej arytmetycznej badanej zmiennej.

Współczynnik zmienności informuje o zróżnicowaniu wartości badanej zmiennej. Jest stosowany gdy zaistnieje potrzeba dokonania porównań zbiorowości ze względu na zmienność cech o różnych mianach (V>20% świadczy o znacznym rozproszeniu cechy).

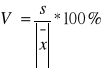
Współczynnik asymetrii jest miarą asymetrii.

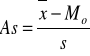
A_s = 0 to rozkład jest symetryczny

A_s > 0 to rozkład jest asymetryczny prawostronnie

A_s < 0 to rozkład jest asymetryczny lewostronnie

Im
jest większe, tym asymetria rozkładu jest silniejsza.

Inną miarą asymetrii jest moment centralny trzeciego rzędu

Wzór dla szeregu szczegółowego prostego:

Wzór dla szeregu rozdzielczego:

m₃ = 0 dla szeregów dokładnie symetrycznych

m₃ > 0 dla szeregów asymetrycznych prawostronnie

m₃ < 0 dla szeregów asymetrycznych lewostronnie

Współczynnik skośności (moment standaryzowany trzeciego rzędu - względna miara asymetrii)

Moment centralny czwartego rzędu jest miarą koncentracji (zbiorowości wokół wartości średniej).

Wzór dla szeregu szczegółowego prostego:

Wzór dla szeregu rozdzielczego:

Wskaźnik koncentracji (kurtoza - względna miara koncentracji)

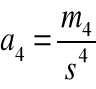
a₄ = 3 dla rozkładu normalnego

a₄ < 3 dla rozkładu spłaszczonego względem rozkładu normalnego

a₄ > 3 dla rozkładu wysmukłego względem rozkładu normalnego

Eksces

γ = 0 dla rozkładu normalnego

γ < 0 dla rozkładu spłaszczonego względem rozkładu normalnego

γ > 0 dla rozkładu wysmukłego względem rozkładu normalnego

2

---