Nr æw. 302	Data		Wydzia³ Elektryczny	Semestr III	Grupa I-1
Prowadz¹ca			Przygotowanie	Wykonanie	Ocena

Nr ćw. 206	Data 16.12.99	Paweł Szwec		Wydział Elektryczny		Semestr III		Grupa A-II
dr A. Skibiński				Przygotowanie		Wykonanie		Ocena

Temat: Wyznaczanie sta³ej siatki dyfrakcyjnej

1. Falowy charakter œwiat³a.

Œwiat³o jest fal¹ elektromagnetyczn¹ rozchodz¹c¹ siê w pró¿ni ze sta³¹ prêdkoœci¹ c. Jest rozchodz¹cym siê w przestrzeni zaburzeniem pola elektromagnetycznego. Do celów optycznych potrzebne jest jedynie opisanie w czasie wektora elektryczengo fali œwietlnej równaniem (dla fali biegn¹cej w kierunku osi x) :

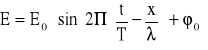
2. Zasada Hyghensa.

Jest ona oparta na konstrukcji geometrycznej i nie daje tak pe³nego obrazu jak elektromagnetyczna teoria Maxwella. Brzmi ona: ka¿dy punkt, który fala napotyka na swojej drodze staje siê Ÿród³em nowej fali kulistej; po³o¿enie fali mo¿na odczytaæ jako styczn¹ do fal cz¹stkowych. Jest to podstawa wyjaœnienia zjawisk dyfrakcji i interferencji.

3. Interferencja.

Jest to wzajemne nak³adanie siê fal. W okreœlonym punkcie przestrzeni nastapi wzmocnienie lub wygaszenie amplitudy w zale¿noœci od faz fal w tym punkcie.

a) Warunkiem na wygaszenie siê wzjamne dwóch fal jest odwrotnoœæ ich faz, czyli ró¿nica odleg³oœci od Ÿróde³ musi byæ równa po³owie wielokrotnoœci d³ugoœci fali.

b) Warunek zaœ konieczny do wygaszenia siê dwóch fal to zgodnoœæ ich faz, czyli ró¿nica odleg³oœci od ¿róde³ musi byæ równa ca³kowitej wielokrotnoœci d³ugoœci fali.

Chocia¿ interferencja zachodzi dla dowolnych fal to sta³y w czasie obraz interferncyjny mo¿na zaobserwowaæ jedynie dla Ÿróde³ spójnych (o sta³ej w czasie róznicy faz).

4. Dyfrakcja.

Jest to zjawisko ugiêcia siê fali zauwa¿alne, gdy przechodzi ona przez szczelinê o rozmiarach porównywalnych z d³ugoœci¹ fali.

dla jednej szczeliny:

dla dwóch szczelin:

5. Siatka dyfrakcyjna.

Jest to uk³ad szczelin wzajemnie równoleg³ych i le¿¹cych w sta³ej odleg³oœci. Wykonuje siê je przez naciêcie rowków na szkle lub metalowej p³ycie za pomoc¹ ostrza diamentowego. Maksimum g³ówne to obszar najwiêkszego podœwietlenia w œrodkowej czêœci widma ograniczony wyst¹pieniem pierwszego minimum lub wyst¹pieniem maksimów wtórnych, których natê¿enie jest bardzo ma³e. Jego szerokoœæ jest wyznaczona przez po³o¿enie pierwszego minimum, aopisana jest wzorem:

, gdzie:

W siatkach dyfrakcyjnych szerokoœæ szczelin jest rzêdu d³ugoœci fali œwietlnej, wiêc natê¿enie pr¹¿ków interferencyjnych jest prawie sta³e.

6. ZdolnoϾ rozdzielcza.

Siatka dyfrakcyjna ma zdolnoœæ rozdzielcz¹ R zdefiniowan¹ przez:

, gdzie:

jest œredni¹ d³ugoœci fali dwóch linii widmowych ledwie rozró¿nialnych, a jest ró¿nic¹ d³ugoœci fal miêdzy nimi.

7. Kryterium Rayleigh'a.

G³osi ono, ¿e dwa maksima s¹ ledwie rozró¿nialne, gdy ich odleg³oœæ k¹towa jest taka, ¿e maksimum jednej linii przypada na minimum drugiej. Jeœli zastosujemy to kryterium, to mo¿emy pokazaæ, ¿e :

R=Nm, gdzie:

R--zdolnoœæ rozdzielcza, N--ca³kowita liczba naciêæ, m--rz¹d obserwowanego widma.

8. Zasada pomiaru.

W celu znalezienia sta³ej siatki dyfrakcyjnej d (czyli odleg³oœci miêdzy œrodkami dwóch s¹siednich szczelin) skorzystamy z równania:

, gdzie:

n--rz¹d obserwowanego widma, --d³ugoœæ fali, --k¹t pod jakim obserwowane jest max. widma.

Wartoœci k¹tów dla poszczególnych rzêdów n odczytujemy za pomoc¹ spektrometru zaopatrzonego w dok³adn¹ podzia³kê k¹tow¹. Rozbie¿ne œwiat³o lampy sodowej wpada do kolimatora przez szczelinê umieszczon¹ w ognisku soczewki, przez co opuszcza go jako wi¹zka równoleg³a. Nastêpnie pada na siatkê dyfrakcyjn¹ zamontowan¹ na osi obrotu lunetki z soczewk¹ skupiaj¹c¹. Lunetka jest trwale po³aczona z k¹tomierzem, zatem jej po³o¿enie mo¿na z du¿¹ dok³adnoœci¹ odczytywaæ ze skali k¹towej zaopatrzonej w noniusz.

9. Wyniki pomiarów.

	Odchylenie pr¹¿ka rzêdu 1.		Odchylenie pr¹¿ka rzêdu 2.
L.p.	w lewo	w prawo	w lewo	w prawo
1	35320'	641'	34629'	1335'
2	35320,5'	640'	34632'	1336,5'
3	35319'	645'	34628'	1336'
4	35318,5'	640'	34631'	1335'
5	35318,5'	640,5'	34632'	1336'
6	35317'	645'	34632'	1335'
7	35318'	641,5'	34629'	1334,5'

=0,5'

10. Obliczenia i rachunek b³êdów.

Zgodnie z poleceniem w skrypcie obliczam wartoœæ sta³ej siatki dla ka¿dego z dokonanych

pomiarów (korzystaj¹c z wzoru w pkt. 8) otrzymuj¹c, po zaokr¹gleniu do 2 miejsc po przecinku nastêpuj¹ce wyniki :

	dla pr¹¿ka rzêdu 1.		dla pr¹¿ka rzêdu 2.
L.p.	w lewo	w prawo	w lewo	w prawo
1	5,0810-6	5,0710-6	5,0510-6	5,0210-6
2	5,0910-6	5,0810-6	5,0610-6	5,0110-6
3	5,0710-6	5,0210-6	5,0410-6	5,0110-6
4	5,0610-6	5,0810-6	5,0610-6	5,0210-6
5	5,0610-6	5,0710-6	5,0610-6	5,0110-6
6	5,0410-6	5,0210-6	5,0610-6	5,0210-6
7	5,0510-6	5,0610-6	5,0510-6	5,0210-6

Wartoœæ œrednia sta³ej siatki wynosi: 5,0510-6 m

11. Wnioski i uwagi.

Otrzymane wyniki pozwalaj¹ obliczyæ iloœæ rys przypadaj¹c¹ na cm dla badanej siatki. Wynosi ona oko³o 19800 rys/cm. Podsumowuj¹c, pomiary nie odbiega³y za bardzo od siebie za bardzo ze wzglêdu na zastosowanie noniusza przy mierzeniu k¹ta odchylenia, jednak przymocowanie lunetki pozostawia³o wiele do ¿yczenia.

W æwiczeniu mo¿na by u¿yæ kilka siatek i badaæ je pod kilkoma d³ugoœciami fali œwietlnej.

Sprawozdanie, str. 3