Sprawozdanie: Estymatory i ich własności Łukasz Przybyłek

Przemysław Stankiewicz

1. Przeanalizować zmienność rozkładu chi-kwadrat i T-Studenta z zależności od liczby stopni swobody.

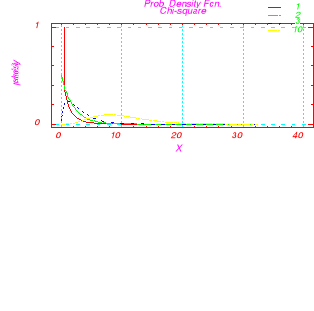
A. Wyznaczyć wykresy gęstości zmiennych losowych o rozkładzie chi-kwadrat z liczbą stopni swobody 1, 2, 3, 10.

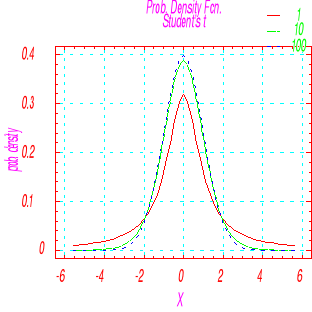
B. Wyznaczyć wykresy gęstości zmiennej losowej o rozkładzie T-studenta z liczbą stopni swobody 1, 10, 100.

2. Wygenerować próbkę o liczności 500 z rozkładem N(0, 1). Utworzyć z niej próbki o licznościach 10, 20, 30, 40, 50 ,100, 200, 300, 400, 500 z początkowych elementów danej próbki.

A. Wyznaczyć zbiory N, M, A, U, V gdzie:

N: wartość liczności próbek

M: mediany próbek

A: estymatory wartości oczekiwanej

U, V: dolne i górne krańce 90% przedziału ufności dla wartości oczekiwanej odpowiadające kolejnym próbkom.

Na wspólnym wykresie przeanalizować zależność powyższych statystyk od liczności próbek.

B. Wykonać to samo dla wariancji.

Jak zmieniłyby się wykresy dla prób z rozkładów N(0; 0.1), N(0, 10)?

1:

Wnioski:

Dla rozkładu chi-kwadrat dla małej liczby (1,2) stopni swobody wykresy funkcji gęstości są lewostronnie asymetryczne i w żadnym stopniu nie przypominają wykresów funkcji gęstości rozkładu normalnego. Wykresy są wysmukłe, co oznacza, że współczynnik spłaszczenia jest mniejszy od zera, a gęstość duża. Wraz ze wzrostem liczby stopni swobody, lewe „zbocze” wykresu zaczyna się uwidaczniać i zbiegać ku środkowi, co oznacza, że gęstość maleje, a wykres przesuwa się względem osi X, czyli zmienia się jego wartość oczekiwana. Zwiększając dalej liczbę stopni swobody wykres gęstości spłaszcza się . oraz można go z dużą dokładnością porównywać z rozkładem normalnym.

Dla rozkładu T-Studenta dla małej liczby (1) stopni swobody wykres funkcji gęstości jest w pewnym stopniu podobny (węższy) do wykresu funkcji gęstości rozkładu normalnego, gdyż stopień spłaszczenia tego wykresu jest większy od zera. Wraz ze wzrostem liczby stopni swobody, oba „zbocza” wykresu zaczynają się rozchodzić od środka, przez co wykres w większym stopniu zaczyna przypominać wykres funkcji gęstości rozkładu normalnego. Wykres gęstości jest symetryczny względem prostej x=0. W przypadku, gdy liczba stopni swobody jest duża wykres gęstości rozkładu T-Studenta można z powodzeniem porównywać z wykresem gęstości rozkładu normalnego.

2:

Liczność próbki (N)	Mediana (M)	Estymator wartości oczekiwanej (A)	90% przedział ufności dla wartości oczekiwanej		Estymator wariancji (A')	90% przedział ufności dla wariancji
							Dolna granica (U)	Górna granica (V)		Dolna granica (U')	Górna granica (V')
10	-0.2663131	-0.1457818	-0.5888913	0.2973276	0.7257174	0.4289369	2.182535
20	-0.2663131	-0.1041963	-0.4786588	0.2702662	1.036554	0.687746	2.049131
30	-0.2382595	-0.1375212	-0.4522875	0.177245	1.098609	0.7744504	1.861169
40	-0.1722427	-0.1974795	-0.4600634	0.06510441	1.019393	0.7272965	1.530577
50	-0.06661018	-0.1924157	-0.4179635	0.03313206	0.9401401	0.6933053	1.346742
100	-0.05925898	-0.09466371	-0.2530957	0.06376823	0.92775	0.744496	1.188037
200	-0.03742054	-0.01801514	-0.1319605	0.09593024	0.9597739	0.8194446	1.139497
300	-0.07684501	-0.02532087	-0.1178487	0.067207	0.9493182	0.8336047	1.090910
400	-0.05833931	-0.01039249	-0.0892423	0.06845732	0.9191932	0.820935	1.036209
500	-0.07096898	-0.03774812	-0.1096177	0.03412148	0.954566	0.8625062	1.062192

Wnioski:

Patrząc na tabelę wyników i sporządzone na jej podstawie wykresy, możemy wywnioskować, że wraz ze wzrostem liczności próbki przedziały ufności zawężają się. Górna granica przedziału ufności dla wariancji wykazuje stałą tendencję spadkową. Przedziały ufności zachowują się różnie dla różnych liczności próbki: raz rosną, raz maleją. Prawidłowość występuje w wartościach estymatorów: jeśli od górnej granicy przedziału ufności odejmiemy dolną, to w przybliżeniu dostaniemy estymator odpowiedniego parametru. Im większa liczność próbki, węższy przedział ufności, tym dokładniejsza wartość estymowanego parametru. Dla małych liczności próbki przedział ufności dla obu parametrów jest bardzo duży, a wartość estymowanych parametrów nie znajduje się w środku przedziału, czyli dokładność estymacji danego parametru jest mała. Uwagę zwraca też większa wartość mediany od wartości oczekiwanej przy dobrze widocznym spadku górnej granicy przedziału ufności.

Dla rozkładu N(0; 0.1) wykres jest węższy z powodu małego odchylenia standardowego.

Dla rozkładu N(0; 10) wykres jest szerszy z powodu dużego odchylenia standardowego.

2

---