Politechnika Śląska Gliwice 01.03.1999r.

Wydział Elektryczny

Kierunek EiT

Ćwiczenie laboratoryjne z fizyki

Badanie temperaturowej zależności współczynnika lepkości cieczy za pomocą wiskozymetru Höplera.

Grupa T2 sekcja I

Tomasz Hauser

Paweł Łoskot

1. Wprowadzenie.

Każde ciało poruszające się w cieczy czy gazie doznaje pewnej hamującej siły wskutek tego, że warstewki cieczy przylegające do ciała będącego w ruchu pociągają za sobą coraz dalsze warstewki sąsiednie. Podobnie jak w przypadku przepływu cieczy przez rurki kapilarne mamy tu do czynienia z przesuwaniem się jednych warstewek cieczy względem drugich. Istnieje spad prędkości cząsteczek cieczy w kierunku prostopadłym do kierunku ruchu.

Siła która wywołuje ten spad prędkości, ma swe źródło w przyciąganiu między cząsteczkowym. Jest ona czynnikiem hamującym ruch, przypisujemy jej zatem zwrot przeciwny kierunkowi ruchu i nazywamy ją tarciem wewnętrznym cieczy albo lepkością - w odróżnieniu od tarcia zewnętrznego, z którym mamy do czynienia wówczas, gdy dwie powierzchnie różnych ciał poruszają się względem siebie.

Prawo Stokesa, według którego gładka kulka o promieniu r, poruszająca się w cieczy ze stałą prędkością v doznaje oporu tarcia T skierowanego przeciwnie względem v, wyraża się wzorem:

Ft=-6pηrv.

Wielkość h jest niezależna od materiału, z którego wykonano kulkę, zależy natomiast od rodzaju cieczy i bardzo silnie od jej temperatury. Ruchy termiczne cząstek mają wpływ na siły oddziaływania między cząsteczkowego. W cieczach wzrost prędkości ruchów termicznych siły te osłabia, w gazach sytuacja jest odwrotna, ze wzrostem temperatury współczynnik lepkości wzrasta, gdyż przy wzroście temperatury rosną prędkości cząsteczek.

Wielkość η, stała dla danej cieczy i temperatury, nosi nazwę współczynnika lepkości lub tarcia wewnętrznego cieczy. Jeżeli kulka wykonana jest z materiału o gęstości ρ większej od gęstości ρp płynu, to ruch może następować na skutek działania siły ciężkości:

Ponieważ jednak kulka spada, w ośrodku płynnym działa na nią dodatkowo siła wyporu Fw, która zgodnie z prawem Archimedesa wyraża się wzorem:

Sumując wszystkie siły działające na kulkę otrzymamy:

F=Fg+Fw+Ft

czyli:

Siła Stokesa zależy od prędkości i istnieje taka prędkość vo, przy której siła F jest równa zeru, co oznacza, że kulka porusz się ruchem jednostajnym (I-szą zasada dynamiki). Jeżeli prędkość jest różna od vo, to kulka porusza się ruchem przyspieszonym i jej prędkość wzrasta lub maleje do chwili osiągnięcia wartości vo. Równanie: Ft=-6pηrv, stosuje się ściśle tylko w przypadku, gdy kulka porusz się w ośrodku o nieograniczonej szerokości i gdy mamy do czynienia z ruchem laminarnym. W przypadku, gdy kulka porusza się w rurze o promieniu rk, wypełnionej cieczą, wtedy równanie Stokesa przyjmuje postać:.

Uwzględniając tę poprawkę w równaniu na sumę sił działających na kulkę i zakładając F=0 oraz v=l/t, gdzie t jest czasem spadania kulki, otrzymujemy:

.

Spadek kulki w płynie ulega znacznemu zwolnieniu w rurce o średnicy nieznacznie przekraczającej średnicę kulki. Wtedy rurkę musimy ustawić nieco ukośnie, gdyż przy ustawieniu pionowym ruch kulki nie jest jednostajny. Przy ustawieniu skośnym kulka toczy się po ściance rurki. Do omawianego przypadku stosuje się wzór zapisany w postaci: η=K(ρk-ρo)t, gdzie K jest stałą przyrządu, którą wyznaczamy z pomiaru wykonanego dla płynu o znanym współczynniku lepkości. Współczynnik lepkości zależy w dużym stopniu od temperatury. Dla cieczy zależnością tą rządzi prawo:

gdzie T jest temperaturą w skali Kelvina, A i B - stałe charakteryzujące ciecz.

2. Przebieg ćwiczenia.

Zmieniając temperaturę cieczy przy pomocy ultra termostatu z termometrem kontaktowym, w granicach od temperatury pokojowej (26°C) do 50˚C co 3°C, mierzymy czas opadania kulki między skrajnymi położeniami obserwacyjnymi. Dla każdej temperatury pomiary powtarzamy trzykrotnie.

3. Tabele z wynikami pomiarów.

Lp.	Temperatura T[˚C]	Czas opadania kulki t[s]
				1	2	3	średnia
1.	26	159	163	162	161.3
2.	29	132	130	134	132.0
3.	32	113	111	112	112.0
4.	35	93	94	91	92.7
5.	38	78	80	78	78.7
6.	41	66	65	67	66.0
7.	44	56	57	55	56.0
8.	47	48	46	47	47.0

Dokładność pomiaru temperatury ΔT = 0.5 [˚C],

Dokładność pomiaru czasu Δt = 0.1 [s],

Stała aparaturowa K = 1.2018 ^. 10^-6 [m²/s²],

Gęstość kulki ρ_k = 8150 [kg/m³],

Stała Boltzmana k = 1.38 ^. 10^-23 [J/K].

Temperaturowa zależność gęstości oleju parafinowego.

Temperatura [˚C]	Gęstość oleju [kg/m^3]
20	878.8
25	875.3
30	871.8
35	868.3
40	864.8
45	861.2
50	857.5

Można zauważyć, że gęstość oleju zależy od temperatury liniowo. Po opracowaniu danych z tabeli i załączonego wykresu temperaturowej zależności gęstości oleju otrzymaliśmy wzór przedstawiający gęstość w funkcji temperatury, który posłuży do obliczenia gęstości oleju w temperaturach w których wykonywaliśmy pomiary:

4.Opracowanie pomiarów.

Dla każdej temperatury obliczamy współczynnik lepkości oleju parafinowego stosując wzór:

η=K(ρk-ρo)t,

Dla każdego η wyliczamy metodą różniczki zupełnej błąd dη ze wzoru:

dη = K(ρk-ρo)dt,

Następnie rysujemy wykres zależności temperaturowej współczynnika lepkości oleju parafinowego. Obliczamy kolejno ln|η|, oraz błąd. Dla kolejnych temperatur otrzymano:

lp.	T [°C]	ρ0		η [kg/ms]	dη [kg/ms]	ln|η| [kg/ms]	ln|dη| [kg/ms]
1	26	874.6	0.00334	1.41034	0.00087	0.34383	-7.04202
2	29	872.5	0.00331	1.15449	0.00087	0.14365	-7.04173
3	32	870.3	0.00328	0.97986	0.00087	-0.02035	-7.04143
4	35	868.3	0.00325	0.81123	0.00088	-0.20920	-7.04116
5	38	866.1	0.00321	0.68892	0.00088	-0.37263	-7.04085
6	41	864.0	0.00318	0.57792	0.00088	-0.54833	-7.04057
7	44	861.9	0.00315	0.49049	0.00088	-0.71234	-7.04028
8	47	859.8	0.00312	0.41178	0.00088	-0.88726	-7.03999

Temperaturowa zależność współczynnika lepkości jest opisana równaniem

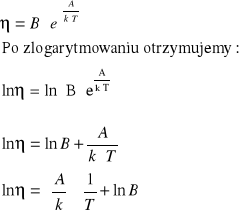
Otrzymujemy równanie liniowe postaci y =ax+b, można więc wyliczyć współczynniki A i B metodą regresji liniowej.

Po zastosowaniu programu wykonującego obliczenia otrzymano:

A = 7.53086 ^. 10^-20

B = 1.66730 ^. 10^-8

5. Wnioski.

W wyniku badania temperaturowej zależności współczynnika lepkości cieczy przy pomocy wiskozymetru Höplera otrzymano następujące wartości liczbowe współczynników:

A=7.53086 ^. 10^-20 [J],

B=1.66730 ^. 10^-8 [kg/ms],

które służą do wyliczenia współczynnika lepkości oleju parafinowego badanego podczas ćwiczenia. W wyniku porównania współczynnika lepkości wyliczonego ze wzoru η=K(ρk-ρo)t, ze współczynnikiem wyliczonym ze wzoru:

widać, że obydwie wartości pokrywają się.

Na podstawie wykresu obserwujemy, że charakterystyka temperaturowa współczynnika lepkości zależy od temperatury. Wraz ze wzrostem temperatury lepkość cieczy maleje.

Badanie temperaturowej zależności współczynnika lepkości cieczy za pomocą wiskozymetru Höplera

- 5 -

---