Politechnika Koszalińska

Wydział Budownictwa i Inżynierii Środowiska

Geodezja i Kartografia

Temat: Tyczenie prostych i prostopadłych. Bezpośredni pomiar odległości.

Termin wykonania laboratorium: 6.10.2011r.

Termin oddania sprawozdania: 20.10.2011r.

Termin oddania poprawy: 10.11.2011r.

Wykonał: Filip Stachniak

Grupa laboratoryjna: 5

1. Założenia teoretyczne:

Tyczenie prostej zadanej przez dwa utrwalone punkty skrajne A, B metodą bezpośredniego pomiaru odległości okiem nieuzbrojonym polega na wprowadzeniu pewnej liczby punktów pośrednich:

1, 2, 3, … na płaszczyznę pionową przechodzącą przez punkty A, B. W dostępnym terenie i przy bezpośredniej widoczności punktów końcowych A, B ustalenie położenia punktów pośrednich 1, 2, 3, … odbywa się poprzez obserwację wzrokową (wizowanie), podczas której obserwator, stojący w odległości 3-5m od punktu początkowego A, okiem nieuzbrojonym (tzw. na oko) patrzy na tyczki skrajne i korzystając z sygnałów dawanych rękoma, wskazuje pomocnikowi kierunek przesunięcia trzymanej przez niego tyczki aż do momentu uzyskania jej pokrycia się z tyczkami A, B. Najprostszym i najczęściej stosowanym sposobem bezpośredniego tyczenia prostej jest tyczenie w przód, czyli tyczenie poczynając od końca, tj. od punktu pośredniego położonego najdalej od stanowiska obserwatora, a kończąc na punkcie najbliższym. Odwrotny kierunek tyczenia spowodowałby zasłanianie tyczek dalszych przez wcześniej ustawione tyczki.

• Tyczenie w przód

Aby wyznaczyć prostą prostopadłą do odcinka AB, przechodzącą przez punkt P na tej prostej należy ustawić się z węgielnicą dwupryzmatyczną pentagonalną tak, aby pion znajdował się nad punktem P. Jedno okienko węgielnicy skierować w stronę tyczki A, drugie w stronę tyczki B, a następnie zgrać ich obrazy w pionie, obserwując przez trzecie okienko tyczkę C. Kierować pomiarowym z tyczką C do momentu, w którym stanie się ona przedłużeniem obrazów tyczek A i B w obu pryzmatach.

• Tyczenie prostopadłych za pomocą węgielnicy

2. Część praktyczna:

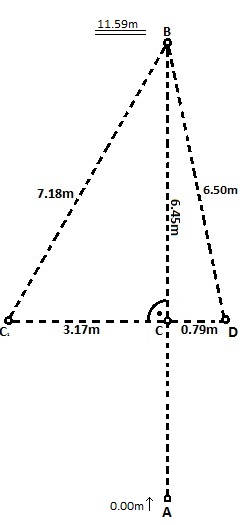
Pomiar „tam”: D₁ = 11.58m

Pomiar „z powrotem”: D₂ = 11.60m

Średnia z pomiarów: D _śr = 11.59m

Sprawdzenie dokładności pomiarów „tam” i „z powrotem”

ΔD_dop. = |D₂ - D₁|

ΔD_dop. = 0.004

ΔD_dop. ≤ 0.0059 * √D_śr

0.004 ˂ 0.06

Długość rzeczywista pomiaru:

a) |BC₁| = 7.18m

b) |BD| = 6.50m

Sprawdzenie dokładności pomiaru zgodnie z twierdzeniem Pitagoras'a o stosunku długości krawędzi w trójkącie prostokątnym (a² + b² = c²⁾, czyli:

a) |CC₁|² + |BC|² = |BC₁|²

|BC₁|² = 3.17² + 6.45² /^√

|BC₁|= 7.1869m

Błąd pomiaru: 7.1869 - 7.18 = 0.0069m

b) |BD|² = |BC|² + |CD|²

|BD|² = 6.45² + 0.79² /^√

|BD| = 6.4982m

Błąd pomiaru: 6.50 - 6.4982 = 0.0018m

Błędy pomiarów mieszczą się w normie, a więc pomiary są możliwie dokładne i akceptowalne.

3. Podsumowanie i wnioski:

Pomiary były możliwie dokładne jednak podczas wykonywania ćwiczenia mogło dojść do szeregu błędów pomiarowych, które dzielą się na:

1. błędy przypadkowe:

- błąd przyłożenia taśmy do punktu początkowego oraz do wszystkich tyczek pośrednich

- niedokładne umiejscowienie tyczek pośrednich

- błąd odczytu końcowego

- błąd spowodowany niejednakowym naciągiem taśmy

b) błędy systematyczne:

- poprawka kompilacyjna

c) błędy grube (omyłki):

- nieuwaga lub niedopatrzenie obserwatora/ osoby pomiarowej

---