Dodatkowo przy wykorzystaniu programu 7.4 rozwiązywano metodą siatek zagadnienie:
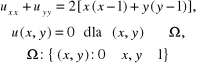
(7.135)
i porównywano z rozwiązaniem dokładnym
![]()
dla przetestowania szybkości zbieżności metody najszybszego spadku i metody sprzężonych gradientów.
PROGRAM 7.4.
Zagadnienie Dirichleta dla równania Poissona.
Metoda najszybszego spadku.
Liczba podprzedziałów: N = 10
Zadana liczba iteracji: iter = 300
Dokładność obliczeń: eps = 1.0E-0006
. . . . . . . . . . . . . . . . . . . .
Liczba wykonanych iteracji: 146
Wartości funkcji u(x[i],y[j]) dla i,j = 0,1,...,N:
i j x[i] y[j] u[i,j] błąd
0 0 0.00 0.00 0.000000000E+0000 0.0E+0000
0 1 0.00 0.10 0.000000000E+0000 0.0E+0000
0 2 0.00 0.20 0.000000000E+0000 0.0E+0000
0 3 0.00 0.30 0.000000000E+0000 0.0E+0000
0 4 0.00 0.40 0.000000000E+0000 0.0E+0000
0 5 0.00 0.50 0.000000000E+0000 0.0E+0000
0 6 0.00 0.60 0.000000000E+0000 0.0E+0000
0 7 0.00 0.70 0.000000000E+0000 0.0E+0000
0 8 0.00 0.80 0.000000000E+0000 0.0E+0000
0 9 0.00 0.90 0.000000000E+0000 0.0E+0000
0 10 0.00 1.00 0.000000000E+0000 0.0E+0000
1 0 0.10 0.00 0.000000000E+0000 0.0E+0000
1 1 0.10 0.10 8.099016914E-0003 9.8E-0007
1 2 0.10 0.20 1.439822150E-0002 1.8E-0006
1 3 0.10 0.30 1.889742625E-0002 2.6E-0006
1 4 0.10 0.40 2.159712234E-0002 2.9E-0006
1 5 0.10 0.50 2.249681867E-0002 3.2E-0006
1 6 0.10 0.60 2.159712234E-0002 2.9E-0006
1 7 0.10 0.70 1.889742625E-0002 2.6E-0006
1 8 0.10 0.80 1.439822150E-0002 1.8E-0006
1 9 0.10 0.90 8.099016914E-0003 9.8E-0007
1 10 0.10 1.00 0.000000000E+0000 0.0E+0000
2 0 0.20 0.00 0.000000000E+0000 0.0E+0000
2 1 0.20 0.10 1.439822150E-0002 1.8E-0006
2 2 0.20 0.20 2.559644316E-0002 3.6E-0006
2 3 0.20 0.30 3.359534385E-0002 4.7E-0006
2 4 0.20 0.40 3.839424491E-0002 5.8E-0006
2 5 0.20 0.50 3.999424468E-0002 5.8E-0006
2 6 0.20 0.60 3.839424492E-0002 5.8E-0006
2 7 0.20 0.70 3.359534385E-0002 4.7E-0006
2 8 0.20 0.80 2.559644316E-0002 3.6E-0006
2 9 0.20 0.90 1.439822150E-0002 1.8E-0006
2 10 0.20 1.00 0.000000000E+0000 0.0E+0000
3 0 0.30 0.00 0.000000000E+0000 0.0E+0000
3 1 0.30 0.10 1.889742625E-0002 2.6E-0006
3 2 0.30 0.20 3.359534385E-0002 4.7E-0006
3 3 0.30 0.30 4.409326183E-0002 6.7E-0006
3 4 0.30 0.40 5.039246619E-0002 7.5E-0006
3 5 0.30 0.50 5.249167116E-0002 8.3E-0006
3 6 0.30 0.60 5.039246619E-0002 7.5E-0006
3 7 0.30 0.70 4.409326183E-0002 6.7E-0006
3 8 0.30 0.80 3.359534385E-0002 4.7E-0006
3 9 0.30 0.90 1.889742625E-0002 2.6E-0006
3 10 0.30 1.00 0.000000000E+0000 0.0E+0000
4 0 0.40 0.00 0.000000000E+0000 0.0E+0000
4 1 0.40 0.10 2.159712234E-0002 2.9E-0006
4 2 0.40 0.20 3.839424491E-0002 5.8E-0006
4 3 0.40 0.30 5.039246619E-0002 7.5E-0006
4 4 0.40 0.40 5.759068808E-0002 9.3E-0006
4 5 0.40 0.50 5.999068770E-0002 9.3E-0006
4 6 0.40 0.60 5.759068808E-0002 9.3E-0006
4 7 0.40 0.70 5.039246619E-0002 7.5E-0006
4 8 0.40 0.80 3.839424492E-0002 5.8E-0006
4 9 0.40 0.90 2.159712234E-0002 2.9E-0006
4 10 0.40 1.00 0.000000000E+0000 0.0E+0000
5 0 0.50 0.00 0.000000000E+0000 0.0E+0000
5 1 0.50 0.10 2.249681867E-0002 3.2E-0006
5 2 0.50 0.20 3.999424468E-0002 5.8E-0006
5 3 0.50 0.30 5.249167116E-0002 8.3E-0006
5 4 0.50 0.40 5.999068770E-0002 9.3E-0006
5 5 0.50 0.50 6.248970499E-0002 1.0E-0005
. . . . . . . . . . . . . . . . . . . . . . . . . . .
PROGRAM 7.4.
Zagadnienie Dirichleta dla równania Poissona.
Metoda sprzężonych gradientów.
Liczba podprzedziałów: N = 10
Zadana liczba iteracji: iter = 300
Dokładność obliczeń: eps = 1.0E-0006
. . . . . . . . . . . . . . . . . . . .
Liczba wykonanych iteracji: 11
Wartości funkcji u(x[i],y[j]) dla i,j = 0,1,...,N:
i j x[i] y[j] u[i,j] błąd
0 0 0.00 0.00 0.000000000E+0000 0.0E+0000
0 1 0.00 0.10 0.000000000E+0000 0.0E+0000
0 2 0.00 0.20 0.000000000E+0000 0.0E+0000
0 3 0.00 0.30 0.000000000E+0000 0.0E+0000
0 4 0.00 0.40 0.000000000E+0000 0.0E+0000
0 5 0.00 0.50 0.000000000E+0000 0.0E+0000
0 6 0.00 0.60 0.000000000E+0000 0.0E+0000
0 7 0.00 0.70 0.000000000E+0000 0.0E+0000
0 8 0.00 0.80 0.000000000E+0000 0.0E+0000
0 9 0.00 0.90 0.000000000E+0000 0.0E+0000
0 10 0.00 1.00 0.000000000E+0000 0.0E+0000
1 0 0.10 0.00 0.000000000E+0000 0.0E+0000
1 1 0.10 0.10 8.099956395E-0003 4.4E-0008
1 2 0.10 0.20 1.439997319E-0002 2.7E-0008
1 3 0.10 0.30 1.890003408E-0002 -3.4E-0008
1 4 0.10 0.40 2.160002003E-0002 -2.0E-0008
1 5 0.10 0.50 2.249997382E-0002 2.6E-0008
1 6 0.10 0.60 2.160002003E-0002 -2.0E-0008
1 7 0.10 0.70 1.890003408E-0002 -3.4E-0008
1 8 0.10 0.80 1.439997319E-0002 2.7E-0008
1 9 0.10 0.90 8.099956395E-0003 4.4E-0008
1 10 0.10 1.00 0.000000000E+0000 0.0E+0000
2 0 0.20 0.00 0.000000000E+0000 0.0E+0000
2 1 0.20 0.10 1.439997319E-0002 2.7E-0008
2 2 0.20 0.20 2.559996879E-0002 3.1E-0008
2 3 0.20 0.30 3.360001579E-0002 -1.6E-0008
2 4 0.20 0.40 3.839996794E-0002 3.2E-0008
2 5 0.20 0.50 4.000008786E-0002 -8.8E-0008
2 6 0.20 0.60 3.839996794E-0002 3.2E-0008
2 7 0.20 0.70 3.360001579E-0002 -1.6E-0008
2 8 0.20 0.80 2.559996879E-0002 3.1E-0008
2 9 0.20 0.90 1.439997319E-0002 2.7E-0008
2 10 0.20 1.00 0.000000000E+0000 0.0E+0000
3 0 0.30 0.00 0.000000000E+0000 0.0E+0000
3 1 0.30 0.10 1.890003408E-0002 -3.4E-0008
3 2 0.30 0.20 3.360001579E-0002 -1.6E-0008
3 3 0.30 0.30 4.410007917E-0002 -7.9E-0008
3 4 0.30 0.40 5.039993835E-0002 6.2E-0008
3 5 0.30 0.50 5.249993484E-0002 6.5E-0008
3 6 0.30 0.60 5.039993835E-0002 6.2E-0008
3 7 0.30 0.70 4.410007917E-0002 -7.9E-0008
3 8 0.30 0.80 3.360001579E-0002 -1.6E-0008
3 9 0.30 0.90 1.890003408E-0002 -3.4E-0008
3 10 0.30 1.00 0.000000000E+0000 0.0E+0000
4 0 0.40 0.00 0.000000000E+0000 0.0E+0000
4 1 0.40 0.10 2.160002003E-0002 -2.0E-0008
4 2 0.40 0.20 3.839996794E-0002 3.2E-0008
4 3 0.40 0.30 5.039993835E-0002 6.2E-0008
4 4 0.40 0.40 5.760007085E-0002 -7.1E-0008
4 5 0.40 0.50 6.000001397E-0002 -1.4E-0008
4 6 0.40 0.60 5.760007085E-0002 -7.1E-0008
4 7 0.40 0.70 5.039993835E-0002 6.2E-0008
4 8 0.40 0.80 3.839996794E-0002 3.2E-0008
4 9 0.40 0.90 2.160002003E-0002 -2.0E-0008
4 10 0.40 1.00 0.000000000E+0000 0.0E+0000
5 0 0.50 0.00 0.000000000E+0000 0.0E+0000
5 1 0.50 0.10 2.249997382E-0002 2.6E-0008
5 2 0.50 0.20 4.000008786E-0002 -8.8E-0008
5 3 0.50 0.30 5.249993484E-0002 6.5E-0008
5 4 0.50 0.40 6.000001397E-0002 -1.4E-0008
5 5 0.50 0.50 6.249996603E-0002 3.4E-0008
. . . . . . . . . . . . . . . . . . . . . . . . . . .
Do rozwiązywania układu równań (7.100) metodą Stone'a został napisany oddzielny program 7.5. Tabulogram modułu Obliczenia tego programu oraz uzyskane za jego pomocą wyniki obliczeń dla zagadnienia (7.108) - (7.109) są następujące:
{program 7.5}
unit Obliczenia;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls,
Forms, Dialogs, StdCtrls, Buttons;
type
Tabl = array[0..100] of Real;
. . . . . . . . . . . . . . . . . . . . . . . . . .
var
Form3: TForm3;
fi,lw,ls,lp,un,ue,ron,rn,de: array[0..2500] of Real;
i,ii,iter,j,jj,k,l,licz,n,m,n1,n2,nr: Integer;
al,bl,dt,eps,h,h2,p,p1,p2,un1,x,y: Real;
ar,u,r: array[0..40,0..40] of Real;
aa,bb,cc,dd,up: Tabl;
plik: Text;
implementation
uses Ustawienia, Informacje, Grafika, Podglad;
{$R *.DFM}
{function f(x,y: Real): Real;}
{function ud(x,y: Real): Real;}
{procedure Tridiag1(n: Integer; a,b,c,d: Tabl;
var x: Tabl);}
{function akl(l,k,n1: Integer): Real;}
function ap(l: Integer): Real;
begin
if (l<1) then exit;
ap:=4
end;
function an(l,n1: Integer): Real;
begin
an:=-1;
if ((l-1) div n1=(l-1)/n1) then an:=0;
end;
function ass(l,n1: Integer): Real;
begin
ass:=-1;
if ((l div n1)=l/n1) then ass:=0;
end;
function ae(l,n1: Integer): Real;
begin
ae:=-1;
if (l<=n1) then ae:=0;
end;
function aw(l,n1: Integer): Real;
begin
aw:=-1;
if (l>n1*(n1-1)) then aw:=0;
end;
. . . . . . . . . . . . . . . . . . . . . .
procedure TForm3.BitBtn1Click(Sender: TObject);
label et1,et2;
begin
Form2.Show;
AssignFile(plik,Edit5.Text);
Rewrite(plik); Writeln(plik,'PROGRAM 7.5.');
Write(plik,'Zagadnienie Dirichleta');
Writeln(plik,' dla równania Poissona.');
Writeln(plik,'Metoda Stone`a. {Strongly Implicit Procedure)');
n:=StrToInt(Edit1.Text);
iter:=StrToInt(Edit2.Text);
eps:=StrToFloat(Edit3.Text);
al:=StrToFloat(Edit4.Text);
n1:=n-1; h:=1/n; m:=n1*n1;
for l:=1 to m do fi[l]:=0;
un[1]:=0;
for l:=1 to n1 do
ue[l]:=0;
lp[1]:=ap(1);
un[2]:=an(2,n1)/lp[1];
ue[n1+1]:=ae(n1+1,n1)/lp[1];
ls[1]:=ass(1,n1)/(1+al*ue[n1+1]);
lw[1]:=aw(1,n1)/(1+al*un[2]);
for l:=2 to n1 do begin
lp[l]:=ap(l)+al*ue[n1+l-1]*ls[l-1]-ls[l-1]*un[l];
un[l+1]:=an(l+1,n1)/lp[l];
ue[n1+l]:=(ae(n1+l,n1)-al*ue[n1+l-1]*ls[l-1])/lp[l];
ls[l]:=ass(l,n1)/(1+al*ue[n1+l]);
lw[l]:=aw(l,n1)/(1+al*un[l+1]);
end;
for l:=n1+1 to m-n1 do begin
lp[l]:=ap(l)+al*(lw[l-n1]*un[l-n1+1]+ue[l+n1-1]*ls[l-1])-
ls[l-1]*un[l]-lw[l-n1]*ue[l];
un[l+1]:=(an(l+1,n1)-al*lw[l-n1]*un[l+1-n1])/lp[l];
ue[n1+l]:=(ae(n1+l,n1)-al*ue[n1+l-1]*ls[l-1])/lp[l];
ls[l]:=ass(l,n1)/(1+al*ue[l+n1]);
lw[l]:=aw(l,n1)/(1+al*un[l+1]);
end;
for l:=m-n1+1 to m-1 do begin
lp[l]:=ap(l)+al*(lw[l-n1]*un[l-n1+1]+ue[l+n1-1]*ls[l-1])-
ls[l-1]*un[l]-lw[l-n1]*ue[l];
un[l+1]:=(an(l+1,n1)-al*lw[l-n1]*un[l+1-n1])/lp[l];
ls[l]:=ass(l,n1)/(1+al*ue[l+n1]);
end;
lp[m]:=ap(m)+al*(lw[m-n1]*un[m-n1+1]+ue[m+n1-1]*ls[m-1])-
ls[m-1]*un[m]-lw[m-n1]*ue[m];
Writeln(plik);
Writeln(plik,'Liczba podprzedziałów: N = ',n:4);
Writeln(plik,'Zadana liczba iteracji: iter = ',iter:4);
Writeln(plik,'Dokładność obliczeń: eps = ',eps:8);
Writeln(plik,'Parametr relaksacyjny: al = ',al:8);
licz:=0; Writeln(plik);
et2: licz:=licz+1;
for k:=1 to m do begin
p:=0;
for l:=1 to m do
p:=p+akl(k,l,n1)*fi[l];
ron[k]:=p;
end;
l:=0;
for i:=1 to n1 do begin
x:=i*h;
for j:=1 to n1 do begin
l:=l+1; y:=j*h;
ron[l]:=-h*h*f(x,y)-ron[l];
end;
end;
for l:=1 to m do begin
rn[l]:=ron[l]/lp[l];
if ((l-1)>0) then
rn[l]:=(ron[l]-ls[l-1]*rn[l-1])/lp[l];
if ((l-n1)>0) then
rn[l]:=(ron[l]-ls[l-1]*rn[l-1]-lw[l-n1]*rn[l-n1])/lp[l];
end;
bl:=0;
for l:=m downto 1 do begin
de[l]:=rn[l];
if ((l+1)<=m) then
de[l]:=rn[l]-un[l+1]*de[l+1];
if ((l+n1)<=m) then
de[l]:=rn[l]-un[l+1]*de[l+1]-ue[l+n1]*de[l+n1];
if (Abs(de[l])>bl) then bl:=Abs(de[l]);
end;
Writeln(plik,'iter = ',licz:3,' ','bl = ',bl:9);
for l:=1 to m do fi[l]:=fi[l]+de[l];
if (bl<eps) then goto et1;
if (licz<iter) then goto et2;
et1:
Writeln(plik);
Writeln(plik,'Liczba wykonanych iteracji: ',licz:3);
Writeln(plik);
Write(plik,'Wartości funkcji u(x[i],y[j])');
Writeln(plik,' dla i,j = 0,1,...,N:');
Write(plik,' i j x[i] y[j] fi[i,j]');
Writeln(plik,' błąd');
l:=0;
for i:=1 to n1 do begin
x:=i*h;
for j:=1 to n1 do begin
l:=l+1; y:=j*h; bl:=fi[l]-ud(x,y);
Writeln(plik,i:3,' ',j:3,' ',x:5:2,' ',y:5:2,' ',
fi[l]:18,' ',bl:9);
end;
end;
Writeln(plik); CloseFile(plik);
Form2.Wyniki.Lines.LoadFromFile(Edit5.Text);
end;
. . . . . . . . . . . . . . . . . . . . . .
procedure TForm3.BitBtn3Click(Sender: TObject);
begin
Close;
end;
end.
PROGRAM 7.5.
Zagadnienie Dirichleta dla równania Poissona.
Metoda Stone`a. {Strongly Implicit Procedure)
Liczba podprzedziałów: N = 10
Zadana liczba iteracji: iter = 100
Dokładność obliczeń: eps = 1.0E-0006
Parametr relaksacyjny: al = 5.0E-0001
. . . . . . . . . . . . . . . . . . . .
Liczba wykonanych iteracji: 31
Wartości funkcji u(x[i],y[j]) dla i,j = 0,1,...,N:
i j x[i] y[j] fi[i,j] błąd
1 1 0.10 0.10 9.628068544E-0002 7.9E-0004
1 2 0.10 0.20 1.831367373E-0001 1.5E-0003
1 3 0.10 0.30 2.520660766E-0001 2.1E-0003
1 4 0.10 0.40 2.963214247E-0001 2.4E-0003
1 5 0.10 0.50 3.115707641E-0001 2.6E-0003
1 6 0.10 0.60 2.963213863E-0001 2.4E-0003
1 7 0.10 0.70 2.520660096E-0001 2.1E-0003
1 8 0.10 0.80 1.831366615E-0001 1.5E-0003
1 9 0.10 0.90 9.628063145E-0002 7.9E-0004
2 1 0.20 0.10 1.831367373E-0001 1.5E-0003
2 2 0.20 0.20 3.483467581E-0001 2.9E-0003
2 3 0.20 0.30 4.794581503E-0001 3.9E-0003
2 4 0.20 0.40 5.636368267E-0001 4.6E-0003
2 5 0.20 0.50 5.926427992E-0001 4.9E-0003
2 6 0.20 0.60 5.636367664E-0001 4.6E-0003
2 7 0.20 0.70 4.794580452E-0001 3.9E-0003
2 8 0.20 0.80 3.483466403E-0001 2.9E-0003
2 9 0.20 0.90 1.831366564E-0001 1.5E-0003
3 1 0.30 0.10 2.520660766E-0001 2.1E-0003
3 2 0.30 0.20 4.794581503E-0001 3.9E-0003
3 3 0.30 0.30 6.599174970E-0001 5.4E-0003
3 4 0.30 0.40 7.757795098E-0001 6.4E-0003
3 5 0.30 0.50 8.157028160E-0001 6.7E-0003
3 6 0.30 0.60 7.757794498E-0001 6.4E-0003
3 7 0.30 0.70 6.599173926E-0001 5.4E-0003
3 8 0.30 0.80 4.794580341E-0001 3.9E-0003
3 9 0.30 0.90 2.520659984E-0001 2.1E-0003
4 1 0.40 0.10 2.963214247E-0001 2.4E-0003
4 2 0.40 0.20 5.636368267E-0001 4.6E-0003
4 3 0.40 0.30 7.757795098E-0001 6.4E-0003
4 4 0.40 0.40 9.119834816E-0001 7.5E-0003
4 5 0.40 0.50 9.589161557E-0001 7.9E-0003
4 6 0.40 0.60 9.119834393E-0001 7.5E-0003
4 7 0.40 0.70 7.757794360E-0001 6.4E-0003
4 8 0.40 0.80 5.636367443E-0001 4.6E-0003
4 9 0.40 0.90 2.963213700E-0001 2.4E-0003
5 1 0.50 0.10 3.115707641E-0001 2.6E-0003
5 2 0.50 0.20 5.926427992E-0001 4.9E-0003
5 3 0.50 0.30 8.157028160E-0001 6.7E-0003
5 4 0.50 0.40 9.589161557E-0001 7.9E-0003
5 5 0.50 0.50 1.008264104E+0000 8.3E-0003
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
PROGRAM 7.5.
Zagadnienie Dirichleta dla równania Poissona.
Metoda Stone`a. {Strongly Implicit Procedure)
Liczba podprzedziałów: N = 20
Zadana liczba iteracji: iter = 200
Dokładność obliczeń: eps = 1.0E-0006
Parametr relaksacyjny: al = 5.0E-0001
. . . . . . . . . . . . . . . . . . . .
Liczba wykonanych iteracji: 99
Wartości funkcji u(x[i],y[j]) dla i,j = 0,1,...,N:
i j x[i] y[j] fi[i,j] błąd
1 1 0.05 0.05 2.452195651E-0002 5.0E-0005
1 2 0.05 0.10 4.844009700E-0002 9.9E-0005
1 3 0.05 0.15 7.116547580E-0002 1.5E-0004
1 4 0.05 0.20 9.213852064E-0002 1.9E-0004
1 5 0.05 0.25 1.108428068E-0001 2.3E-0004
1 6 0.05 0.30 1.268177736E-0001 2.6E-0004
1 7 0.05 0.35 1.396700646E-0001 2.9E-0004
1 8 0.05 0.40 1.490832143E-0001 3.1E-0004
1 9 0.05 0.45 1.548254401E-0001 3.2E-0004
1 10 0.05 0.50 1.567553494E-0001 3.2E-0004
1 11 0.05 0.55 1.548254219E-0001 3.2E-0004
1 12 0.05 0.60 1.490831789E-0001 3.1E-0004
1 13 0.05 0.65 1.396700139E-0001 2.9E-0004
1 14 0.05 0.70 1.268177104E-0001 2.6E-0004
1 15 0.05 0.75 1.108427352E-0001 2.3E-0004
1 16 0.05 0.80 9.213844578E-0002 1.9E-0004
1 17 0.05 0.85 7.116540427E-0002 1.5E-0004
1 18 0.05 0.90 4.844003752E-0002 9.9E-0005
1 19 0.05 0.95 2.452192091E-0002 5.0E-0005
2 1 0.10 0.05 4.844009700E-0002 9.9E-0005
2 2 0.10 0.10 9.568743048E-0002 2.0E-0004
2 3 0.10 0.15 1.405786118E-0001 2.9E-0004
2 4 0.10 0.20 1.820082745E-0001 3.7E-0004
2 5 0.10 0.25 2.189562849E-0001 4.5E-0004
2 6 0.10 0.30 2.505128618E-0001 5.1E-0004
2 7 0.10 0.35 2.759009785E-0001 5.6E-0004
2 8 0.10 0.40 2.944954959E-0001 6.0E-0004
2 9 0.10 0.45 3.058385559E-0001 6.3E-0004
2 10 0.10 0.50 3.096508554E-0001 6.3E-0004
2 11 0.10 0.55 3.058385232E-0001 6.3E-0004
2 12 0.10 0.60 2.944954322E-0001 6.0E-0004
2 13 0.10 0.65 2.759008873E-0001 5.6E-0004
2 14 0.10 0.70 2.505127485E-0001 5.1E-0004
2 15 0.10 0.75 2.189561568E-0001 4.5E-0004
2 16 0.10 0.80 1.820081410E-0001 3.7E-0004
2 17 0.10 0.85 1.405784849E-0001 2.9E-0004
2 18 0.10 0.90 9.568732586E-0002 2.0E-0004
2 19 0.10 0.95 4.844003562E-0002 9.9E-0005
3 1 0.15 0.05 7.116547580E-0002 1.5E-0004
3 2 0.15 0.10 1.405786118E-0001 2.9E-0004
3 3 0.15 0.15 2.065302233E-0001 4.2E-0004
3 4 0.15 0.20 2.673963665E-0001 5.5E-0004
3 5 0.15 0.25 3.216783180E-0001 6.6E-0004
3 6 0.15 0.30 3.680394776E-0001 7.5E-0004
3 7 0.15 0.35 4.053382810E-0001 8.3E-0004
3 8 0.15 0.40 4.326563087E-0001 8.9E-0004
3 9 0.15 0.45 4.493209010E-0001 9.2E-0004
3 10 0.15 0.50 4.549217211E-0001 9.3E-0004
3 11 0.15 0.55 4.493208589E-0001 9.2E-0004
3 12 0.15 0.60 4.326562267E-0001 8.9E-0004
3 13 0.15 0.65 4.053381639E-0001 8.3E-0004
3 14 0.15 0.70 3.680393324E-0001 7.5E-0004
3 15 0.15 0.75 3.216781543E-0001 6.6E-0004
3 16 0.15 0.80 2.673961967E-0001 5.5E-0004
3 17 0.15 0.85 2.065300628E-0001 4.2E-0004
3 18 0.15 0.90 1.405784808E-0001 2.9E-0004
3 19 0.15 0.95 7.116539993E-0002 1.5E-0004
4 1 0.20 0.05 9.213852064E-0002 1.9E-0004
4 2 0.20 0.10 1.820082745E-0001 3.7E-0004
4 3 0.20 0.15 2.673963665E-0001 5.5E-0004
4 4 0.20 0.20 3.462002630E-0001 7.1E-0004
4 5 0.20 0.25 4.164795535E-0001 8.5E-0004
4 6 0.20 0.30 4.765037308E-0001 9.8E-0004
4 7 0.20 0.35 5.247948015E-0001 1.0E-0003
4 8 0.20 0.40 5.601636804E-0001 1.1E-0003
4 9 0.20 0.45 5.817394691E-0001 1.1E-0003
4 10 0.20 0.50 5.889909010E-0001 1.2E-0003
4 11 0.20 0.55 5.817394225E-0001 1.1E-0003
4 12 0.20 0.60 5.601635897E-0001 1.1E-0003
4 13 0.20 0.65 5.247946722E-0001 1.0E-0003
4 14 0.20 0.70 4.765035707E-0001 9.8E-0004
4 15 0.20 0.75 4.164793736E-0001 8.5E-0004
4 16 0.20 0.80 3.462000768E-0001 7.1E-0004
4 17 0.20 0.85 2.673961914E-0001 5.5E-0004
4 18 0.20 0.90 1.820081322E-0001 3.7E-0004
4 19 0.20 0.95 9.213843888E-0002 1.9E-0004
5 1 0.25 0.05 1.108428068E-0001 2.3E-0004
5 2 0.25 0.10 2.189562849E-0001 4.5E-0004
5 3 0.25 0.15 3.216783180E-0001 6.6E-0004
5 4 0.25 0.20 4.164795535E-0001 8.5E-0004
5 5 0.25 0.25 5.010256738E-0001 1.0E-0003
5 6 0.25 0.30 5.732348747E-0001 1.1E-0003
5 7 0.25 0.35 6.313291273E-0001 1.2E-0003
5 8 0.25 0.40 6.738779594E-0001 1.3E-0003
5 9 0.25 0.45 6.998336785E-0001 1.4E-0003
5 10 0.25 0.50 7.085571694E-0001 1.4E-0003
5 11 0.25 0.55 6.998336317E-0001 1.4E-0003
5 12 0.25 0.60 6.738778685E-0001 1.3E-0003
5 13 0.25 0.65 6.313289978E-0001 1.2E-0003
5 14 0.25 0.70 5.732347146E-0001 1.1E-0003
5 15 0.25 0.75 5.010254941E-0001 1.0E-0003
5 16 0.25 0.80 4.164793680E-0001 8.5E-0004
5 17 0.25 0.85 3.216781437E-0001 6.6E-0004
5 18 0.25 0.90 2.189561436E-0001 4.5E-0004
5 19 0.25 0.95 1.108427259E-0001 2.3E-0004
6 1 0.30 0.05 1.268177736E-0001 2.6E-0004
6 2 0.30 0.10 2.505128618E-0001 5.1E-0004
6 3 0.30 0.15 3.680394776E-0001 7.5E-0004
6 4 0.30 0.20 4.765037308E-0001 9.8E-0004
6 5 0.30 0.25 5.732348747E-0001 1.1E-0003
6 6 0.30 0.30 6.558510694E-0001 1.3E-0003
6 7 0.30 0.35 7.223180314E-0001 1.4E-0003
6 8 0.30 0.40 7.709991242E-0001 1.5E-0003
6 9 0.30 0.45 8.006956589E-0001 1.6E-0003
6 10 0.30 0.50 8.106764089E-0001 1.7E-0003
6 11 0.30 0.55 8.006956157E-0001 1.6E-0003
6 12 0.30 0.60 7.709990404E-0001 1.5E-0003
6 13 0.30 0.65 7.223179118E-0001 1.4E-0003
6 14 0.30 0.70 6.558509218E-0001 1.3E-0003
6 15 0.30 0.75 5.732347089E-0001 1.1E-0003
6 16 0.30 0.80 4.765035596E-0001 9.8E-0004
6 17 0.30 0.85 3.680393168E-0001 7.5E-0004
6 18 0.30 0.90 2.505127313E-0001 5.1E-0004
6 19 0.30 0.95 1.268176988E-0001 2.6E-0004
7 1 0.35 0.05 1.396700646E-0001 2.9E-0004
7 2 0.35 0.10 2.759009785E-0001 5.6E-0004
7 3 0.35 0.15 4.053382810E-0001 8.3E-0004
7 4 0.35 0.20 5.247948015E-0001 1.0E-0003
7 5 0.35 0.25 6.313291273E-0001 1.2E-0003
7 6 0.35 0.30 7.223180314E-0001 1.4E-0003
7 7 0.35 0.35 7.955210660E-0001 1.6E-0003
7 8 0.35 0.40 8.491357304E-0001 1.7E-0003
7 9 0.35 0.45 8.818418543E-0001 1.8E-0003
7 10 0.35 0.50 8.928341051E-0001 1.8E-0003
7 11 0.35 0.55 8.818418177E-0001 1.8E-0003
7 12 0.35 0.60 8.491356593E-0001 1.7E-0003
7 13 0.35 0.65 7.955209647E-0001 1.6E-0003
7 14 0.35 0.70 7.223179061E-0001 1.4E-0003
7 15 0.35 0.75 6.313289866E-0001 1.2E-0003
7 16 0.35 0.80 5.247946559E-0001 1.0E-0003
7 17 0.35 0.85 4.053381436E-0001 8.3E-0004
7 18 0.35 0.90 2.759008664E-0001 5.6E-0004
7 19 0.35 0.95 1.396700003E-0001 2.9E-0004
8 1 0.40 0.05 1.490832143E-0001 3.1E-0004
8 2 0.40 0.10 2.944954959E-0001 6.0E-0004
8 3 0.40 0.15 4.326563087E-0001 8.9E-0004
8 4 0.40 0.20 5.601636804E-0001 1.1E-0003
8 5 0.40 0.25 6.738779594E-0001 1.3E-0003
8 6 0.40 0.30 7.709991242E-0001 1.5E-0003
8 7 0.40 0.35 8.491357304E-0001 1.7E-0003
8 8 0.40 0.40 9.063637959E-0001 1.9E-0003
8 9 0.40 0.45 9.412741765E-0001 1.9E-0003
8 10 0.40 0.50 9.530072632E-0001 2.0E-0003
8 11 0.40 0.55 9.412741488E-0001 1.9E-0003
8 12 0.40 0.60 9.063637422E-0001 1.9E-0003
8 13 0.40 0.65 8.491356537E-0001 1.7E-0003
8 14 0.40 0.70 7.709990292E-0001 1.5E-0003
8 15 0.40 0.75 6.738778521E-0001 1.3E-0003
8 16 0.40 0.80 5.601635687E-0001 1.1E-0003
8 17 0.40 0.85 4.326562024E-0001 8.9E-0004
8 18 0.40 0.90 2.944954082E-0001 6.0E-0004
8 19 0.40 0.95 1.490831638E-0001 3.1E-0004
516 7. Równania różniczkowe cząstkowe
7.6. Siatkowe równania eliptyczne 515
Wyszukiwarka