Laboratorium Wytrzymałości Materiałów |
||
Magdalena Nowak Natalia Mrozikiewicz Krzysztof Nowakowski Tomasz Olejniczak |
Ćwiczenie nr 1 Pomiar naprężeń w zginanym dwuteowniku |
|
Data Ćw: 19.05.2006 |
Data Oddania: 02.06.2006 |
|
Szkic belki z usytuowaniem tensometrów:
Oznaczenie dwuteownika:
I100
Iz = 1710000mm4
Smax = 19900mm3
Opis stanowiska pomiarowego.
Do przeprowadzonego ćwiczenia zastosowany został układ tensometryczny
mostka Wheatstone`a z aparaturą wzmacniającą. Wykorzystany został również
układ o zwiększonej czułości: rozetę tensometryczną dwuczujnikową.
Tablica z wynikami pomiarowymi:
Lp. |
x |
Zmierzone |
Teoretyczne |
||||
|
|
uD |
σA |
τC |
uD |
σA |
τC |
|
mm |
mm |
MPa |
MPa |
mm |
MPa |
MPa |
1 |
250 |
0,369 |
53,0 |
18,4 |
- |
54,8 |
16,5 |
2 |
200 |
0,374 |
42,5 |
17,2 |
- |
43,9 |
16,5 |
3 |
150 |
0,367 |
31,6 |
17,1 |
- |
32,8 |
16,5 |
4 |
100 |
0,366 |
21,3 |
17,6 |
- |
21,9 |
16,5 |
Średnia |
0,369 |
- |
17,6 |
0,379 |
- |
- |
|
Obliczenie ugięcia w środku belki:
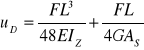
uD = 0,379
Teoretyczne obliczenia naprężeń w belce:
Obliczenie teoretycznych σ
RA= RB = P/2 = 7,5 kN
Siła poprzeczna T jest przedziałami stała, jej wartość T = RA= RB = 7,5kN
Moment gnący:
MX = RB· x , dla x = 0 ⇒ MX = 0
x = l/2 = 0,35m ⇒ MX = RB * l/2 = 7,5kN* 0,35m = 2,625kNm
Mmzx = 2,62kNm
Obliczenie momentów gnących z proporcji:
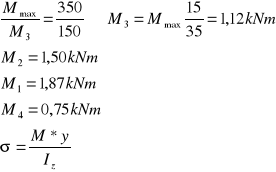
σ obliczmy we włóknach skrajnych y = 1/2 h = 50mm

Wyliczenie teoretycznego τ:
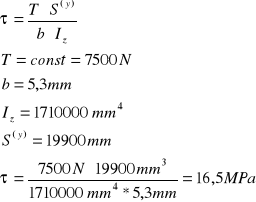
Wnioski:
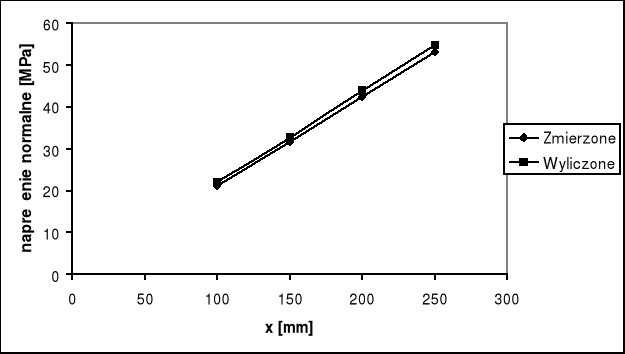
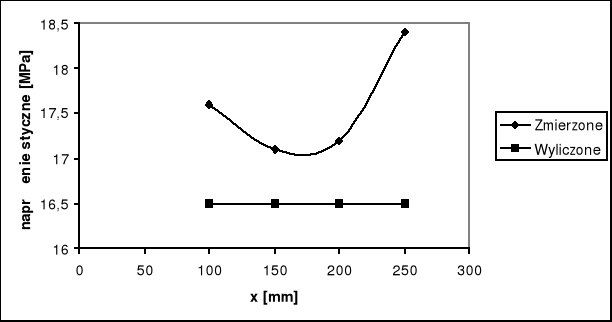
Wyniki otrzymane podczas ćwiczenia są zbliżone do wartości teoretycznych. Wyniki otrzymane doświadczalnie rosną w miarę zbliżania się do punktu przyłożenia siły, w przypadku obliczeń teoretycznych, naprężenia styczne zależą od siły poprzecznej, są więc teoretycznie stałe.Wykresy:
Wyszukiwarka