Wyznaczyć metodą relaksacji 3 kolejne przybliżenia rozwiązania równania:
![]()
, dla x>0
2. Kostka w kształcie sześcianu o boku równym 50 cm wraz ze wzrostem temperatury zwiększa swoją objętość z prędkością 2 cm3/h. Z jaką prędkością wydłużają się boki sześcianu? Jaka będzie długość boku po 90 minutach rozszerzania się kostki?
3. Obliczyć pochodną kierunkową funkcji 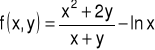
w punkcie P(-1,2)
w kierunku wektora ![]()
4. W roku 1970 światowa produkcja energii pierwotnej z węgla wynosiła W=62,96E+15 Btu. Roczna produkcja w latach 1970-2004 daje się opisać równaniem postaci:
![]()
a. Oszacować produkcję w roku 2007.
b. W którym roku produkcja zwiększy się dwukrotnie w stosunku do 1970?
c. Jaki jest górny pułap produkcji?
5. Koncentracja zanieczyszczenia w wodzie podziemnej w odległości x po czasie t wyraża się wzorem:
![]()
Oszacować C(x1,t1) dla wartości liczbowych:
x1=20 m, t1=20 dni, V=1,157 10-4 m/s, KL=1,16 10-4 m2/s
1. Obliczyć pochodną kierunkową funkcji 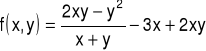
w punkcie P(2,-1) w kierunku wektora ![]()
2. Wyznaczyć metodą relaksacji 3 kolejne przybliżenia rozwiązania równania:
![]()
3. Łódź żegluje w stronę pionowego klifu ze stałą prędkością 5 km/h. Jak będzie się zmieniać odległość między łodzią a szczytem klifu, jeżeli w chwili pomiaru odległość łodzi od podnóża klifu wynosiła 2 km? Jaka będzie odległość łodzi od szczytu klifu po 15 minutach rejsu?
4. W roku 1970 światowa produkcja energii pierwotne z gazu ziemnego wynosiła
W=37.09E+15 Btu. Roczna produkcja w latach 1970-2004 daje się opisać równaniem postaci:
![]()
W roku 2004 produkcja wyniosła 102.19E=15 Btu.
a. Oszacować produkcję w roku 2007.
b. Jaki jest górny pułap produkcji?
5.Koncentracja zanieczyszczenia w wodzie podziemnej w odległości x po czasie t wyraża się wzorem:
![]()
Oszacować C(x1,t1) dla wartości liczbowych:
x1=199 m, t1=20 dni, V=1,157 10-4 m/s, KL=1,16 10-4 m2/s
Zad. 2. Rozwiązać równanie: 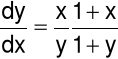
Zad.2. Rozwiąż równanie różniczkowe
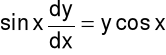
Zad.2. Rozwiąż równanie różniczkowe
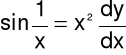
Zad. 4. Znaleźć pochodną 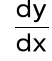
jeżeli ![]()
I. Kamień rzucony pionowo do góry z pewną prędkością początkową vo wznosi się w ciągu czasu t na wysokość h, daną równaniem: h = -5 t2 + 50 t. Znaleźć:
prędkość w chwili t = 0,
czas wznoszenia się kamienia
największe wzniesienie.
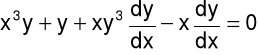
Zad. 3. Znaleźć przybliżone rozwiązanie równania metodą stycznych
![]()
Zad. 3. Znaleźć przybliżone rozwiązanie równania metodą cięciw
![]()
Zad. 6. Znaleźć metodą Newtona rozwiązanie przybliżone równania:
![]()
Zad. 6. Znaleźć metodą Newtona rozwiązanie przybliżone równania
![]()
Zad. 5 A. W wyniku pożaru na wiertni wytworzyło się pole temperaturowe. Rozkład temperatury opisuje funkcja:
![]()
Określić kierunek ucieczki ze strefy pożaru.
Zad. 5 B. W wyniku pożaru na wiertni wytworzyło się pole temperaturowe. Rozkład temperatury opisuje funkcja:
![]()
Określić kierunek ucieczki ze strefy pożaru.
Zad. 5 C. W wyniku pożaru na wiertni wytworzyło się pole temperaturowe. Rozkład temperatury opisuje funkcja:
![]()
Określić kierunek ucieczki ze strefy pożaru.
Zad. 5 D. W wyniku z otworu wiertniczego zaczął się wydobywać siarkowodór. Koncentrację stężenia kwasu opisuje funkcja:
![]()
Określić kierunek ucieczki ze strefy zagrożenia.
Zad. 5 E. W wyniku z otworu wiertniczego zaczął się wydobywać siarkowodór. Koncentrację stężenia kwasu opisuje funkcja:
![]()
![]()
iteracje, dla x>0
![]()
Newton
![]()
Newton, dla x>0
Zad. 6 C. Wyznaczyć metodą Newtona 3 kolejne przybliżenia rozwiązania równania: ![]()
Zad. 6 D. Wyznaczyć metodą Newtona 3 kolejne przybliżenia rozwiązania równania: ![]()
Zad. 6 E. Wyznaczyć metodą relaksacji 3 kolejne przybliżenia rozwiązania równania: ![]()
Zad. 6 F. Wyznaczyć metodą relaksacji 3 kolejne przybliżenia rozwiązania równania: 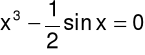
Zad. 6 G. Wyznaczyć metodą relaksacji 3 kolejne przybliżenia rozwiązania równania: ![]()
Łódź żegluje w stronę pionowego klifu ze stałą prędkością 5 km/h. Jak będzie się zmieniać odległość między łodzią a szczytem klifu, jeżeli w chwili pomiaru odległość łodzi od podnóża klifu wynosiła 2 km? Jaka będzie odległość łodzi od szczytu klifu po 15 minutach rejsu?
Kostka w kształcie sześcianu o boku równym 50 cm wraz ze wzrostem temperatury zwiększa swoją objętość z prędkością 2 cm3/h. Z jaką prędkością wydłużają się boki sześcianu? Jaka będzie długość boku po 1,5 godzinie rozszerzania się kostki?
Zbiornik płuczkowy na wiertni ma kształt prostopadłościanu o podstawie kwadratu o boku równym 10 m i wysokości 4 m. Jak szybko będzie opadać poziom płuczki, jeżeli zbiornik jest opróżniany ze stałą prędkością 2 m3/min? Jaka będzie głębokość cieczy w zbiorniku po czasie 1 godz?
Zagadnienia teoretyczne
Fcje wielu zmiennych skalarne i wektorowe, pochodne cząstkowe, różniczka zupełna
Def. i właściwości pochodnej kierunkowej i gradientu fcji, prawo Darcy'ego, modelowanie granic nieprzepuszczalnych
Fcje specjalne erf, erfc, Ei, definicje, właściwości asymptotyczne, wzory przybliżone
Metody przybliżone rozwiązywania równań algebraicznych, kryteria zbieżności
Pojęcie wektora normalnego do powierzchni
Iloczyn skalarny wektorów
Strumień wektora przez powierzchnię, obliczanie wydajności otworów
Teoria pola, laplasjan, divergencja
Tw. Gaussa-Ostrogragzkiego
Wsp. cylindryczne
Równ. Laplace'a, równ. ciągłości, równ. filtracji, równ. filtracji cieczy nieściśliwej
Wyszukiwarka