![]()
Akademia Techniczno-Humanistyczna w Bielsku-Białej
Wydział ...........................................
Kierunek ..........................................
Rok akademicki ..............................
Semestr ...........................................
Ćwiczenia laboratoryjne z Mechaniki Płynów
Ćwiczenie nr ......
Temat. . . . . . . . . . . . . . . . . . . . . . . . . .
Wykonali:
..……………………….
..……………………….
..……………………….
.………………………..
..……………………….
Data wykonania ćwiczenia……........................
Data przyjęcia sprawozdania………...................
1. Wstęp teoretyczny:
Stateczność płynu jest ściśle związana z liczbą Reynoldsa. Liczba Reynoldsa wynosi:
![]()
gdzie: c - prędkość przepływu
d - wymiar liniowy charakterystyczny dla obszaru przepływu
ν - lepkość kinematyczna płynu
Liczba Reynolds'a wyraża stosunek wielkości sił bezwładności do sił lepkości. Podczas przepływu cieczy lepkiej w rurze o przekroju kołowym i skończonej długości wymuszonego przez stałą w czasie różnicy ciśnień Δp obserwuje się ruchy :
laminarny, dla Re < Rekr1 , co wiąże się z niestatecznością ruchu nieustalonego. Nieustaloność może być spowodowana zaburzeniami na wejściu rury i niezależnie od ich intensywności tak powstały obszar ruchu nieustalonego będzie znoszony w dół przepływu, aż zostanie z rury usunięty
turbulentny, Re > Rekr1 ; aby powstał na całej długości rury wystarczą do tego tym mniejsze amplitudy im większa jest różnica Re - Rekr1. W tym sensie przepływ laminarny jest metastabilny, czyli niestateczny w stosunku do zaburzeń o skończonej amplitudzie.
Należy wspomnieć, że lepkość płynu ma działanie stabilizujące przepływ.
Liczby podobieństwa, zwane też liczbami kryterialnymi - to bezwymiarowe współczynniki stosowane w równaniach zachowania, opisujące układy fizyczne i sprowadzone do postaci bezwymiarowej, definiowane zwykle jako stosunek łatwo mierzalnych wielkości wymiarowych lub jako stosunek wyrazów opisujących dany proces w równaniach (np. liczba Reynoldsa jest stosunkiem członu adwekcyjnego do członu dyfuzyjnego w równaniu Naviera-Stokesa). Służą one zwykle do upraszczania rachunków fizycznych i inżynieryjnych, a ich wartość pozwala często na łatwe charakteryzowanie natury opisywanych przez nie zjawisk (jeżeli dwa układy posiadają taką samą wartość liczby bezwymiarowej, opisującej konkretny układ to znaczy, że układy te są dynamicznie podobne).
Najczęściej stosowanie liczby podobieństwa
liczba Eulera - Liczbę e można określić jako granicę pewnego ciągu liczbowego. Otóż można udowodnić, że ciąg o wyrazie ogólnym
|
jest rosnący i ograniczony z góry, a więc ma granicę. Z twierdzenia dowiadujemy się, że każdy ciąg liczbowy rosnący i ograniczony z góry ma granicę.
Ją właśnie oznaczamy przez e. Liczba e jest niewymierna i ma wartość przybliżoną ok. 2.718281828459. Jest też liczbą przestępną, tzn. nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych.
Przybliżoną wartość liczby e można obliczyć z dowolną dokładnością według wzoru
|
liczba Froude'a - jedna z liczb podobieństwa, opisująca wpływ siły ciężkości na zjawiska przepływu płynów. Jej nazwa pochodzi od Williama Froude'a.
Intuicyjnie, liczba Frouda określa stosunek energii kinetycznej cieczy do energii potencjalnej potrzebnej do odchylenia (wymuszenia) przepływu płynów (cieczy lub gazu).
v - prędkość przepływu płynu;
g - przyspieszenie ziemskie;
L - wymiar liniowy.
liczba Macha - liczba podobieństwa wyrażająca:
stosunek prędkości przepływu płynu w danym miejscu do prędkości dźwięku w tym płynie w tym samym miejscu.
stosunek prędkości obiektu poruszającego się w płynie do prędkości dźwięku w tym płynie niezakłóconym ruchem obiektu, czyli formalnie - w nieskończoności.
gdzie:
v - prędkość przepływu lub obiektu
a - prędkość dźwięku w płynie w danym miejscu lub - odpowiednio - w nieskończoności.
Nazwa pochodzi od austriackiego fizyka Ernsta Macha.
W powietrzu o temperaturze 15 °C prędkość dźwięku wynosi 340,3 m/s[1] (1225 km/h).
2. Cel ćwiczenia:
Celem ćwiczenia jest wyznaczenie krytycznej liczby Reynoldsa Rekr , odpowiadającej zmianie metastabilnego przepływu laminarnego w turbulentny.
3. Przebieg ćwiczenia
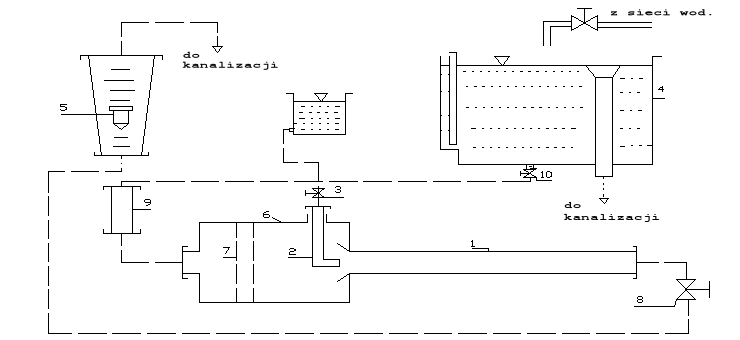
Stanowisko składa się z: rury pomiarowej (1) o średnicy d = 21mm, w której płynie woda, zacisku regulującego przepływ wody (8), dyszy doprowadzającej barwnik (2) , regulator szybkości wpływu barwnika (3), wąż gumowy, rotametr (5), rurowy zbiornik wyrównawczy (6), zaworu głównego (10), zespołu siatek z prostownicą (7), termometru (9), zbiornik
główny (4).
Odkręcamy zwór z barwnikiem, następnie zawór z wodą. Powoli zwiększamy prędkość przepływu cieczy. Początkowo barwnik płynący z wodą występuje jako jednolita smuga. Czekamy, aż smuga zmieni się w turbulencje. Wtedy odczytujemy temperaturę cieczy oraz prędkość cieczy. Wykonujemy dziesięć pomiarów i umieszczamy je w tabeli z wynikami. Kolejny krok to obliczenia.
![]()
Tabela z pomiarami
Numer pomiaru |
hkr [działki] |
Qkr [dm3/min] |
T [ºC] |
T[K] |
1. |
88 |
9,208 |
19,5 |
292,65 |
2. |
43 |
4,888 |
19 |
292,15 |
3. |
40 |
4,6 |
17 |
290,15 |
4. |
33 |
3,928 |
16,25 |
289,4 |
5. |
36,5 |
4,264 |
14,5 |
287,65 |
6. |
37 |
4,312 |
13,5 |
286,65 |
7. |
36,5 |
4,264 |
13 |
286,15 |
8. |
39 |
4,504 |
12,5 |
285,65 |
9. |
46 |
5,176 |
11,5 |
284,65 |
10. |
48 |
5,368 |
11 |
284,15 |
L.p. |
Qkr [m3/s] |
ckr [m/s] |
v [m2/s] |
Rekr |
1. |
1,53467*10-4 |
0,4435 |
1,05178*10-6 |
8853,137 |
2. |
8,14667*10-5 |
0,235 |
1,07171*10-6 |
4604,790 |
3. |
7,66667*10-5 |
0,2216 |
1,09134*10-6 |
4262,348 |
4. |
6,54667*10-5 |
0,1892 |
1,10122*10-6 |
3607,998 |
5. |
7,10667*10-5 |
0,2054 |
1,15095*10-6 |
3744,849 |
6. |
7,18667*10-5 |
0,2077 |
1,18081*10-6 |
3693,820 |
7. |
7,10667*10-5 |
0,2054 |
1,20075*10-6 |
3592,404 |
8. |
7,50667*10-5 |
0,2170 |
1,23069*10-6 |
3702,033 |
9. |
8,62667*10-5 |
0,2493 |
1,25056*10-6 |
4186,565 |
10. |
8,94667*10-5 |
0,2586 |
1,29051*10-6 |
4208,136 |
Przykładowe obliczenia
Qkr =9,208 ·(0,001/60) = 1,53*10-4[m3/s]
![]()
![]()
![]()
Re = ![]()
Wnioski:
Wraz ze spadkiem temperatury wody krytyczna liczba Reynoldsa wzrasta. Ponieważ, im niższa temperatura wody to tym wyższa gęstość wody.
W czasie doświadczenia można było zauważyć że przejście z ruchu laminarnego do turbulentnego następowało na skutek wszelakich drobnych zakłóceń np. lekkie uderzenie w zbiornik wyrównawczy. Na wielkość krytycznej liczby Reynoldsa mają wpływ również takie elementy jak: gładkość ścianek rury pomiarowej, czy np. ich drganie.