PRZETWARZANIE ROZPROSZONE:

Ma miejsce w sieciach stacji roboczych (sieciach lub systemów rozproszonych)

PRZETWARZANIE RÓWNOLEGŁE:

(w systemie klient- serwer) serwer www, serwer FTP. serwery pocztowe, serwer IRC, serwery baz danych

PRZETWARZANIE WSPÓŁBIEŻNE:

• dotyczy wielu niezależnych zadań

• umożliwia obsługę wielu zadań i minimalizację śred. czasu reakcji systemu na żądanie obsługi zadania użytkownika.

Furiera równanie: (przewodzenie ciepła)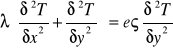

λ-współczynnik przewodnictwa ς- gęstość e- ciepło

Metoda stosowana do skomplikowanych geometrii. Dzieli się obiekt na elementy skończone, potem dyskretyzacja względem przestrzeni i w czasie (całkowanie względem czasu i po czasie)

eςMTⁿ⁺¹ ≠λΔtkTⁿ⁺¹=eςMTⁿ⁺¹+ bⁿ⁺¹

układ rozwiązujemy dla kolejnych kroków czasowych

temperatura w kroku następnym :A- macierz dana ATⁿ⁺¹=bⁿ

b- uwzględnia warunki brzegowe

szerokość półpasma W=2b-1

ZASADA POTOKOWOŚCI

Przetwarzanie potokowe - jak wykonać poszczególne instrukcje w komputerze:

1. wczytanie rozkazu

2. dekodowanie rozkazu

3. wczytanie danych

4. wykonanie operacji

5. zapisanie wyników do pamięci

6. wyznaczyć adres następnego rozkazu

Do każdego etapu mamy osobne urządzenia:

1) c=a-b

2) if c >0 then d = √c

else d=a+b

Architektura równoległa - klastracja

1. Flynn'a - liczba punktów instrukcji - liczba potoków danych

2. SISD single

3. MISD multiple

4. SIMD insert

5. MIMD data

Multiprocesor: programowanie jest bardziej zbliżone do oprogramowania komputerów sekwencyjnych, bo dane są zmiennymi globalnymi, wspólne dla procesorów, dostęp do pamięci jest wąski, (do 16), dlatego jest gorsza skalowalność

Multikomputer: zmienne są lokalne, duża dobra skalowalność, liczbę procesorów można zwiększyć tak jak wydajność. Komunikację trzeba programować

SMP - symetryczny multiprocesor, żaden procesor nie jest wyróżniony, ma dostęp do jądra

VSM virtual SM, DSM distributed SM

NUMA - system z niejednorodnym dostępem do sieci

CCNUMA- z zapewnieniem koherentności

Najbardziej efektywne są systemy z pamięcią rozproszoną.

Ruting: w sieci: przesyłanie komunikatów z jednego wierzchołka do drugiego.

Mapping: zagadnienie odwzorowania. Mamy przesłać P₀ - P1 - P₂ - P₃ jeden komunikat STORE-AND-FORWARD - zapamiętaj i przekaż dalej.

Czas przesyłania:

t= t_STARTU+l*t + l*m*t_B=t_S+t_m+t_B

l - liczba hops

t - t przesyłania nagłówka

m - długość słowa w bajtach

t_B - czas przesłania jednego bajtu

CUT-AND-TROUGH

t= t_s + m*t_B+(l-1) * t_m

0 ( m+l )

0 ( m )

t = t_s +m t_B

Wieloprocesorowe komp klasy PC - architektura SMP (symetryczny multiprocesor: bus-based), każdy procesor ma taki sam dostęp do pamięci

SMP wspierają: UNIX, Win NT, W2K

Athlon (k7) - zamiast magistrali jest sieć komunikacyjna, pozwala na większą liczbę połączeń

CCNUMA

Przekształcenie F - jest to macierz, bo jest to odwzorowanie liniowe

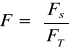
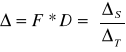
Mnożenie macierzy:

For(i=0; i<M; i++)

{ For(j=0; j<N; j++)

{ C_ij=0;

For(k=0; k<K; k++)

C_ij+=a_ik*b_kj;

}

}

n=3

K³={K=(i,j,k): 0≤i≤M-1; 0≤j≤N-1; 0≤k≤K-1;}

K³⊂Z³

0 0 1 i

D = 0 1 0 j

1 0 0 k

f₀₀ f₀₁ f₀₂

F = f₁₀ f₁₁ f₁₂ m+1 ≤ n

f₂₀ f₂₁ f₂₂ n = 3

m.= 2,1

Projekcja wzdłuż osi i

i j k

F_s = 0 0 1 detF≠0

0 1 0

Żadna kolumna nie może być=0

F_T*d_a ≥1 → f₂₁≥

F_T*d_b ≥1 → f₂₀≥

F_T*d_c ≥1 → f₂₂≥

d_a

F_T ( f₂₀ f₂₁ f₂₂ ) 0 F_T=[1,1,1]

1

0

0 0 1

F= 0 1 0

1 1 1 detF= -1

S T

K_S² Δ_S K_T¹ Δ_T

K _S² - procesory

Δ_S - połączenia pomiędzy nimi

K_T¹ - momenty pracy procesorów

Δ_T - z jaką częstotliwością poszczególne zmienne są przekazywane między procesorami

K _S²={ K _S=(k, j); 0≤k≤K-1; 0≤j≤N-1 }

Δ_S = F*D = 1 0 0

0 1 0

δ_c δ_a δ_b

K_T¹={ K_T=(t); 0≤t≤(N-1)+(M.-1)+(K-1) }

min≤t≤max

T=max-min+1 = N+M+K-2

Δ_T=F_T*D=[1,1,1]

Algorytm eliminacji Gaussa LU

A=LU /*L^-1

L^-1*A=U

MA=U A=[A*/b]

b - wektor prawych stron

A - macierz, składa się z macierzy wejściowej rozszerzonej o 1

Algorytm:

for(k=0; k<N-2; k++)

for(i=k+1; i<N; i++) //(k- kolejne kroki)

{ m_ik=a_ik/a_kk;

for(j=k+1; j<N; j++)

a_ij=a_ij-m._ik+a_kj ;

}

Na współczesnych procesorach mamy dużą ilość pamięci wirtualnej - logicznej.

Page fault - strona niedostępna

System typu SISD - sekwencyjny

Na wejściu mamy potok instrukcji (sekwencyjny), z jednego potoku robimy kilka. Dla jednego potoku wykonują się różne instrukcje równoległe.

VLIM (Very Long Instruction Word) - nowa architektura procesorów: Itanium 64 - nowy procesor

Przykład: program niezoptymalizowany.

Założenia:

1. macierze o rozmiarze 1024×1024 - 1 mln słów

2. strona pamięci wirtualnej zawiera 65536 słów

3. jedna macierz wymaga 16 stron

4. dostępna pamięć RAM odpowiada 16 stronom - 1 mln słów

5. w przypadku sekwencyjnego dostępu do kolumn, oznacza to wystąpienie jednego „page fault” po każdych 64 kolumnach

Inner product approach -ijk

DO 30 I=1, N

DO 20 J=1,N

DO 10 K=1,N

C(I,J)=A(I,K)*B(K,J)+C(I,J)

10 CONTINUE

20 CONTINUE

30 CONTINUE

page faults: 1 mln*16=16 mln

I/O: 16 mln*0,5sek→około 93 dni

Dla jednego elementu C(I,J) trzeba mieć dostęp do całego wiersza macierzy A. Pamięć jest zapisywana według kolumn. Dlatego gdy odczytujemy nazwę kolumny aby otrzymywać kolejną pozycję wiersza i trzeba przeskoczyć przez 16 stron i dlatego mamy 16 mln błędów (to nie są tak naprawdę błędy tylko momenty doładowania kolejnej strony z pamięci zew).

Program z zamienionymi pętlami:

Column- wise update of C - jik

DO 30 J=1, N

DO 20 K=1,N

DO 10 I=1,N

C(I,J)=A(I,K)*B(K,J)+C(I,J)

10 CONTINUE

20 CONTINUE

30 CONTINUE

macierz A: 1024*16 „page faults”

macierz B: 16 „page faults”

macierz C: 16 „page faults“

czas: 2,5 godziny

dwie wew pętle K,I obliczają wektor.

Algorytm blokowy:

Partitioning the matrices into block-columns - bloked jik

DO 40 J=1, N, NB

DO 30 K=1,N, NB

DO 20 JJ=J,J+NB-1

DO 10 KK=K,K+NB-1

C(:,JJ)=C(:,JJ)+A(:,KK)*B(KK,JJ)

10 CONTINUE

20 CONTINUE

30 CONTINUE

40 CONTINUE

macierze podzielone na bloki 256×256 tj. NB=256

macierz A: 4*16 „page faults”

macierz B: 16 „page faults”

macierz C: 16 „page faults“

razem 96 „page faults“→70 sek I/O

ATLAS (Automatically Tuned Linear Algebra Software)

Aby otrzymać blok macierzy C:

Mamy:

Program:

DO J=, N, NB

Bwork = ALPHA*B(:,J+NB-1)

DO I=1, M, NB

IF (PARTAL_MATRIX) Awork=A (I:I+NB-1,:)

Cwork(1:NB,1 :NB)=0

DO K=1, K ,NB

ON_CHIP_MATMUL(Awork,Bwork,Cwork)

END DO

C(I:I + NB -1,J:J +NB -1)=BETA*Cwork

END DO

END DO

Odwzorowanie prac na procesory

Zbiór zadań (prac) T={t₁...t_n}.

Każde zadanie ma pracochłonność t_iW_i

W_i - złożoność, pracochłonność

Zadania trzeba przydzielić do czasu i przestrzeni do zbiorów procesorów.

P=(p₁,p₂...p_m.) P- zbiór procesorów

Do każdego zadania trzeba przydzielić

t_i -> {p_i, _i p_i - procesor

_i - moment rozpoczęcia tej pracy, bo zakładamy, że zadania są niepodzielne

szukamy sposobu optymalnego - musi być zadana funkcja celu

W sposób optymalny:

Dany: zbiór T, P zbiór procesorów

Znaleźć: uszeregowanie S - odwzorowanie zbiorów zadań F w zbór procesorów, czyli zbiór momentów czasowych

S:T -> P x  (iloczyn kartezjański)

Minimalny czas realizacji algorytmu min 

Dane: Zbiór T i maks. wartość  . (czas realizacji algorytmu jest ograniczony)

Znaleźć: zbiór procesorów o minimalnym koszcie

Kolejna prace z listy prac przydzielamy do pierwszego wolnego procesora na liście

Nie istnieje algorytm optymalny w czasie będącego funkcją wielomianowej:

Nie ma czasu n^x , jest czas xⁿ

PROGRAMOWANIE WSPÓŁBIEŻNE:

PROCES-program sekwencyjny w trakcie wykonywania

DWA PROCESY WSPÓŁBIEŻNE-jeżeli jeden z nich rozpoczyna się przed zakończeniem drugiego.

Będą nas interesować jedynie takie procesy, których wykonania są od siebie uzależnione przy czym uzależnienie wynika z faktu, że

procesy są sobą WSPÓŁPRACUJĄ lub między sobą WSPÓŁZAWODNICZĄ.

KOMUNIKACJA I SYNCHRONIZACJA:

Współpraca wymaga od procesów komunikowania się. Akcje komunikujących się procesów muszą być częściowo uporządkowane w czasie, ponieważ informacja musi najpierw zostać utworzona zanim zostanie wykonana. Takie porządkowanie w czasie

różnych procesów nazywa się SYNCHRONIZACJĄ.

Współzawodnictwo także wymaga synchronizacji: - akcja procesu musi być wstrzymana jeżeli zasób potrzebny do jej wykonania jest w danej chwili zajęty przez inny proces.

PROGRAM WSPÓŁBIEŻNY jest zbiorem procesów (wątków)

PROBLEMY WZAJEMNEGO WYKLUCZANIA:- w teorii procesów współbieżnych wspólny obiekt, z którego może korzystać w sposób wyłączny wiele procesów np. (łazienka, koszyk w sklepie) nazywa się ZASOBEM DZIELONYM, natomiast fragment procesu, w którym korzysta on z obiektu dzielonego (mycie się, zakup) nazywa się SELEKCJĄ KRYTYCZNĄ.

-Problem wzajemnego wykluczania definiuje się następująco:

zsynchronizować N procesów, z których każdy w nieskończonej pętli na przemian zajmuje się WŁASNYMI SPRAWAMI i wykonuje sekcje krytyczną, w taki sposób, aby wykonanie sekcji krytycznych jakichkolwiek dwóch lub więcej procesów nie pokrywało się w czasie.

Aby ten problem rozwiązać, należy do treści tego procesu, wprowadzić dodatkowe instrukcje poprzedzające sekcję krytyczną (nazywa się PROTOKOŁEM WSTĘPNYM)

i instrukcje następują bezpośrednio po sekcji krytycznej (zwane PROTOKOŁEM KONCOWYM).

PRZYKŁAD PROBLEMY WZAJEMNEGO WYKLUCZANIA:

-MULTIPROCESOR czyli system równoległy z pamięcią wspólną

-dwa procesy współbieżne, z których jeden realizuje operacje x=x+1, a drugi x=x+2

-każda z powyższych operacji realizowana jest za pomocą trzech operacji maszynowych tj.(i)load x, (ii)add(1 lub 2), (iii)store x

przypuśćmy, że x=5, wówczas jeden z możliwych scenariuszy wygląda następująco:

1.Pierwszy proces pobiera swoja kopię x:x=5,

2.Pierwszy proces oblicza x=x+1 (lecz wartość, wynikowa nie zostaje jeszcze zapisana do pamięci wspólnej),

3.Drugi proces oblicza włącza się do akcji pobierając swoją kopię x:x=5,

4.Drugi proces oblicza x=x+2:x=7, nie zapisuje wyniku do pamięci wspólnej,

5.Pierwszy proces zapisuje swój wynik x=6 do pamięci,

6.Drugi proces zapisuje swój wynik x=7 do pamięci wspólnej.

Wniosek: otrzymujemy x=7 zamiast prawidłowego wyniku x=8.

Blokada i zagłodzenia

-w poprawnym programie współbieżnym tj. posiadającym własność żywotności, w każdym procesie powinno w końcu nastąpić oczekiwane zadanie.

-w niepoprawnym programie mogą wystąpić zjawiska blokady lub zagłodzenia

-zbiór procesów znajduje się w stanie blokady jeżeli każdy z tych procesów jest wstrzy-

mywany w oczekiwaniu na zdarzenie które może być spowodowane tylko przez jakiś inny proces z tego zbioru.

-inna nazwa zjawiska blokady to zastój, zakleszczenie lub martwy punkt

-specyficznym przypadkiem nieskończonego wstrzymywania procesu jest zjawisko zagłodzenia zwane także wykluczeniem

-jeżeli sygnał synchronizacyjny może być

odebrany tylko przez jeden z oczekujących nań procesów powstaje problem, który z procesów wybrać

Mechanizm synchronizacji

-nisko poziomowe: w jęz. niskiego poziomu÷przerywanie

-wysoko poziomowe: dostępne w jęz. wysokiego poziomu

Semafory

Semafor to abstrakcyjny typ danych, na którym oprócz określenia jego stanu początkowego można wykonywać tylko dwie operacje umożliwiające wstrzymywanie procesów a mianowicie:

-opuszczanie semafora

-podniesienie semafora

o których zakłada się, że są niepodzielne, co

oznacza, że w danej chwili może być wykonywana tylko jedna z nich.

Semafor binarny

Def. Klasyczna

-opuszczenie semafora binarnego to wykonanie instrukcji PB(S):

czekaj aż s==1; s=0

-podniesienie semafora binarnego VB(S):

s=1

Def. Praktyczna:

-opuszczenie semafora binarnego PB(S):

jeżeli s==1, to s=0, w przeciwnym razie wstrzymaj działanie procesu wykonującego tę operację

-podniesienie semafora binarnego VB(S):

jeżeli są procesy wstrzymane w wyniku wykonania operacji opuszczenia semafora s to wznów jeden z nich,w przeciwnym razie s=1

Semafor ogólny:

Def. Praktyczna - opószczeniue semafora ogólnego P(S): jeżeli S>0 to S=S-1, w przeciwnym razie wstrzymaj działanie procesu wykonującego tą operację; Podniesienie semafora binarnego V(S): jeżeli są procesy wstrzymane w wyniku wykonania operacji opuszczania semafora S, to zwarty jeden z nich, w przeciwnym razie S=S+1

Definiowanie zmiennych semaforowych w programach.

Semafor ogólny: semaphore sem=4;

Semafor binarny: binary semaphore=1;

Przykłady programów współbieżnych z wykorzystaniem semaforów:

Wzajemne wykluczenia:

Int n=1;

Binary semaphore s=1;

Proces P(int i);

{while {true}

{własne sprawy;

PB(s);

Sekcja krytyczna;

VB(s);

}

} Problem pięciu filozofów.

Rozwiązanie z możliwością blokady

Binary semaphore widelec[5]={1,1,1,1,1};

Proces filozof(int i)

{while {true}

{PB(widelec[i]);

PB(widelec[(i+1)%5]);

Jedzenie;

VB(widelec[i]);

VB(widelec[i+1)%5]);

}

}

Rozwiązanie porawne:

Binary semaphore widelec[5]={1,1,1,1,1};

Semaphore lokaj=4;

Proces filozof(int i)

{while {true}

{myślenie;

P(lokaj);

PB(widelec[i];

PB(widelec[(i+1)%5]);

Jedzenie;

VB(widelec[i]);

VB(widelec[(i+1)%5]);

V(lokaj);

}

}

C

M

C₃₂

N

K

B₂₃

B₂₂

B₁₂

A₃₁

M

A

A₃₂

A₃₃

K

B

N

×

---