AKADEMIA BYDGOSKA
im. Kazimierza Wielkiego
Wydział Matematyki ,Techniki i Nauk Przyrodniczych
FIZYKA - LABORATORIUM
Temat: Badanie drgań tłumionych wahadła torsyjnego.
Wykonali:
Jacek Strauhs
Marcin Szyszko
Bydgoszcz 2003
1. Cześć teoretyczna
Ruchem harmonijnym nazywamy ruch odbywający się pod wpływem siły F, wprost proporcjonalny do wychylenia x i przeciwnie do niej skierowany.
F = -kx ; k oznacza współczynnik sprężystości.
Rozwiązanie tego równania ma postać:
Wykorzystując II zasadę dynamiki Newtona równanie ruchu możemy zapisać jako:
w którym A oznacza amplitudę (jest ona w przypadku drgań nie tłumionych stała), ω0 oznacza częstość kątowa a ϕ jest stałą fazową.
Drgania odbywane w warunkach rzeczywistych w dowolnym ośrodku materialnym zawsze są połączone z przekazywaniem energii otoczeniu w związku z pokonywaniem sił oporu. W wyniku wykonywanej pracy energia ciała drgającego maleje i zmniejsza się amplituda drgań. Takie drgania nazywamy tłumionymi ( gasnącymi, zanikającymi).
Siła hamująca F1 jest proporcjonalna do prędkości v i skierowana do niej przeciwnie:
F1 = -b*v =-b*(dx/dt); b oznacza współczynnik proporcjonalności zwany współczynnikiem
oporu.
Równanie ruchu ciała o masie m wykazującego drgania harmoniczne tłumione ma postać:
Z powyższego równania wynika, że amplituda A drgań tłumionych zmienia się wykładniczo z biegiem czasu przyjmując wartość zerową teoretycznie po czasie nieskończenie długim.
Niech A1 oznacza amplitudę w chwili t, zaś An amplitudę po upływie czasu t+nT, gdzie nT oznacza czas równy n okresom T.
Możemy zapisać:
Dzieląc powyższe równania stronami otrzymujemy:
stąd wyliczamy stałą tłumienia:
2. Badanie drgań tłumionych wahadła w cieczy.
Lp. |
Wychylenie lewe xnl [cm] |
Wychylenie prawe xnp [cm] |
Amplituda An [cm] |
1 |
2 |
35,5 |
16,75 |
2 |
3,7 |
34,9 |
15,6 |
3 |
5 |
34 |
14,5 |
4 |
6 |
33,2 |
13,6 |
5 |
7 |
32,3 |
12,65 |
6 |
8 |
31,5 |
11,75 |
7 |
9 |
31 |
11 |
8 |
10 |
30 |
10 |
9 |
11,1 |
29,5 |
9,2 |
10 |
11,6 |
28,7 |
8,55 |
Z wykresu wynika, że najlepiej wziąć punkty A6 i A7
Suma 10 okresów: 67 s. Średni czas trwania okresu: 6,7[s]
![]()
![]()
Dokładności pomiaru: ΔA6=0,5 [m]; ΔA7=0,5 [m]; ΔT=0,01 [s]
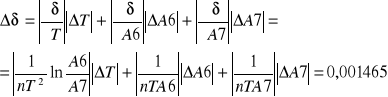
Wyszukiwarka