Zad.1. Wpływy do budżetu z cła pobranego przez Izby Celne w Polsce w latach 1997-2005 w mld zł wynosiły:

Lata	Cło w mld zł
1997	7,0
1998	6,1
1999	5,3
2000	5,1
2001	4,1
2002	3,8
2003	3,8
2004	2,3
2005	1,3

1. Wpływy z cła przedstawiono w szeregu czasowym: ၿ momentów ၿ okresów; wykazują tendencję: ၿ rosnącą ၿ stagnację ၿ malejącą, ponieważ ................................................................

2. Podać wartość i interpretację obu parametrów liniowej funkcji trendu.

3. Podać wartość i interpretację odchylenia standardowego reszt.

4. Funkcja trendu liniowego jest: ၿ źle ၿ umiarkowanie ၿ dobrze dopasowana do danych empirycznych, ponieważ:

1. ................................................................................................

2. ...............................................................................................

5. Przyjąć założenie, że dotychczasowa tendencja nie ulegnie zmianie i oszacować wpływy z cła w 2006 roku. Uwzględnić średni błąd szacunku.

6. Podać interpretację parametru b następującej funkcji trendu
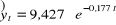
   , dla której wariancja resztowa wynosi 0,4571 (mld zł)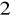
   , a współczynnik indeterminacji 0,1245.

7. Która z funkcji trendu: ၿ z pkt. 2, czy ၿ z pkt. 6 jest gorsza i dlaczego?

1. ................................................................................................

2. ................................................................................................

Zad. 2. Dynamikę liczby osób z wykształceniem podstawowym, zatrudnionych w NBP w Polsce (stan w dniu 31 XII) opisuje ciąg indeksów:

Lata	2002	2003	2004	2005	2006
Rok pop. = 100	-	68,60	91,06	79,86	97,03

1. Podano indeksy: indywidualne agregatowe jednopodstawowe łańcuchowe

2. Z roku na rok następuje: wzrost spadek liczby osób z wykształceniem podstawowym.

3. W ostatnich latach tempo spadku wzrostu było coraz większe mniejsze stałe zmienne.

4. Najmniejsza liczba osób z wykształceniem podstawowym była w roku ................................................

5. Największe tempo spadku wystąpiło w roku ................................. Zinterpretować przedstawiony indeks dla tego roku.

6. Obliczyć i zinterpretować średnie tempo spadku wzrostu liczby osób z wykształceniem podstawowym.

7. Obliczyć indeksy względem 2002 roku. Zinterpretować obliczony indeks dla 2005 roku.

8. W 2004 roku liczba osób z wykształceniem podstawowym wynosiła 591. Obliczyć liczbę osób z wykształceniem podstawowym w 2006 roku.

Zad.3. Zależność między poziomem obrotów w tys. zł (x) a kosztami transportu w tys. zł w 26 losowo wybranych przedsiębiorstwach opisuje następująca funkcja regresji:
, dla której
,
.

1. Podać wartość i interpretację współczynnika regresji.

2. Podać wartość i interpretację współczynnika determinacji.

3. Podać wartość i interpretację przeciętnego błędu szacunku.

4. Podać wartość i interpretację współczynnika korelacji liniowej Pearsona.

5. Jakiej wysokości kosztów należy się spodziewać w przedsiębiorstwie, w którym obroty wynosiły 600 tys. zł?

Zad.1. W losowo wybranych gospodarstwach domowych zbadano zależność między miesięcznym dochodem (w tys. zł ) a poziomem wydatków na artykuły zbożowe (w zł na 1 osobę). Otrzymano:

Dochód (tys. zł)	Wydatki (zł/os)
0,8	95
1,0	93
1,2	85
1,2	90
1,3	83
1,5	83
2,0	70
2,2	65

1. Między dochodem i wydatkami na artykuły zbożowe występuje zależność  dodatnia  ujemna, ponieważ .............................

2. Podać wartość i interpretację współczynnika korelacji liniowej Pearsona.

3. Podać wartość i interpretację współczynnika regresji.

4. Podać wartość i interpretację odchylenia standardowego reszt.

5. Wyznaczona funkcja regresji jest:  źle  umiarkowanie  dobrze dopasowana do danych empirycznych, ponieważ:

1. ................................................................................................

2. ...............................................................................................

6. Oszacować poziom wydatków przy dochodzie wynoszącym 2,5 tys. zł. Uwzględnić średni błąd szacunku.

7. Podać interpretację parametru b następującej funkcji regresji
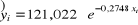
   , dla której wariancja resztowa wynosi 5,14499 (zł/osobę)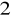
   , a współczynnik indeterminacji 0,0391.

8. Która z funkcji regresji:  z pkt. 3, czy  z pkt. 7 jest lepsza i dlaczego?

1. ................................................................................................

2. ................................................................................................

Zad. 2. Dynamikę wypadków drogowych spowodowanych przez pijanych kierowców w Polsce opisuje ciąg indeksów:

Lata	2000	2001	2002	2003	2004	2005	2006	2007	2008
Rok 2000 = 1	1	0,79	0,87	0,75	0,75	0,77	0,69	0,65	0,67

1. Podano indeksy: indywidualne agregatowe jednopodstawowe łańcuchowe

2. W tym szeregu występuje tendencja rosnąca stagnacja zmienna w czasie malejąca

3. Największa liczba wypadków była w roku .................................................

4. Obliczyć indeksy z roku na rok. Zinterpretować obliczony indeks dla 2008 roku.

5. W ostatnich latach tempo: spadku wzrostu było coraz: większe mniejsze stałe zmienne.

6. Największe tempo spadku wystąpiło w roku ..................... Zinterpretować obliczony indeks dla tego roku.

7. Obliczyć i zinterpretować średnie tempo spadku wzrostu liczby wypadków.

8. W 2003 roku liczba wypadków spowodowanych przez pijanych kierowców wynosiła 3,9 tys. Obliczyć liczbę wypadków w 2000 roku.

Zad.3. Dynamikę przewozów pewnej firmy transportowej w tys. ton opisuje funkcja trendu:
(gdzie
dla II kwartału 2004 roku). Wskaźniki sezonowości wynosiły:
,
,
. Wariancja resztowa wynosiła 9(tys. ton)².

1. Podać interpretację współczynnika zmian w czasie

2. Podać wartość i interpretację wskaźnika sezonowości dla trzeciego kwartału.

3. Określić rodzaj przedstawionych wskaźników sezonowości……………………….. Suma tych wskaźników powinna wynosić .........................

4. Zakładając, ze dotychczasowa tendencja nie ulegnie zmianie oszacować poziom przewozów w trzecim kwartale 2006 roku.

4

---