EAiE 1. Gerard Kaduczek
2. Krzysztof Korbel ROK I GRUPA III ZESPÓŁ XI
Pracownia fizyczna Temat: Wahadło fizyczne. Nr ćwiczenia:
1
Data wykonania:
11.04.97 Data oddania:
18.04.97 Zwrot do popr.
Data oddania:
Data zaliczenia:
OCENA:
I. Cel ćwiczenia:
Zapoznanie się z ruchem drgającym wahadła fizycznego. Wyznaczenie momentu bezwładności brył sztywnych poprzez pomiar okresu drgań.
II. Opracowanie teoretyczne:
Bryłę sztywną można traktować jako ciągły zbiór punktów materialnych o różnych odległościach od osi obrotu. Moment bezwładności wyraża się zatem wzorem:
I = ![]()
W szczególności dla punktu materialnego:
I = m . r2
Każdą bryłę o masie m, zawieszoną w punkcie O różnym od środka ciężkości można uważać za wahadło fizyczne. Podczas ruchu drgającego mamy do czynienia z obrotem bryły sztywnej wokół osi O pod wpływem momentu siły ciężkości, który dla wychylenia wynosi:
M = m . g . a . sin
Ruch wahadła opisuje również druga zasada dynamiki dla ruchu obrotowego, która po połączeniu z poprzednim wzorem daje:
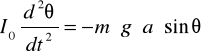
Znak minus uwzględnia fakt, że siła m.g.a.sin jest zawsze skierowana przeciwnie do kierunku wychylenia.
Przy małym kącie wychylenia sin = , więc otrzymujemy:
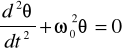
gdzie: ![]()
Po rozwiązaniu równania różniczkowego otrzymujemy wzór na ruch harmoniczny prosty:
= mcos(0 + )
Amplituda i faza początkowa zależą od warunków początkowych.
Okres drgań T, związany bezpośrednio z częstością wynosi:
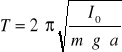
Występujący powyżej moment Jo, jest momentem bezwładności względem osi obrotu przechodzącej przez punkt zawieszenia O. Jeżeli przez Is oznaczymy moment bezwładności względem środka ciężkości S. To związek pomiędzy Io i Is jest dany przez twierdzenie Steiner'a:
Io = Is + m . a2
III. Wyniki pomiarów.
Dla wszystkich wielkości wykonano kilka pomiarów, z których wyliczono medianę (patrz: oryginalne wyniki pomiarów).
Pręt.
Do wyznaczenia wymiarów pręta użyliśmy przymiaru milimetrowego, za pomocą którego zmierzyliśmy długość pręta (l), a następnie odległość od punktu zawieszenia do końca pręta (b).
Odległość od punktu zawieszenia do środka pręta (a):
a = 0.5 . l - b
Pierścień.
Do pomiaru średnicy pierścienia (d) oraz głębokości wcięcia (w) użyliśmy przymiaru milimetrowego, natomiast do pomiaru grubości (c) wykorzystaliśmy suwmiarkę.
Zewnętrzny promień pierścienia: Rz = d / 2
Wewnętrzny promień pierścienia: Rw = d / 2 -c
Odległość od punktu zawieszenia do środka pierścienia: a = Rw + w
tabela pomiarowa I
obiekt m
[kg] l
[m] d
[m] a
[mm] b
[mm] c
[mm] w
[mm] Rw
[mm] Rz
[mm]
pręt I 0,75410-3 0,7983.10-3 - 299.87 99,13 - - - -
pręt II 0,66910-3 0,7493.10-3 - 274,90 99,60 - - - -
pierścień I 1,38010-3 - 0,35642.10-4 166,09 - 15,21 3.09 163 178,21
pierścień II 1,11610-3 - 0,35062.10-4 161.68 - 14,76 1,14 160,54 175,3
Wyniki 10 pomiarów czasu liczonego w [s] 30 wahnięć wahadła fizycznego dla wychyleń początkowych nie przekraczających kilku stopni:
tabela pomiarowa II
obiekt 1 2 3 4 5 6 7 8 9 10
pręt I 41,47 41,53 41,60 41,41 41,56 41,53 41,55 41,52 41,58 41,50
pręt II 40,09 40,15 40,10 40,16 40,18 40,09 40,12 40,13 40,16 40,15
pierścień I 32,84 32,53 32,72 32,71 32,60 32,75 32,59 32,68 32,70 32,72
pierścień II 32,72 32,69 32,68 32,68 32,72 32,75 32,66 32,67 32,68 32,70
IV. Opracowanie wyników.
1. Liczymy średni czas n wahnięć i odchylenie standardowe średniej według wzorów:
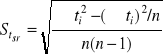
![]()
Natomiast średni okres drgań wahadła i jego błąd według wzorów:
![]()
![]()
,
gdzie błąd okresu wynika z prawa przenoszenia błędów. Mówi ono, że dla wielkości fizycznej zależnej od kilku innych: y = f(x1,...,xk,...) błąd y wyraża się wzorem:
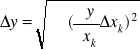
tabela obliczeniowa I
obiekt tśr
[s] Tśr
[s] Tśr
[s] Stśr
10-2 [s] tśr
[s]
pręt I 41,525 1,384 0,001 2,413 0,03
pręt II 40,133 1,338 0,001 2,106 0,03
pierścień I 32,684 1,089 0,001 2,016 0,03
pierścień II 32,695 1,090 0,001 2,017 0,03
2. Liczymy momenty bezwładności względem osi obrotu i ich błędy (zgodnie z ww. prawem przenoszenia) według wzorów:
![]()
![]()
3. Liczymy momenty bezwładności względem środka ciężkości z twierdzenia Steinera ,a także błędy tych wielkości na podstawie prawa przenoszenia błędów:
Io = Is + m.a2 Is = Io - m.a2
tabela obliczeniowa II
obiekt I0 I0 Is Is
pręt I 0,1063 0,0006 0,0405 0,0007
pręt II 0,0821 0,0005 0,0316 0,0005
pierścień I 0,0676 0,0004 0,0295 0,0005
pierścień II 0,0589 0,0004 0,0251 0,0005
4. Liczymy momenty bezwładności względem środka ciężkości na podstawie zmierzonych wartości masy i wymiarów geometrycznych (oraz ich błędy zgodnie z prawem przenoszenia):
Pręt:
![]()
![]()
Pierścień:
![]()
![]()
tabela obliczeniowa III
obiekt Is Is
pręt I 0,0400 0,0003
pręt II 0,0313 0,0003
pierścień I 0,0402 0,0003
pierścień II 0,0315 0,0003
V. Ocena błędów.
Porównując wartości momentów bezwładności względem środka ciężkości (liczonych na podstawie zmierzonego okresu drgań oraz na podstawie wymiarów geometrycznych) zauważamy, że mieszczą się one w granicach błędów. W przypadku pierścienia wyniki nieco się różnią. Prawdopodobnie został popełniony błąd podczas mierzenia czasu 30 wahnięć tego obiektu (ten wariant można opuścić), albo trzeba było wykonać więcej wahnięć np. 100, co dało by pewność, że nie popełniliśmy błędu podczas tego pomiaru. W przypadku pomiaru Is dla prętów wynik jest niewiarygodnie podobny (patrz tabela obliczeniowa I i II).
VI. Wnioski.
1. Błąd T ma największy wpływ na błąd wyniku momentu bezwładności ze względu na to, że T występuje we wzorze w drugiej potędze.
2. Wartość momentu bezwładności zależy wprostproporcionalnie od masy.
VII. Załączniki:
Oryginalne wyniki pomiarów.
Wyszukiwarka