Przebieg doświadczenia

Zmontowałem układ z cewką zgodnie z rysunkiem umieszczonym w opisie doświadczenia. W układzie tym cewka nie byłe podłączona cała lecz tylko jej część oznaczona zaciskami 0 1. Następnie za pomocą autotransformatora zmieniałem wartość napięcia prądu i na woltomierzu i amperomierzu odczytywałem wartości. Dla układu z kondensatorami wpiąłem odpowiednio woltomierz i przeprowadziłem serie identycznych pomiarów jak dla cewki. W układzie sprawdzałem charakterystyki prądowo napięciowe dla trzech różnych pojemności. Najpierw użyłem jednego kondensatora później dwóch i trzech połączonych szeregowo.

W schemacie trzecim badałem układ zmontowany z wcześniej badanej cewki oraz z pojedynczego kondensatora.

Opracowanie wyników pomiaru

Wpierw zajmuję się obwodem w której badałem samą cewkę. Po narysowaniu charakterystyki prądowo napięciowej obliczam z wykresu wartość zawady. Po przybliżeniu krzywą trendu punktów pomiarowych komputer obliczył wzór na otrzymaną prostą, który ma postać I=0,01U. Zawada cewki to ctgα α- kąt zawarty między otrzymaną prostą, a osią U. Ctgα=1/tgα a wartość tgα jest współczynnikiem kierunkowym otrzymanej prostej, czyli tgα=0,01. W takim razie :

ctgα=1/0,01=100

Zawada badanej części cewki wynosi zatem Z=100Ω

Jak podano w opisie do doświadczenia oporność części badanej cewki ma zaciskach 0-1 wynosi R=30Ω. Korzystając ze wzoru
mogę obliczyć oporność indukcyjną cewki i wynosi ona
. Po podstawieniu otrzymanych wartości liczbowych X_L=95,4Ω.

Prąd wykorzystywany w doświadczeniu ma częstotliwość f=50Hz, a zatem ω wykorzystywane w doświadczeniu wynosi ω=2*50*π=50*3,14=314Hz.

Posiadają wartość oporności indukcyjnej cewki oraz wartość częstości mogę obliczyć indukcyjność użytej części cewki. X_L=ωL, zatem
=0,30H

W analogiczny sposób przeprowadzam obliczenia dla układu składającego się z pojemności. Układ I zawiera jeden kondensator, układ II dwa kondensatory, a układ III zawiera trzy kondensatory połączone szeregowo.

Obliczam wartość zawady z otrzymanego wykresu:

	ctgα	tgα	Zawada Z [Ω]
I	0,0011	909	909
II	0,0006	1666	1666
III	0,0004	2500	2500

Ponieważ badane kondensatory były jednakowe i połączyłem je szeregowo to pojemności dla odpowiednich układów wynoszą:

	Pojemności[F]
I	4*10^-6
II	2*10^-6
II	(4/3)*10^-6

Teraz mogę obliczyć oporność pojemnościową kondensatorów

	XC[Ω]
I	788
II	1592
III	2388

W przypadku wszystkich trzech układów kondensatorów możemy zauważyć na wykresie, że spełniają one prawo Ohma. Zależność natężenia od przyłożonego napięcia wyszła liniowa, zatem wartość zawody wyszła stała. W przypadku szeregowego połączenia kondensatorów widzimy, że im większa pojemność tym mniejsza jest zawada układu.

Dla układu złożonego z cewki oraz z jednego kondensatora połączonych szeregowo zawada obliczona z wykresu wynosi :

ctgα=0,0012 tgα=1/0,0012=833,3 Z=833,3Ω

Natomiast zawada obliczona ze wzoru :

=693,3Ω

Ocena błędów

Aby obliczyć błąd dla zawady najpierw muszę wiedzieć jaki jest błąd dla przyrządów pomiarowych. Napięcie prądu było badane za pomocą miernika elektrycznego. Jego dokładność przyjmuję równą 0,001V gdyż z taką dokładnością można było na nim odczytywać wyniki. Pomiar natężenia był dokonywany za pomocą miernika wskazówkowego o klasie dokładności 4,0. Pomiarów dokonywałem w trzech zakresach 60mA, 15mA, 3mA. Błąd obliczam ze wzoru:

Zakres	ΔI[A]
60*10^-3	0,0024
15*10^-3	0,0006
6*10^-3	0,00024

Na wykresie udało mi się zaznaczyć tylko błąd pomiarowy dla natężenia, dla napięcia był on za mały, żeby można go było zarysować.

Błąd dla zawady ΔZ obliczam z prawa Ohma I=U/Z za pomocą różniczki zupełnej.

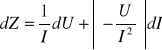
Obliczony błąd zawady tą metodą znajduje się na końcu sprawozdania w tabelce z wynikami.

Natomiast błąd dla indukcyjności obliczam ze wzoru:

Wnioski

Dla układu RLC zawadę liczyłem dwoma sposobami. Pierwszym sposobem było po narysowaniu punktów pomiarowych na wykresie obliczenie wzoru krzywej regresyjnej tych punktów. Następnie policzyłem z zależności trygonometrycznych odpowiednie kąty tak jak to napisałem wyżej. Przyglądając się bliżej tej metodzie można zauważyć, że tak naprawdę jest to tylko prawo Ohma policzone jako wartość średnia dla wszystkich punktów jednocześnie. Druga metoda bazuje na obliczeniu zawady za pomocą wcześniej wyliczonych wartości takich jak oporność pojemnościowa i oporność indukcyjna. Pierwszą metodą wynik wynosi Z=833,3Ω za pomocą drugiej metody zawada wynosi Z=693,3Ω. Jak widzimy rozbieżność między metodą pierwszą a drugą wynosi około 16,8%. W tym przypadku rozbieżność nie jest aż tak duża. Jednak w tym jak i w innych pomiarach ewentualnym źródłem błędu mógł być błąd paralaksy. Błędem jest też obciążony wykonany przez mnie wykres oraz krzywa regresyjna. Rysując tą krzywą brałem pod uwagę aby zaczynała się ona w początku układu współrzędnych, czyli aby przy zerowym napięciu nie było żadnego oporu. Krzywa od razu uległa niewielkiemu skręceniu w prawo co spowodowało zwiększenie ctgα a więc zwiększenie zawady obliczonej tą metodą.

Teraz zajmę się ogólnym błędem liczony metodą różniczki zupełnej. Dla zawady widzimy, że małych wartości natężenia błąd dla zawady jest duży w stosunku do samej wartości tej zawady. Patrząc na wzór niepewności pomiarowej zawady widzimy, iż w mianowniku pojawia się wyrażenie 1/I². Dla małych wartości natężenia prądu wyrażenie to zamienia się w bardzo dużą wartość liczbową. Dlatego też błąd zawady dla niewielkich wartości natężenia prądu jest bardzo duży.

Z analogicznych przyczyn błąd dla indukcyjności jest również w przypadku małych natężeń bardzo duży w stosunku do wartości obliczonej.

Z tych powodów wynika, że jeśli chcemy uzyskać pomiary o dużej dokładności i małych błędach pomiarowych musimy badać obwód dla dużych, stosunkowo dużych natężeniach prądu.

---